Приклад аналізу та висновків до задачі.

Дата: 2025-06-02; Просмотры: 9
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Задача. Маємо вибірку даних, які характеризують роботу підприємства. Побудувати парну лінійну регресійну модель залежності об’єму реалізації підприємства (Y), тис. грн. від витрат на впровадження інновацій в попередньому періоді (Х), тис грн. виду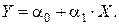

Для аналізу необхідно розрахувати: коефіцієнт детермінації; коефіцієнт кореляції, F-критерій Фішера; стандартні похибки оцінок параметрів моделі порівняти з величиною оцінок; перевірити значущість коефіцієнта детермінації, коефіцієнта кореляції та оцінок параметрів моделі; знайти інтервали надійності для оцінок параметрів моделі.

Знайти прогнозне значення залежної змінної Yпр, яке відповідає очікуваному значенню незалежної змінної Xпр.

Відобразити модель на графіку.

Зробити економічний висновок.

Вихідні дані для розрахунку в табл. 2.1.

Таблиця 2.1

Спостереження Об’єм реалізації, тис. грн. Витрати на впровадження інновацій в попередньому періоді, тис. грн.
  Y Х
1 862,3 27,1
2 804,9 25,2
3 804,9 25,0
4 559,5 14,3
5 592,3 14,2
6 583,1 11,5
7 832,1 24,3
8 851,7 21,5
Середнє значення 736,35  

 

Для спрощення розрахунків використаємо статистичну функцію Microsoft Excel ЛИНЕЙН.

Ця функція для визначення оцінок параметрів лінійної регресії застосовує метод найменших квадратів.

Суть методу найменших квадратів, полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається, (Xi, Yi) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою

 

 

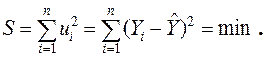Результат застосування статистичної функції ЛИНЕЙН – це оцінка параметрів лінійної регресії та регресійна статистика:

Статистична функція ЛИНЕЙН обчислює до­даткову регресійну статистику:

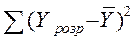– сума квадратів відхилення, що пояснюється регресією (колонка 5 з таблиці 2.2);

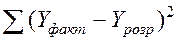– сума квадратів відхилення, що пояснюється похибкою u (колонка 3 з таблиці 2.2);

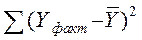– загальну суму квадратів відхилень (колонка 4 таблиці 2.2).

 

20,45

319,44
3,033

64,203
0,883

48,935
45,47

6
108879,7

14367,5

a0 = 319,44; a1 = 20,45

Можна побудувати рівняння регресії: Yрозр = 319,44 + 20,45 × Х.

Коефіцієнт регресії a1 = 20,45 говорить про те, що збільшення витрат на впровадження інновацій на 1 тис. грн. збільшить об’єм реалізації на 20,45 тис. грн.

Для визначення статистичних коефіцієнтів та подальших розрахунків знаходимо відхилення (табл. 2.2).

Таблиця 2.2

Yфакт

Yрозр

 (Yфакт – Yрозр)2 (Yфакт – Yсер)2 (Yрозр – Yсер)2
1

2

 3 4 5
862,3

873,62

 128,05 15863,403 18843,05
804,9

834,76

 891,76 4699,1025 9685,00
804,9

830,67

 664,22 4699,1025 8896,74
559,5

611,86

 2742,07 31275,923 15496,58
592,3

609,82

 306,94 20750,403 16009,89
583,1

554,61

 811,87 23485,563 33030,65
832,1

816,36

 247,81 9168,0625 6401,28
851,7

759,10

 8574,78 13305,623 517,56
 

 

 14367,5 123247,18 108879,7

Коефіцієнт детермінації

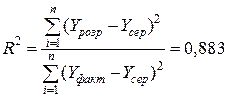(2.1)

коефіцієнт кореляції

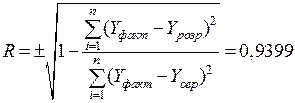(2.2)

Іноді для спрощення розрахунків тісноту кореляційного зв'язку характеризують коефіцієнтом кореляції, який розраховується за формулою:

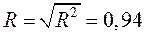(2.3)

F-критерій Фішера

Тестування значимості змінної Х, або адекватності моделі проводиться за критерієм Фішера.

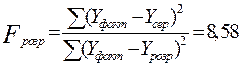(2.4)

Fрозр = 8,58

F0,05табл визначаємо за допомогою статистичної функції Microsoft Excel FРАСПОБР(0,05;6;7) для рівня надійності a=0,05 і ступенів вільності відповідно f1 = (n–m–1) = 8–1–1=6 та f2 = (n–1)= 8–1=7:

F0,05табл = 3,87

Fрозр > F0,05табл , робимо висновок про адекватність побудованої моделі – припускаємо присутність лінійного зв'язку.