Модели в пространстве состояний
| № | А | В | С |
| 1 |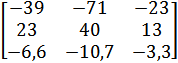 
| 
| 
|
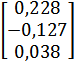
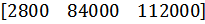
| 2 |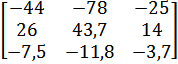 
|
|
|
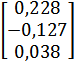
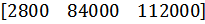
| 3 |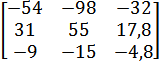 
|
| 
|
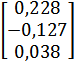
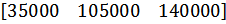
| 4 |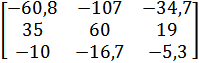 
|
|
|
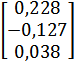
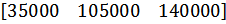
| 5 |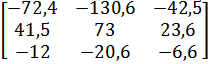 
|
| 
|
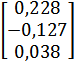
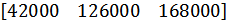
| 6 |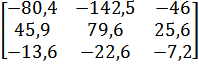 
|
|
|
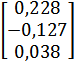
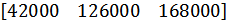
| 7 |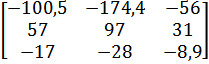 
|
|
|
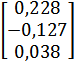
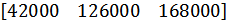
| 8 |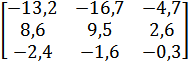 
|
| 
|
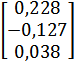
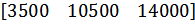
| 9 |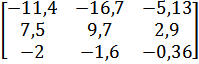 
|
| 
|
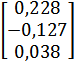
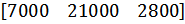
| 10 |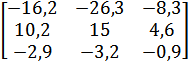 
|
| 
|
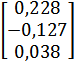
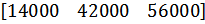
| 11 |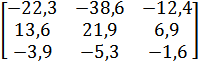 
|
| 
|
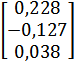
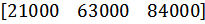
| 12 |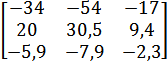 
|
|
|
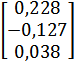
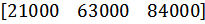
3. С помощью выбора масштабирующего коэффициента обеспечить в системе нулевую установившуюся ошибку.
4. Собрать в Simulink MatLab структурную схему системы с модальным регулятором (не используя блок State space) и проверить полученные результаты.
- Содержание отчета
Отчет о лабораторной работе должен содержать:
1. Краткие теоретические сведения
2. Расчетную часть
3. Структурные схемы моделирования в Simulink
4. Графики переходных процессов в системе.
5. Выводы о проделанной работе.
Контрольные вопросы
1. Что такое состояние, пространство состояний, вектор состояния?
2. Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.
3. Что такое «мода»?
4. Какая система является управляемой?
5. Что такое степень устойчивости?
6. Что представляет собой модальный регулятор?
7. Поясните суть модального управления.
ЛАБОРАТОРНАЯ РАБОТА № 9
НАБЛЮДАЮЩИЕ УСТРОЙСТВА
Цель лабораторной работы – изучение возможности модального управления с помощью критерия управляемости.
Продолжительность лабораторной работы – 4 часа
- Краткие теоретические сведения
Метод модального управления предполагает, что все компоненты вектора состояния X могут быть измерены. Однако на практике некоторые компоненты могут быть неизвестны по одной из двух причин:
– измерительных приборов может быть недостаточно;
– некоторые компоненты вектора X могут не иметь физического смысла.
Однако если система является наблюдаемой, то все компоненты вектора X могут быть восстановлены по наблюдениям вектора Y.
Система, описываемая матрицами А и С, является наблюдаемой тогда и только тогда, когда существует конечное время Т такое, что начальное состояние X(0) может быть определено в результате наблюдения выходной переменной y(t), при заданном управлении u(t).
Наблюдаемость системы описывается условием:
|
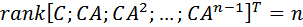
Для системы с одним входом и одним выходом матрица управляемости (размером n × n) имеет вид:
|
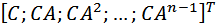
Если детерминант этой матрицы отличен от нуля, то система наблюдаема.
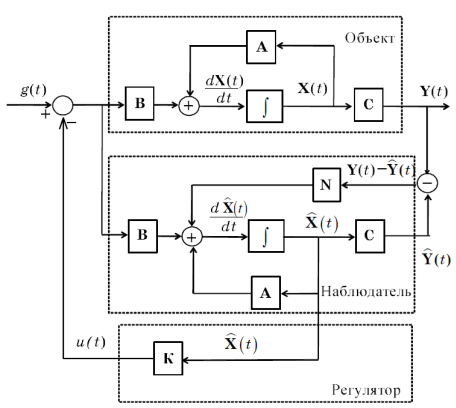
Для того чтобы узнать все компоненты вектора состояния объекта, можно использовать его модель
|
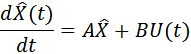
где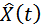 
– оценка состояния объекта.
Если начальное состояние объекта и модели совпадают и модель адекватна объекту, то можно полагать в любой момент времени, что
 .
|
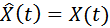Однако практически добиться полной адекватности объекта и модели невозможно, невозможно может быть и полное равенство начальных условий. Поэтому на практике можно рассчитывать лишь на выполнение условия
 .
|
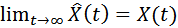Подобным свойством обладают так называемые асимптотические наблюдающие устройства.
Асимптотическое наблюдающее устройство использует обратную связь по ошибке восстановления вектора состояния, так что работа наблюдающего устройства описывается уравнением
|
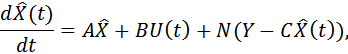
где N – матрица параметров наблюдающего устройства.
Общий вид системы управления с наблюдателем показан на рис. 9.1. Модель наблюдателя показана на рис. 9.2.
