Рис. 8.1. Система с обратной связью
Аккерманом была предложена формула, позволяющая с помощью преобразования подобия перевести модель произвольной структуры в каноническую форму управляемости, определить искомые коэффициенты К, а затем пересчитать полученное решение применительно к исходной структуре. Формула Аккермана имеет вид [3]
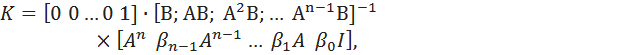
где B – коэффициенты характеристического полинома матрицы (А– ВK).
Таким образом, задача модального синтеза сводится к выбору желаемых корней характеристического полинома замкнутой системы, при которых обеспечиваются заданные параметры переходного процесса, после чего в соответствии со стандартным алгоритмом рассчитываются коэффициенты обратных связей по состоянию.
Использование MatLab
В программном комплексе MatLab для формирования модели в пространстве состояний используется функция ss,
>> w1 = ss(A, B, C, D),
где A, B, C, D – матрицы модели.
Из модели в пространстве состояний можно получить ПФ команn дой:
>> w2 = tf(w1)
И, наоборот, если уже существует модель, заданная ПФ, то ее можn но преобразовать в пространство состояний с помощью команды ss:
>> w=tf([2 2],[3 4 1]);
>> w1=ss(w)
Заметим, что одной и той же ПФ могут, вообще говоря, соответn ствовать разные модели в пространстве состояний, но всем этим моделям соответствует одна и та же ПФ.
Матрица управляемости может быть построена с помощью функn ции ctrb, которая вызывается одной из команд:
>> W = ctrb(A, B)
>> W = ctrb(sys)
>> W = ctrb(sys.A, sys.B)
В пакете MatLab имеется функция acker, с помощью которой можно обеспечить желаемое расположение полюсов одномерной линейной системы (в соответствии с формулой Аккермана):
>> k = acker(A,B,P),
где А и В – матрицы системы; Р – вектор, задающий желаемое распоn ложение полюсов системы.
Пример. Пусть система описывается матрицами
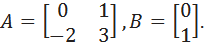
Желаемые полюса заданы вектором:
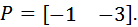
Тогда рассчитать значение коэффициентов обратных связей можно с помощью команд
>>A=[0 1;,2 3];
>> B=[0; 1];
>> P=[,1 ,3];
>> K=acker(A,B,P)
K = 1 7
Таким образом, управление в этом примере должно быть сформировано в виде
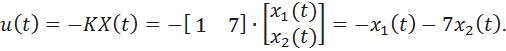
Для многомерных систем в пакете MatLab имеется функция place (ее можно использовать также и для одномерных систем). Функция
>> K=place(A,B,P)
рассчитывает матрицу коэффициентов обратных связей K, которая обеспечивает желаемое расположение полюсов системы. Длина вектора P должна быть равна числу строк матрицы А.
Следует заметить, что метод модального управления не гарантирует равенство установившейся ошибки нулю. Для обеспечения равенства задающего воздействия и выходного сигнала системы в установившемся режиме вводится масштабирующий коэффициент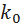 
. Для его вычисления запишем уравнения состояния в виде:
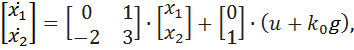
подставляя уравнение (6), имеем:
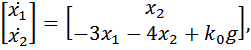
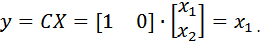
В установившемся режиме получаем
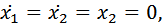
и должно выполняться условие
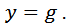
Следовательно, из уравнения (7) получаем
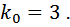
На этот коэффициент должно умножаться входное воздействие.
В пакете моделирования Simulink MatLab для описания объекта в пространстве состояний имеется блок State Space. Однако этот блок не позволяет непосредственно оценивать текущее значение вектора состояния, поэтому для моделирования работы модального регулятор нужно детально описывать матричные операции.
- Порядок выполнения работы
1. Для полученного варианта объекта управления, заданного матрицами А, В, С (см. табл.), обосновать возможность модального управления с помощью критерия управляемости.
2. Рассчитать коэффициенты обратной связи, при которой обеспечивается желаемое расположение полюсов замкнутой системы. Рассмотреть два варианта - когда перерегулирование равно 30 и 0% (апериодический процесс).
Таблица