Рис. 5.1. Модель автоматической системы для построения переходных процессов и фазовых траекторий
6. Рассчитать шаг и время переходного процесса для колебательной системы, исходя из периода собственных колебаний (шаг меньше периода в 20-50 раз) и величины демпфирования (время моделирования ориентировочно в пять раз больше этой величины). Если вещественная часть корней характеристического уравнения положительная, то ограничиться при моделировании пятью периодами.
7. Рассчитать длительность переходного процесса для апериодической системы, ограничившись пятью большими постоянными времени, при этом шаг интегрирования должен быть в 10-20 раз меньше малой постоянной.
8. Задать в окне команд MatLab значения коэффициента усиления K и постоянной времени T.
9. Задать начальное отклонение от точки равновесия в интегрирующем звене.
10. Задать параметры вывода фазовой траектории в блоке XY_Graf, равными по оси X начальному отклонению, а по оси Y произведению этого отклонения на угловую частоту собственных колебаний.
11. Задать в установках конфигурации меню Simulation рассчитанные значения длительности процесса и максимального шага интегрирования, затем запустить процесс моделирования.
12. Построить график переходного процесса в заданной системе, задав в командном окне оператор «plot(t,x)», а затем «grid on» для включения сетки.
13. Построить фазовую траекторию системы в виде графика, задав в командном окне оператор «plot(x,y)»
14. Задать в командном окне оператор «grid on», который включит на графике сетку и оператор «hold on», который заморозит график в соответствующем окне.
15. Задать в звене интегрирования новое начальное значение и повторить процесс моделирования.
16. Добавить на график новую фазовую траекторию с помощью операторов «plot(x,y)» и «grid on».
17. Повторяя несколько раз построение фазовых траекторий получить в целом фазовый портрет заданной системы.
18. Проанализировать полученные результаты моделирования, дав заключение об устойчивости автоматической системы, виде ее фазового портрета и его особых точках.
- Пример моделирования
Рассмотрим пример моделирования прикоэффициенте усиления K=8 и постоянной времени апериодического звена T=4. Передаточная функция замкнутой системы при этом принимает следующий вид:
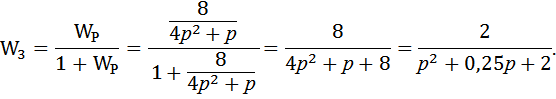
Корни характеристического уравнения
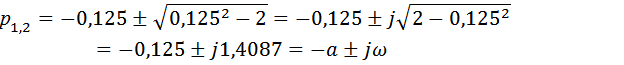
Процессы в такой системе будут носить колебательный характер с частотой f и периодом t собственных колебаний
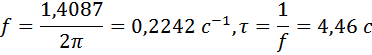
Постоянная времени, с которой уменьшается амплитуда колебаний равна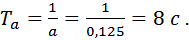 
Исходя из полученных результатов расчета, задаем время интегрирования, равное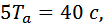 
а максимальный шаг выбираем меньше периода колебаний более чем в 40 раз и равным 0,1 с.
В блоке интегрирования задаем начальное отклонение по X, равное 10. Соответственно в блоке XY_Graf задаем отклонения по X, также равное 10, а по оси Y больше в 1,4 раза и равное 15.
Далее на рис. 5.2 показан результат моделирования в виде переходного процесса в функции времени, а на рис.3 показана фазовая траектория этого процесса. На рис.4 показан фазовый портрет системы, построенный по результатам моделирования четырех переходных процессов с соответствующими начальными отклонениями.
По результатам моделирования можно сделать выводы:
а) характер переходных процессов действительно носит колебательный характер,
б) система управления устойчива,
в) фазовый портрет состоит из траекторий в виде сужающихся эллипсов с устойчивым фокусом в точке равновесия.
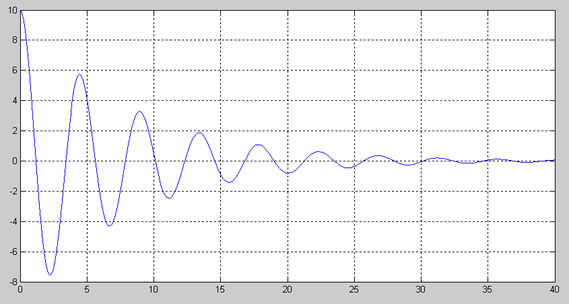
Рис. 5.2. Переходный процесс в системе при отклонении X = 10.
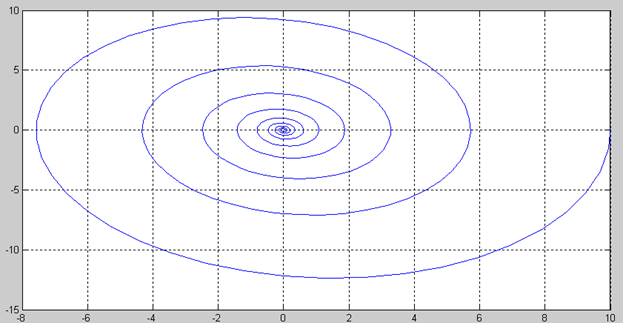
Рис. 5.3. Фазовая траектория при начальном отклонении X = 10