Использование пакета MatLab
В составе MatLab Simulink имеется пакет Nonlinear Control Design (NCD) Blockset, с помощью которого можно выполнить оптимизацию параметров ПИД-регулятора, если имеется модель объекта управления.
В наборе блоков NCD Blockset имеется основной блок NCD Outport, с помощью которого можно задать требуемые ограничения для переходного процесса в оптимизируемой системе, указать оптимизируемые параметры и выполнить параметрическую оптимизацию.
В составе NCD Blockset имеется набор демонстрационных файлов, в том числе – файл ncddemo1, показывающий процесс настройки ПИД-регулятора. После набора имени этого файла в командной строке MatLab будет открыто окно Simulink со следующей схемой (рис. 6.2).
Блок Controller представляет собой описание ПИД)регулятора, он приведен на рис. 6.3:
Блок Plant & Actuator (рис. 6.4) описывает объект управления, заданный передаточной функцией, перед которой помещены нелинейности, ограничивающие уровень входного сигнала (блок Limit) и значение его производной (блок Rate).
На выходе объекта (рис. 6.2) располагается блок оптимизации NCD_Outport, окно которого показано на рис. 6.5.
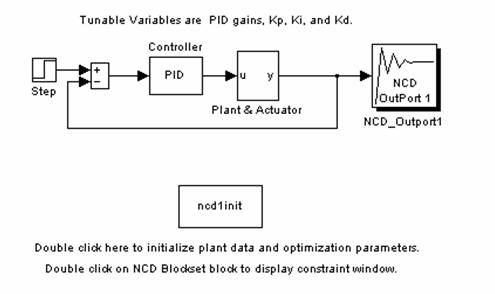
Рис. 6.2. Окно Simulink c примером ncddemo1
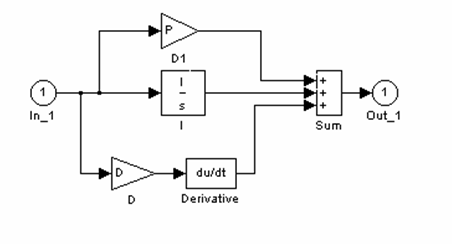
Рис. 6. 3 . ПИД-регулятор в Simulink
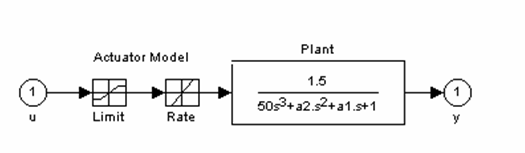
Рис. 6.4. Описание объекта управления в Simulink
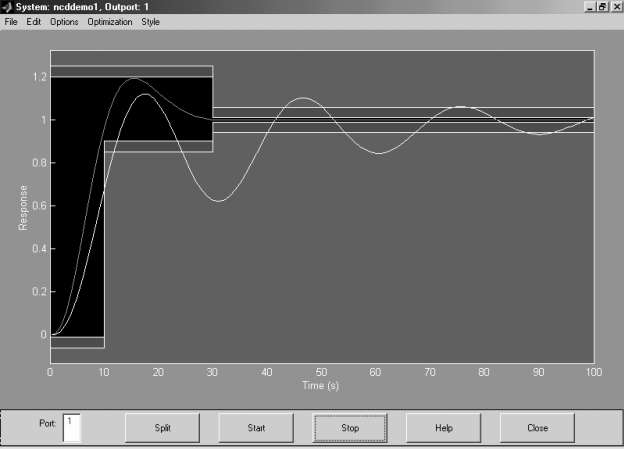
Рис. 6.5. Главное окно блока NCD_Outport
На рис. 5 показаны границы желаемого переходного процесса в системе. Пользователь может изменять их по своему усмотрению.
Кнопка Split позволяет разбивать границы на более мелкие участки для описания переходного процесса с нужной степенью подробности.
Кнопки Start и Stop управляют процессом оптимизации.
Пункты меню File и Edit содержат обычные операции работы с файлами и редактирования.
В меню Options находятся ряд опций для более детального описания и отображения переходных процессов в системе.
При выборе пункта меню Optimization/Parameters открывается
окно, в котором задаются параметры оптимизации и интервал дискретизации. Главные поля этого окна имеют следующее значение:
– Tunable variable – окно ввода имен настраиваемых параметров (в данном случае это коэффициенты ПИД)регулятора – их названия вводятся через пробел).
– Lover bound и Upper bound – нижняя и верхняя границы значений настраиваемых переменных.
– Discretization interval – интервал дискретизации.
До запуска процесса оптимизации надо задать в окне команд MatLab начальные значения коэффициентов ПИД-регулятора.
После запуска процесса оптимизации в окне NCD_Outport отображаются варианты переходного процесса при изменении настраиваемых параметров. Настройка заканчивается, когда процесс попадает в заданные границы (рис. 6.5).
В окне команд MatLab можно прочитать значения полученных параметров для рассмотренного примера:
kp = 1,33; ki = 0,15; kd = 8,33.
- Порядок выполнения работы
1. Соберите в MatLab Simulink систему управления с ПИД-регулятором для полученного варианта объекта управления (см. табл. лабораторной работы № 4).
2. Сформулировать требования к желаемому переходному процессу в системе.
3. Определить значения коэффициентов ПИД-регулятора путем интерактивного моделирования на основании методики Зиглера – Николса.
4. С помощью пакета NCD Blockset выполнить оптимизацию параметров ПИД-регулятора.
5. Рассмотрите варианты П-, И-, ПД- и ПИ-регуляторов для заданного объекта. Оптимизируйте их параметры и сравните результаты.
- Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Краткие теоретические сведения.
2. Структурные схемы исследованных регуляторов.
3. Графики переходных процессов при управлении объектом с помощью различных регуляторов.
4. Выводы о проделанной работе.
Контрольные вопросы
1. Что называется регулятором?
2. Какие типовые регуляторы вы можете назвать?
3. Запишите выражение ПИД-регулятора и охарактеризуйте его составляющие?
4. Какого типа коррекция САУ изображена на рис. 6.1?
ЛАБОРАТОРНАЯ РАБОТА № 7
ИССЛЕДОВАНИЕ ФАЗОВЫХ ПОРТРЕТОВ
ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Цель лабораторной работы - изучение возможностей исследования систем автоматического управления на основе фазового портрета этой системы, полученного моделированием на ЭВМ с помощью приложения Simulink системы компьютерной математики MatLab.
Задачей работы является приобретение навыков моделирования и исследования линейных систем автоматического управления с помощью Simulink системы MatLab.
Продолжительность работы – 2 часа.
Для замкнутых систем автоматического управления (2-3 варианта) с передаточными функциями разомкнутой части
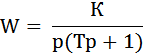
построить фазовые портреты и дать заключение о качестве регулирования. Коэффициент усиления K и время T задаются преподавателем.
- Порядок выполнения работы
1. Определить передаточную функцию замкнутой системы.
2. Найти корни характеристического уравнения замкнутой системы и дать заключение о принадлежности переходных процессов к колебательным или к экспоненциальным зависимостям.
3. Если процессы колебательные, определить для них частоту собственных колебаний и величину демпфирования.
4. Если процессы апериодические определить для них постоянные времени.
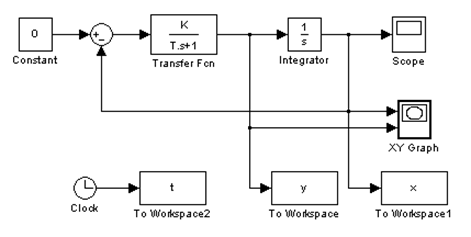
5. Запустить программу компьютерной математики MatLab и встроенный в нее модуль Simulink, задать новую модель и набрать в появившемся окне структурную схему для построения переходных процессов и фазовых траекторий по рис. 5.1.