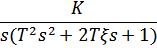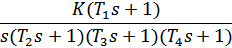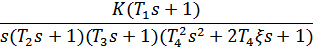Рис. 3.8. Увеличение колебательности выходного сигнала с ростом Ки
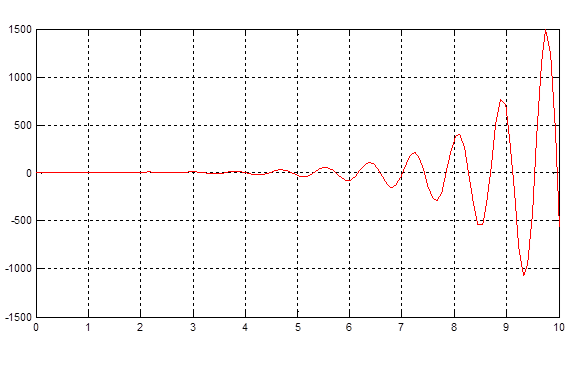
Рис. 3.9. Выходной сигнал САУ при Ки=25
Для исследования работы САУ с ПИ-регулятором необходимо иметь ненулевое значение в блоке Gain и в значении числителя интегратора. Аналогичным образом для начала примем эти значения равные по 1.
Смоделируем САУ с ПИ-регулятором и пронаблюдаем величину статической ошибки.
В случае набора параметров САУ, представленных на рис. 3.10, получим переходную характеристику и ошибку регулирования 3.11. Из результатов видно, что наличие пропорционально-интегрального регулятора также позволяет избавиться от статической ошибки и получить на выходе системы заданную величину. Однако процесс установления в заданное значение оказывается более затянут, чем для случае с И-регулятором.
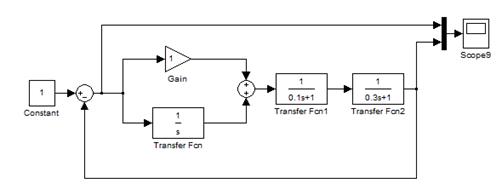
Рис. 3.10.
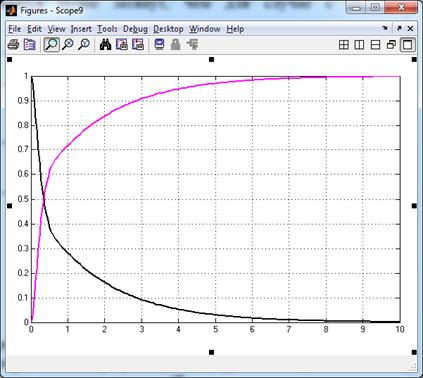
Рис. 3.11. Результаты моделирования
Анализ работы САУ с учетом значений коэффициента передачи пропорциональной части регулятора равного 1,2,5,10, 25, 50 представлены на рис. 3.12. Можно увидеть, что с ростом коэффициента К происходит изменение колебательности выходного сигнала, изменяется скорость установления в заданное значение, а также увеличивается динамическая ошибка (рис.3.13, 3.14).
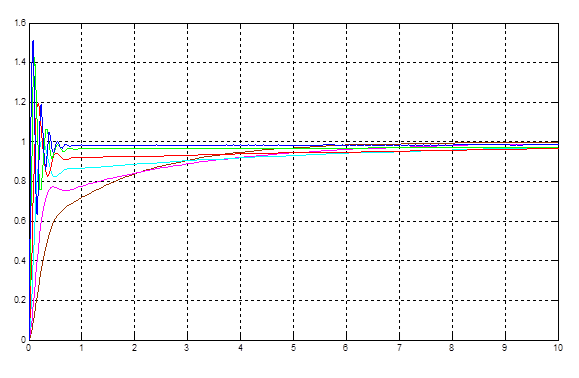
Рис. 3.12. Изменение выходного сигнала с ростом К
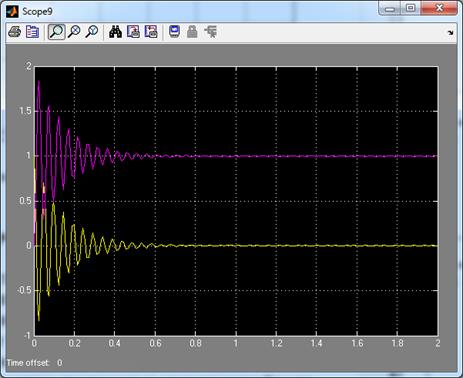
Рис. 3.13. Выходной сигнал и ошибка при К=500
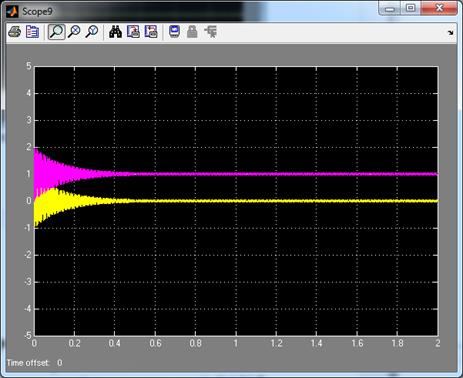
Рис. 3.14. Выходной сигнал и ошибка при К=50000
Контрольные вопросы
1. Дайте определение статической и астатической САУ.
2. Каким образом тип регулятора (П, И или ПИ) и его параметры влияют на величину статизма?
3. Каким образом тип регулятора (П, И или ПИ) влияет на характер переходного процесса?
4. Назовите виды переходных процессов и охарактеризуйте их по показателям качества.
5. Чем объясняется наличие экстремума интегральной оценки?
6. Сформулируйте критерий Гурвица для определения устойчивости замкнутой САУ.
ЛАБОРАТОРНАЯ РАБОТА № 4
МЕТОД КОРНЕВОГО ГОДОГРАФА
Цель лабораторной работы – научиться строить корневые годографы системы автоматического управления и на основе них анализировать динамику системы.
Продолжительность лабораторной работы – 4 часа.
- Краткие теоретические сведения
Корневым годографом (КГ) называется совокупность траекторий перемещения всех корней характеристического уравнения замкну) той системы при изменении какого)либо параметра этой системы.
Обычно метод КГ позволяет находить полюса и нули ПФ замкну) той системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы K.
ПФ разомкнутой системы Wp(s) представим в следующем виде:
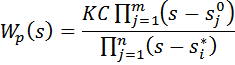
| (1) |
где 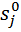 – нули ПФ
– нули ПФ 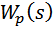 ,
, 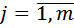 ;
; 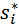 - полюса ПФ
- полюса ПФ 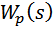 ,
, 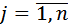 ; n и m – порядки знаменателя и числителя; C – коэффициент представле) ния (отношение коэффициентов при старших членах числителя и
; n и m – порядки знаменателя и числителя; C – коэффициент представле) ния (отношение коэффициентов при старших членах числителя и
знаменателя).
При замыкании системы с ПФ Wp(s) единичной отрицательной обратной связью ПФ замкнутой системы Wз(s) принимает вид
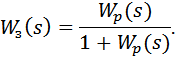
| (2) |
Из выражения (2) следует, что нули ПФ замкнутой системы равны нулям ПФ разомкнутой системы.
Для нахождения полюсов рассмотрим выражение
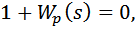
| (3) |
в соответствии с выражением (1) имеем
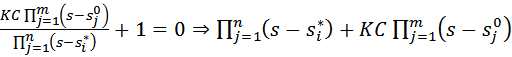
| (4) |
На основании выражения (4) можно сказать, что при K = 0 корни характеристического уравнения совпадают с полюсами, а при K = ∞ – с нулями. При изменении K от 0 до ∞ траектории корней начинаются в полюсах и заканчиваются в нулях. Обычно полюсов больше, чем нулей. В этом случае n–m ветвей корневого годографа стремятся к ∞.
Для определения полюсов замкнутой системы с отрицательной обратной связью необходимо решить уравнение (его называют основным уравнением метода КГ):
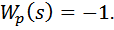
| (5) |
Так как Wp(s) является функцией комплексного переменного s, то уравнение (5) распадается на два уравнения: уравнение модулей
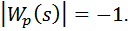
| (6) |
и уравнение аргументов (фаза вектора –1 есть нечетное число π):
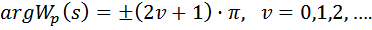
| (7) |
Как известно, при умножении комплексных чисел их аргументы складываются, а при делении – вычитаются. Поэтому, исходя из выражения (1), уравнение (7) имеет наглядный геометрический смысл.
Пусть точка s – полюс замкнутой системы. Если провести в s вектора из всех нулей Wp(s) (обозначим аргументы этих векторов 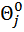 ) и вектора из всех полюсов W p(s) (обозначим аргументы этих векторов
) и вектора из всех полюсов W p(s) (обозначим аргументы этих векторов 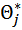 ), то уравнение (7) можно записать в следующем виде:
), то уравнение (7) можно записать в следующем виде:
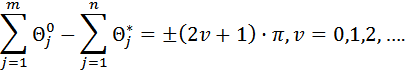
| (8) |
Углы q отсчитываются от положительного направления действительной оси. Знак угла .+. соответствует повороту против часовой стрелки, знак угла .–. соответствует повороту по часовой стрелке.
Таким образом, любая точка КГ должна удовлетворять уравне нию (8), из которого следует, что конфигурация КГ не зависит от коэффициента усиления K, но каждому конкретному значению K однозначно соответствуют точки на КГ.
При умножении комплексных чисел их модули перемножаются, а при делении – делятся. Поэтому на основании уравнения (6) можно записать
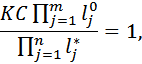
| (9) |
где 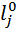 – модуль (длина) вектора, проведенного из j)нуля в точку s КГ;
– модуль (длина) вектора, проведенного из j)нуля в точку s КГ; 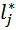 – модуль вектора, проведенного из i-полюса в ту же точку s.
– модуль вектора, проведенного из i-полюса в ту же точку s.
Таким образом, траектории корней строятся только по уравнениям фаз, а уравнение модулей используется затем для нахождения К.
Сущность метода КГ заключается в том, чтобы узнать, каким должен быть коэффициент усиления разомкнутой системы, чтобы было обеспечено желаемое положение корней замкнутой системы.
Корневой годограф системы с отрицательной обратной связью обладает следующими основными свойствами [1–4]:
1. Ветви КГ непрерывны и расположены на комплексной плоскости симметрично относительно действительной оси.
2. Число ветвей КГ равно порядку системы n. Ветви начинаются в n полюсах разомкнутой системы при K = 0. При возрастании K от 0 до ∞ полюса замкнутой системы двигаются по ветвям КГ.
3. m ветвей КГ при возрастании K от 0 до ∞ заканчиваются в m нулях Wp(s), a (n – m) ветвей при K, стремящемся к ∞, удаляются от полюсов вдоль асимптот.
4. При расположении ветвей корневого годографа в левой полуплоскости s САУ устойчива. При пересечении ветвей КГ мнимой оси слева направо САУ становится неустойчивой. Пусть при K = Kкр пересечение КГ с мнимой осью произойдет в некоторой точке iωкр. Назовем это значение коэффициента усиления критическим Kкр, а величину ωкр критической угловой частотой, на которой система становится неустойчивой.
Использование пакета MatLab
В системе MatLab существует команда zpk для преобразования модели, заданной ПФ, в модель, заданную нулями, полюсами и обобщенным коэффициентом передачи (zpk форма).
Пример :
>> w=tf([10],[2 2 3 1 0])
Transfer function:
10
——————————
2 s^4 + 2 s^3 + 3 s^2 + s
>> w1=zpk(w)
Zero/pole/gain:
5
———————————————
s (s+0.3966) (s^2 + 0.6034s + 1.261)
Для работы с корневым годографом удобно использовать графический интерфейс «SISO-Design Tool», предназначенный для анализа и синтеза одномерных линейных систем автоматического управления (SISO – Single Input/Single Output).
Запуск SISO-Design Tool осуществляется командой
>> sisotool
Графический интерфейс «SISO-Design Tool» представлен на рис. 4.1
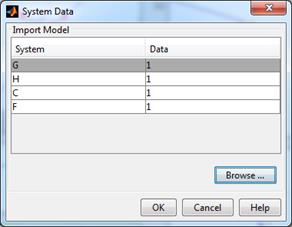
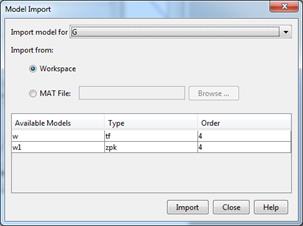
В появившемся окне графического интерфейса необходимо использовать команду «File/Import» для загрузки данных из рабочего пространства MatLab, в результате которой появляется диалоговое окно Import System Data (рис. 4.2).
После импортирования данных можно исследовать изменение временных и частотных характеристик замкнутой системы при изменении К. Обычно при этом требуется определить условия неустойчивости замкнутой САУ. Определить Kкр и ωкр.
На рис. 4.3 показано окно sisotool для описанной выше модели w1. Двигая красным курсором по КГ до пересечения ветвей с мнимой осью, можно определить значение Kкр. В данном случае Kкр ≈ 0,1. Значение ωкр соответствует мнимой координате пересечения КГ мнимой оси. Просмотреть это значение можно в нижней части интерфейса или выбрав меню «View/Closed-Loop Poles».
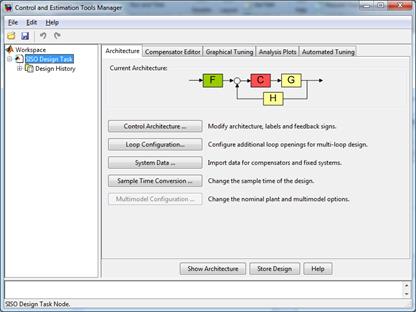
(а)
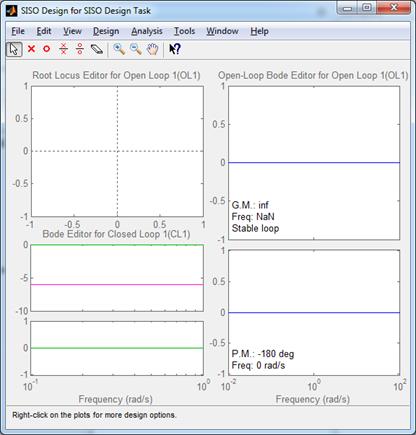
(б)
Рис. 4.1. Графический интерфейс «SISO-Design Tool»: (а) – окно, в котором предлагается структура САУ; (б) – окно результатов
| 
|
Рис. 4.2. Диалог для ввода параметров модели
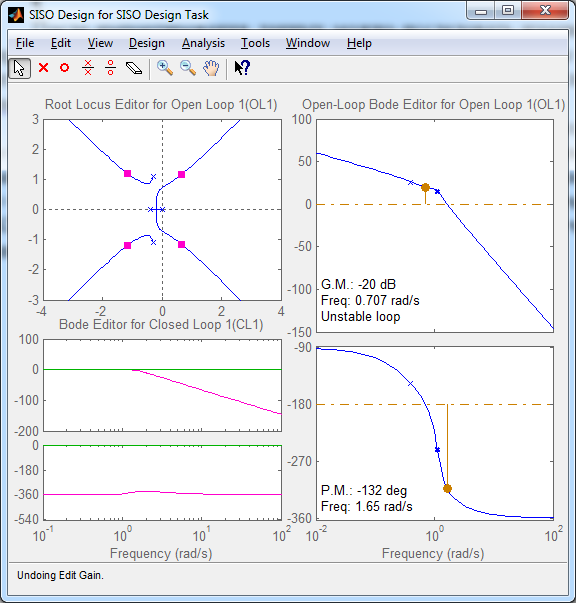
Рис. 4.3. Основное окно SISO Design tool с результатами.
- Порядок выполнения работы
1. Рассчитайте нули и полюса передаточной функции согласно варианту из таблицы.
Таблица 4.1
Варианты передаточных функций
| № по п/п | Значения параметров | Передаточная функция разомкнутой системы |
| 1. | T = 0,1, ξ= 1 |
|
| 2. | T = 0,05, ξ= 0,707 | |
| 3. | T = 0,03, ξ= 0,1 | |
| 4. | T = 0,08, ξ= 0,5 | |
| 5. | T = 0,01, ξ= 0,15 | |
| 6. | T1 = 0,03, T2 = 0,5, T3 = 0,1, T4 = 0,05 |
|
| 7. | T1 = 0,05, T2 = 0,4, T3 = 0,08, T4 = 0,033 | |
| 8. | T1 = 0,2, T2 = 0,45, T3 = 0,1, T4 = 0,05 | |
| 9. | T1 = 0,5, T2 = 0,25, T3 = 0,1, T4 = 0,02 | |
| 10. | T1 = 0,1, T2 = 0,25, T3 = 0,1, T4 = 0,05 | |
| 11. | T1 = 0,2, T2 = 0,1, T3 = 0,05, T4 = 0,07, ξ = 0,5 |
|
| 12. | T1 = 0,07, T2 = 0,1, T3 = 0,05, T4 = 0,07, ξ = 0,5 | |
| 13. | T1 = 0,3, T2 = 0,1, T3 = 0,05, T4 = 0,07, ξ = 0,5 | |
| 14. | T1 = 0,01, T2 = 0,1, T3 = 0,1, T4 = 0,07, ξ = 0,5 | |
| 15. | T1 = 0, T2 = 0,1, T3 = 0,1, T4 = 0,07, ξ = 0,5 |
2. Постройте нули и полюса на комплексной плоскости.
3. Постройте КГ в соответствии с вариантом из п.1. при помощи графического интерфейса sisotool.
4. Сравните результаты расчетов п. 1 и п. 3.
5. Исследуйте динамику замкнутой системы при различных значениях коэффициента усиления разомкнутой системы K, в том числе:
– запасы устойчивости в частотной области;
– параметры переходного процесса во временной области.
- Содержание отчета
Отчет о лабораторной работе должен содержать:
1. Краткие теоретические сведения.
2. Результаты расчетов и графические построения по п. 1-3
3. Анализ результатов построения КГ.
4. Анализ результатов исследования динамики системы.
5. Выводы об адекватности полученных результатов.
Контрольные вопросы
1. Что такое корневой годограф?
2. Что такое нули и полюса передаточной функции?
3. Какое уравнение называется основыным уравнением метода корневого годографа?
4. Назовите суть метода корневого годографа.
5. Назовите основные свойства корневого годографа системы с отрицательной обратной связью
ЛАБОРАТОРНАЯ РАБОТА № 5
ИССЛЕДОВАНИЕ ЗАМКНУТЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С
ЖЕСТКОЙ ОБРАТНОЙ СВЯЗЬЮ
Цель лабораторной работы - приобретение навыков синтеза последовательных корректирующих звеньев, определение показателей качества замкнутых систем автоматического управления (САУ) по переходным и частотным характеристикам.
Продолжительность лабораторной работы – 4 часа.
- Порядок выполнения работы
1. Разработать модель объекта регулирования в MatLab Simulink (рис. 4.1, табл. 4.1) во временной и частотной областях. Получить на модели частотные и переходные характеристики системы, определить показатели качества системы
2. Рассчитать передаточную функцию объекта регулирования по задающему воздействию.
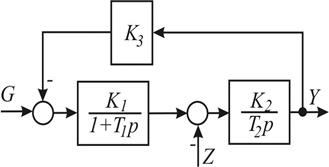
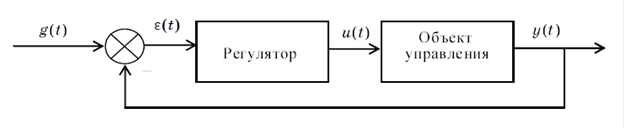
Рис. 4.1. Структурная схема объекта регулирования
Таблица 1
| № вар. | 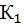
| 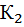
| 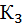
| 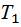 , с , с
| 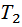 , с , с
| G | Z |
| 1 | 10 | 0,02 | 5 | 0,01 | 0,095 | 1…5 | 0…6 |
| 2 | 2,86 | 0,28 | 1,25 | 0,14 | 0,98 | 2…12 | 3…8 |
| 3 | 8,5 | 0,15 | 0,8 | 0,012 | 0,063 | 5…9 | 2…6 |
| 4 | 3,33 | 0,5 | 0,6 | 0,02 | 0,12 | 4…8 | 3…7 |
| 5 | 6,6 | 0,22 | 0,69 | 0,08 | 0,55 | 2…10 | 0…5 |
| 6 | 10 | 0,09 | 1,11 | 0,12 | 0,6 | 3…6 | 3…6 |
| 7 | 10 | 0,1 | 1 | 0,1 | 0,43 | 4…12 | 0…7 |
| 8 | 6 | 0,39 | 0,43 | 0,59 | 2,95 | 5…15 | 3…9 |
| 9 | 17 | 0,15 | 0,39 | 1,5 | 7,1 | 2…6 | 5…12 |
| 10 | 3,75 | 0,64 | 0,42 | 0,07 | 0,39 | 10…20 | 4…12 |
| 11 | 8,3 | 0,95 | 0,13 | 0,2 | 0,96 | 5…11 | 3…10 |
| 12 | 6 | 0,17 | 0,98 | 0,067 | 3,55 | 3…8 | 5…11 |
| 13 | 19 | 0,7 | 0,075 | 0,42 | 1,92 | 2…10 | 10…18 |
| 14 | 4 | 0,75 | 0,333 | 0,17 | 0,99 | 3…11 | 3…11 |
3. Рассчитать параметры последовательного корректирующего звена, производящего настройку системы, замкнутой жесткой отрицательной единичной обратной связью, на технический оптимум.
4. Разработать модель системы в MatLab Simulink по п. 3 во временной и частотной областях. Получить на модели частотные характеристики разомкнутой системы и переходные характеристики замкнутой системы, определить показатели качества системы, сравнить их с теоретическими характеристиками.
5. Рассчитать параметры последовательного корректирующего звена, производящего настройку системы, замкнутой жесткой отрицательной единичной обратной связью, на симметричный оптимум.
6. Разработать модель системы в MatLab Simulink по п. 5 во временной и частотной областях. Получить на модели частотные характеристики разомкнутой системы и переходные характеристики замкнутой системы, определить показатели качества системы, сравнить их с теоретическими характеристиками.
- Содержание отчета
Отчет о лабораторной работе должен содержать:
1. Расчет передаточной функции объекта регулирования по задающему воздействию.
2. Расчет последовательного корректирующего звена по п. 2 и 4 задания.
3. Модель в MatLabSimulink и графики переходных и частотных характеристик по п. 1, 4 и 6 задания.
Графики переходных процессов должны отображать:
- переходные процессы при скачкообразном изменении задающего сигнала при граничных значениях возмущающего сигнала. Величина скачка соответствует максимальному и минимальному значениям задающего сигнала;
- переходные процессы при скачкообразном изменении возмущающего сигнала при граничных значениях выходного сигнала. Величина скачка соответствует максимальному и минимальному значениям возмущающего сигнала.
4. Определение типовых показателей качества переходных процессов по п. 4 и 6 задания.
5. Выводы об адекватности полученных результатов.
Контрольные вопросы
1. Дайте определение типовым показателям качества регулирования в системах автоматического регулирования.
2. Перечислите типовые соединения динамических звеньев. Приведите примеры их преобразования.
3. В чем назначение последовательных корректирующих звеньев?
4. Как определяют параметры последовательных корректирующих звеньев?
5. Каковы параметры системы при настройке на технический оптимум и симметричный оптимумы? Как выглядят переходные и частотные характеристики системы, каковы при этом показатели качества регулирования?
ЛАБОРАТОРНАЯ РАБОТА № 6
ИССЛЕДОВАНИЕ ПИД РЕГУЛЯТОРОВ
Цель лабораторной работы – изучение работы ПИД регулятора.
Продолжительность работы – 4 часа.
- Краткие теоретические сведения
Классическая схема управления с единичной отрицательной обратной связью показана на рис. 6.1.