Рис. 2.1. Исходная структура САУ
Преобразование включает несколько этапов, показанных на рис.2.2-2.5.
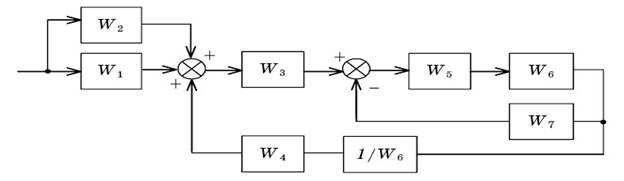
Рис. 2.2. Перенос узла через сумматор
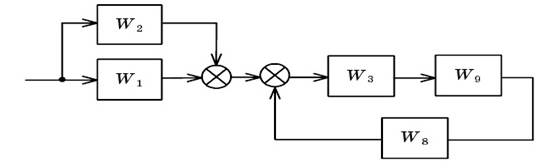
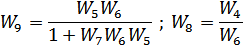
Рис. 2.3. Свертывание обратной связи и последовательного соединения
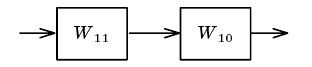
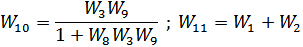
Рис. 2.4. Свертывание обратной связи и параллельного соединения
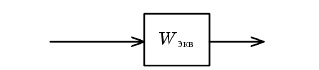
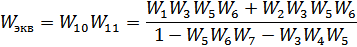
Рис. 2.5. Свертывание последовательного соединения
Таким образом, первый способ преобразования структурных схем заключается в непосредственном использовании правил, приведенных в табл.2.1. Неудобство использования этого подхода заключается в том, что порядок применения формул здесь достаточно произволен, возможны ошибочные шаги, усложняющие поиск решения.
Второй способ для получения ПФ многоконтурной системы заключается в использовании модели системы в виде сигнального графа.
Сигнальный граф позволяет графически описать линейные связи между переменными, он состоит из узлов (вершин) и соединяющих их направленных ветвей.
Ветвь соответствует блоку структурной схемы, она отражает зависимость между входной и выходной переменными. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную.
Последовательность ветвей между двумя узлами называется путем. Контуром называется замкнутый путь, который начинается и заканчивается в одном и том же узле, причем ни один узел не встречается на этом пути дважды. Коэффициент передачи контура - это произведение всех входящих в него дуг.
Контуры называются не касающимися, если они не имеют общих узлов.
Сигнальный граф однозначно соответствует структурной схеме.
Пусть X(s) и Y(s) - входная и выходная переменные системы. Тогда для вычисления ПФ системы управления по ее графу можно воспользоваться формулой Мейсона:
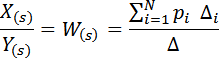
где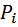 
– i-й путь от входа к выходу; N - количество путей; 
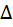- определитель графа; 
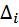- дополнительный множитель для пути.
Определитель графа получается по формуле:
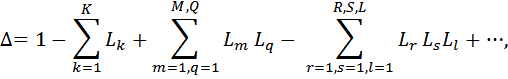
где -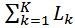 
сумма коэффициентов передачи всех отдельных контуров;
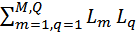- сумма произведений всех возможных комбинаций из двух не касающихся контуров;
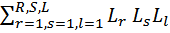- сумма произведений всех возможных комбинаций из трех не касающихся контуров.
Дополнительный множитель для i-го пути равен определителю графа, в котором приравнены нулю коэффициенты передачи контуров, касающихся этого пути.
Рассмотрим пример получения ПФ многоконтурной системы с использованием формулы Мейсона для структуры рис. 1, которой соответствует граф, показанный на рис. 2.6.
От входа к выходу ведут два пути:
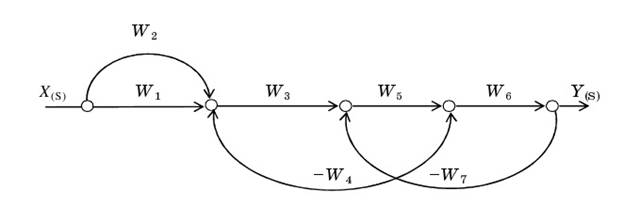
Рис. 2.6. Описание системы управления сигнальным графом
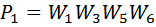
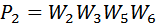
В графе есть два контура:
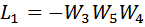
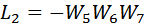
Контур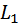 
касается контура 
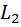, поэтому определитель графа вычисляется по формуле:
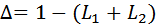
Контуры в этом примере касаются всех путей, поэтому дополнительные множители путей
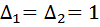
Окончательно можно записать:
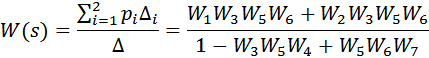
Таким образом, использование сигнальных графов и применение формулы Мейсона позволяет алгоритмизировать процесс упрощения структурной схемы.
Использование пакета MatLab
Для проверки правильности проведенных преобразований необходимо собрать схему исходной САУ и соответствующую ей эквивалентную схему в MatLab Simulink. Задача считается решенной, если при подаче на вход обоих схем одинаковых тестовых воздействий наблюдаются одинаковые выходные сигналы.
- Порядок выполнения работы
Выполните преобразование заданного варианта структурной схемы САУ в эквивалентную ПФ двумя способами:
-непосредственно используя правила табл.2.1;
-используя представление в виде сигнального графа и формулу Мейсона.
Варианты заданий приведены в табл.2.2.
В качестве звеньев W1-W3 используйте типовые динамические звенья c параметрами, выбранными в лабораторной работе №1.
- Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Описание всех этапов преобразования исходной схемы и получающихся промежуточных результатов, включающее моделирование реакции схемы на типовое воздействие (скачок) до и после преобразования;
2. Сигнальный граф системы, описание путей, контуров и расчет ПФ по формуле Мейсона;
3. Схемы экспериментов в Simulink MatLab и протокол команд MatLab.
4. Графики переходных процессов при подаче на вход исходной и эквивалентной схемы типовых тестирующих воздействий воздействий (импульс, скачок, синусоида).
5. Выводы о проделанной работе.
Таблица 2.2
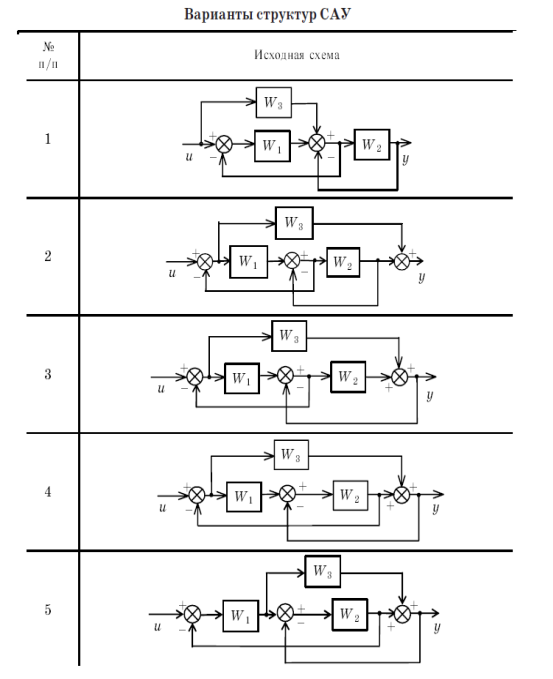
Методический пример в Matlab
В качестве примера возьмем схему рис. 2.1 со следующими передаточными функциями блоков (рис. 2.7).
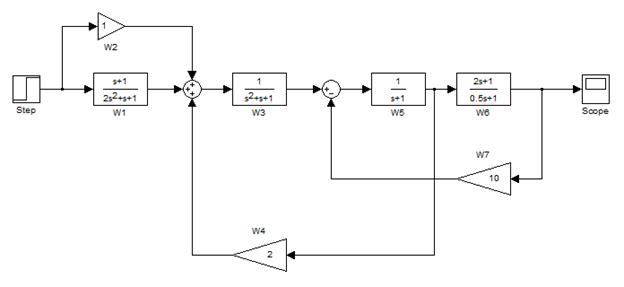
Рис. 2.7. Модель САУ
Согласно алгоритму преобразования, представленному выше получим рис. 2.8.
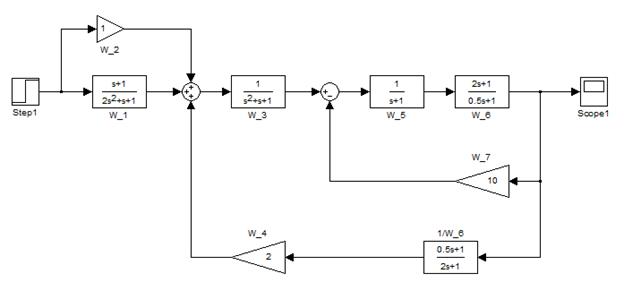
Рис. 2.8. Преобразованная модель САУ
В пакете MatLab имеется ряд функций, с помощью которых можно выполнять структурные преобразования:
- series(w1,w2) - последовательное соединение динамических звеньев;
- parallel(w1,w2) - параллельное соединение динамических звеньев;
-feedback(w1,w2) - включение звена w2 в контур отрицательной обратной связи к w1;
- feedback(w1,w2,sign) - включение звена w2 в контур обратной связи звена w1 с указанием знака + или - (очевидно, feedback(w1,w2)=feedback(w*,w2, -1));
Преобразуем САУ с использованием вышепредставленных команд. Преобразование контура, содержащего элементы c передаточными функциями W5, W6 и W7 представлены ниже.
>> w5=tf([1],[1 1])
Transfer function:
1
-----
s + 1
>> w6=tf([2 1],[0.5 1])
Transfer function:
2 s + 1
---------
0.5 s + 1
>> w56=series(w5,w6)
Transfer function:
2 s + 1
-------------------
0.5 s^2 + 1.5 s + 1
>> w7=tf([10])
Transfer function:
10
>> w567=feedback(w56,w7)
Transfer function:
2 s + 1
---------------------
0.5 s^2 + 21.5 s + 11
В результате схема САУ с преобразованным контуром W5, W6 и W7 имеет вид, представленный на рис. 2.9. Аналогичным образом преобразуются и все остальные контуры САУ.
Итоговая схема САУ имеет вид представленный на рис. 2.10.
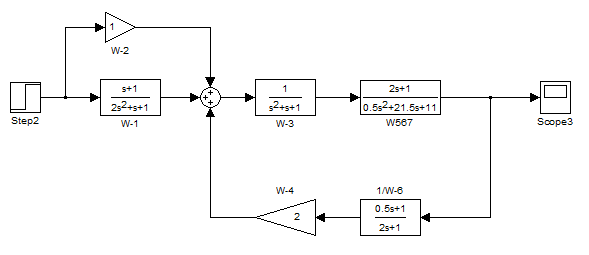
Рис. 2.9. САУ с преобразованным контуром W5, W6 и W7
Рис. 2.10. Итоговая САУ
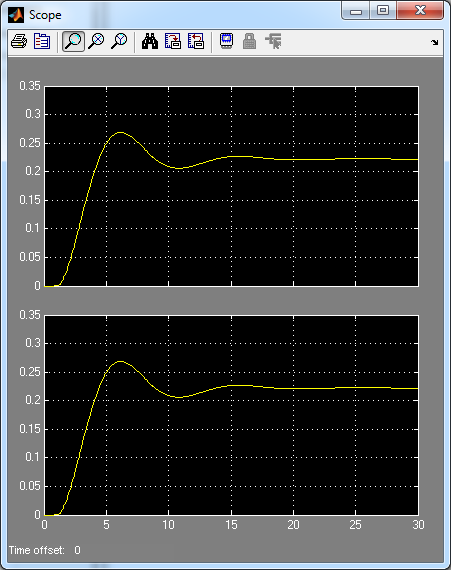
Для проверки правильности проведенных преобразований собираем схему исходной САУ (рис. 2.7) и соответствующую ей эквивалентную схему (рис. 2.10). Подаем на вход обоих схем одинаковые тестовые воздействия и наблюдаем одинаковые выходные сигналы (рис. 2.11 – 2.12).
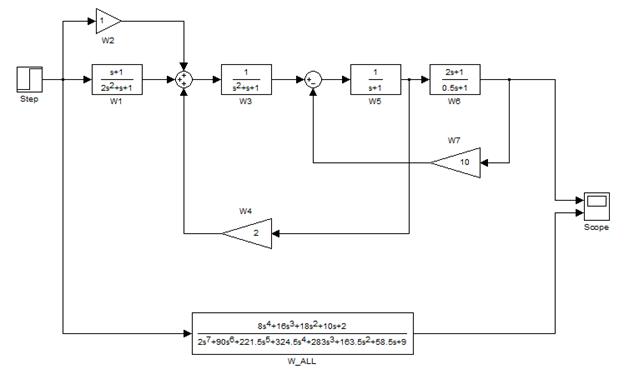
Рис. 2.11. Исходная и итоговая САУ
