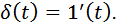Учебно-методическое пособие по использованию MATLAB / Simulink для выполнения лабораторных работ по курсу «Теория автоматического управления»
А.А. Малаханов, В.А. Хвостов
Учебно-методическое пособие по использованию MATLAB / Simulink для выполнения лабораторных работ по курсу «Теория автоматического управления»
Брянск 2015
СОДЕРЖАНИЕ
Предисловие.. 3
Краткое введение в MATLAB и Simulink.. 4
ЛАБОРАТОРНАЯ РАБОТА № 1 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.. 7
ЛАБОРАТОРНАЯ РАБОТА № 2 ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАНИЙ СТРУКТУРНЫХ СХЕМ... 13
ЛАБОРАТОРНАЯ РАБОТА № 3 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ И КАЧЕСТВА ЛИНЕЙНОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 22
ЛАБОРАТОРНАЯ РАБОТА № 4 МЕТОД КОРНЕВОГО ГОДОГРАФА 26
ЛАБОРАТОРНАЯ РАБОТА № 5 ИССЛЕДОВАНИЕ ЗАМКНУТЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ЖЕСТКОЙ ОБРАТНОЙ СВЯЗЬЮ 34
ЛАБОРАТОРНАЯ РАБОТА № 6 ИССЛЕДОВАНИЕ ПИД РЕГУЛЯТОРОВ 37
ЛАБОРАТОРНАЯ РАБОТА № 7 ИССЛЕДОВАНИЕ ФАЗОВЫХ ПОРТРЕТОВ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.. 44
ЛАБОРАТОРНАЯ РАБОТА № 8 МОДАЛЬНОЕ УПРАВЛЕНИЕ.. 50
ЛАБОРАТОРНАЯ РАБОТА № 9 НАБЛЮДАЮЩИЕ УСТРОЙСТВА.. 58
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 64
Предисловие
Пособие по лабораторному практикуму содержит 9 лабораторных работ по части линейной теории автоматического управления (ТАУ) и 8 работ по части нелинейного ТАУ. По всем лабораторным работам приведен достаточно подробный теоретический материал, методический материал по правилам работы с программным комплексом, представлены примеры реализации вариантов заданий, контрольные вопросы.
Все работы выполняются на персональном компьютере с помощью программного комплекса MATLAB/Simulink.
Пособие рекомендуется использовать для самостоятельного изучения соответствующих разделов и организации лабораторного практикума по дисциплине «Теория автоматического управления». При использовании пособия для проведения лабораторного практикума заключительным этапом работы является подготовка отчета и собеседование по представленному отчету.
Пособие предназначено для студентов направлений подготовки бакалавров 210100 (11.03.04) - «Электроника и наноэлектроника» и 140400 – «Электроэнергетика и электротехника».
Краткое введение в MATLAB и Simulink
MATLAB® - это язык программирования высокого уровня и интерактивная среда для численных экспериментов и вычислений, программирования и визуализации результатов. Используя MATLAB можно анализировать данные, разрабатывать алгоритмы, создавать модели и приложения.
Язык, инструменты и встроенные математические функции позволяют исследовать различные подходы и достичь решения быстрее, чем при использовании электронных таблиц или традиционных языков программирования высокого уровня, таких как C/C++ или Java ®. MATLAB можно использовать для целого ряда приложений, включая обработку сигналов, систем связи, обработки изображения и видео, систем управления, испытаний и измерений, финансовых вычислений и биоинформатики. Более чем миллион инженеров и ученых в промышленности и научных кругах используют MATLAB – язык технических вычислений.
MATLAB – это аббревиатура от сокращения «матричная лаборатория» (matrix laboratory). В то время как другие языки программирования главным образом работают с числами, MATLAB предназначен для работы с матрицами и массивами.
Все переменные MATLAB, многомерные массивы, независимо от того, какой тип данных. Матрица — двумерный массив, который часто используется для линейной алгебры.
За счет матричного и векторного представления данных разработчикам удалось существенно повысить скорость вычислений, экономно использовать ресурсы памяти и обеспечить высокую точность расчетов.
Система MATLAB состоит из следующих основных частей:
Язык MATLAB . Это язык матриц и массивов высокого уровня с управлением потоками, функциями, структурами данных, вводом-выводом и особенностями объектно-ориентированного программирования. Это позволяет как программировать в "малом масштабе" для быстрого создания черновых программ, так и в "большом" для создания больших и сложных приложений.
Среда MATLAB . Это набор инструментов и приспособлений, с которыми работает пользователь или программист MATLAB. Она включает в себя средства для управления переменными в рабочем пространстве MATLAB, вводом и выводом данных, а также создания, контроля и отладки М-файлов и приложений MATLAB.
Управляемая графика. Это графическая система MATLAB, которая включает в себя команды высокого уровня для визуализации двух- и трехмерных данных, обработки изображений, анимации и иллюстрированной графики. Она также включает в себя команды низкого уровня, позволяющие полностью редактировать внешний вид графики, также как при создании Графического Пользовательского Интерфейса (GU1) для MATLAB приложений.
Библиотека математических функций. Это обширная коллекция вычислительных алгоритмов от элементарных функций, таких как сумма, синус, косинус, комплексная арифметика, до более сложных, таких как обращение матриц, нахождение собственных значений, функции Бесселя, быстрое преобразование Фурье.
Программный интерфейс. Это библиотека, которая позволяет писать программы на Си и Фортране, которые взаимодействуют с MATLAB. Она включает средства для вызова программ из MATLAB (динамическая связь), вызывая MATLAB как вычислительный инструмент и для чтения-записи МАТ-файлов.
В MATLAB реализован модульный принцип построения с широкими возможностями модификации и расширения, что подтверждает состав этого продукта, а именно: несколько десятков пакетов прикладных программ и более двух сотен приложений и расширений, богатейшая библиотека функций, а также огромный объем документации, насчитывающий десятки тысяч страниц.
Для удобства пользования вся система MATLAB поделена на разделы, оформленные в виде пакетов программ, наиболее общие из которых образовали ядро.
Другие пакеты объединены или существуют индивидуально в виде так называемых Toolboxes.
Особо следует выделить пакет Simulink, предназначенный для моделирования динамических систем. Он представляет собой среду, управляемую мышью, которая позволяет моделировать процесс пугем перетаскивания блоков диаграмм на экране и их манипуляцией. Simulink работает с линейными, нелинейными, непрерывными, дискретными, многомерными системами. При этом математическая модель, описывающая поведение таких систем, формируется и решается автоматически.
Для исследователя Simulink создает массу возможностей, начиная от функционального представления устройства и вплоть до генерирования кодов, используемых для программирования микропроцессоров.
Описание работы с матрицами и массивами в командном и текстовом (программном) режимах Matlab, а также основы работы в Simulink достаточно хорошо и подробно представлены как в техническом описании к программному комплексу, так и в большом количестве литературы [11111111111111] и в данном пособии не рассматриваются.
В данном пособии представлены лишь конкретные примеры по реализации задач, изучаемых в курсе «Теория автоматического управления».
ЛАБОРАТОРНАЯ РАБОТА № 1
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ЗВЕНЬЕВ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель лабораторной работы – аналитическое и имитационное исследование динамических характеристик моделей линейных звеньев систем автоматического управления (САУ) и определение их параметров по переходным и частотным характеристикам.
Продолжительность лабораторной работы – 4 часа.
- Краткие теоретические сведения
Рассмотрим систему автоматического управления (САУ), описываемую линейным дифференциальным уравнением вида:
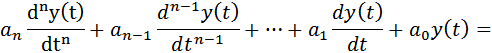
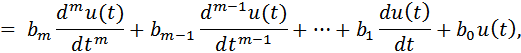
где u(t) – входной процесс; y(t) – выходной процесс;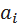 
, 
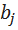, - постоянные коэффициенты; n, m (n >= m) – постоянные числа.
Если ввести обозначение p для оператора дифференцирования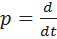 
, то можно записать (1) в операторной форме:
,
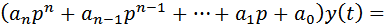
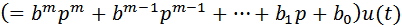откуда получается:
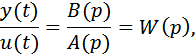
где A(p) и B(p)– полиномы из формулы (2).
Выражение (2) по виду совпадает с определением передаточной функции (ПФ), как отношения преобразования по Лапласу выходной переменной к преобразованию по Лапласу входной переменной при нулевых начальных условиях:
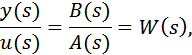
где s – комплексная переменная.
Комплексные числа, являющиеся корнями многочлена B(s), называются нулями передаточной функции, а корни многочлена A(s) -полюсами.
Описание типовых динамических звеньев приведено в таблице.
Типовые динамические звенья
| № в. | Название звена | Передаточная функция звена |
| 1 | Интегрирующее |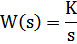 
|
| 2 | Дифференцирующее |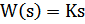 
|
| 3 | Усилительное (безынерционное) |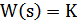 
|
| 4 | Апериодическое 1-го порядка (инерционное) |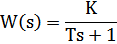 
|
| 5 | Апериодическое 2-го порядка (все корни вещественные) |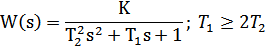 
|
| 6 | Колебательное |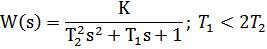 
|
| 7 | Консервативное |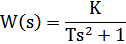 
|
| 8 | Интегрирующее с запаздыванием (реальное интегрирующее) |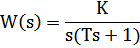 
|
| 9 | Дифференцирующее с запаздыванием (реальное дифференцирующее) |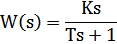 
|
| 10 | Форсирующее |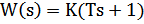 
|
| 11 | Изодромное |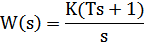 
|
Часто используется описание колебательного звена в виде:
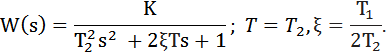
Временные характеристики динамического звена представляют собой зависимость выходного сигнала системы от времени при подаче на ее вход некоторого типового воздействия. Обычно выполняется анализ выхода системы на единичный скачок (функция Хевисайда) и импульсную функцию (функция Дирака или – дельта функция).
Единичный скачок 1(t) определяется условиями:
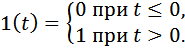
Реакция САУ на единичный скачок называется переходной функцией системы и обозначается h(t). При неединичном ступенчатом воздействии g(t)=N1(t), где N = const, в соответствии с принципом суперпозиции выходная реакция системы будет
y(t)=Nh(t) .
Импульсная функция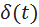 
определяется условиями:
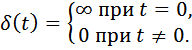
Очевидно:
