Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом.
При переходе к новой симплексной таблице будем пользоваться следующими правилами:
.
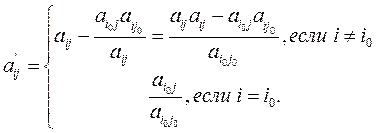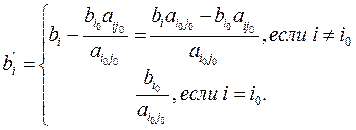
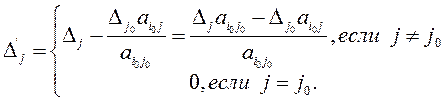
Эти же правила можно сформулировать по другому:
1. Элементы разрешающей строки новой симплексной таблицы равны элементам прежней симплексной таблицы, деленным на разрешающий элемент.
2. В разрешающем столбце все элементы, кроме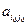 
=1, равны 0.
3. Все остальные элементы находятся по правилу прямоугольника:
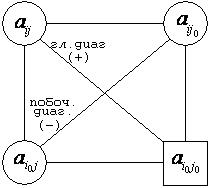
Для получения элементов новой таблицы (α ij), необходимо из произведения угловых элементов главной диагонали (содержащей искомый элемент и разрешающий элемент) вычесть произведение угловых элементов побочной диагонали и полученное число разделить на разрешающий элемент
Аналогичное правило можно сформулировать и для нахождения элементов индексной строки и столбца свободных членов.
Пусть, например, имеется симплексная таблица. Тогда правило прямоугольника выглядит следующим образом:
| БП | СБ | х1 | х2 | х3 | х4 | х5 | х6 | А0 | θ |
| 4 | 3 | 1 | 0 | 0 | 0 | ||||
| х3 | 0 | 1 | 2 | 3 | 1 | 0 | 0 | 15 | 15/1 |
| х4 | 0 | -7 | -1 | 2 | 0 | 1 | 0 | 20 | – |
| х5 | 0 | 2 | 0 | 4 | 0 | 0 | 1 | 4 | 4/2 min |
| Δj | -4 max по модулю | -3 | -1 | 0 | 0 | 0 | |||
В табличке выделены:
| – | разрешающий элемент (главная диагональ) | |
| – | искомый элемент (главная диагональ) | |
| – | элементы побочной диагонали | |
| – | выводимая из базиса переменная | |
| – | вводимая в базис переменная (заменяет выводимую из базиса переменную) |
После проведения преобразований на месте искомого элемента получим:
| БП | СБ | х1 | х2 | х3 | х4 | х5 | А0 | θ | |
| 4 | 3 | 1 | 0 | 0 | 0 | ||||
| х3 | 0 | 0 |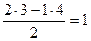 
| ||||||
| х4 | 0 | 0 | |||||||
| х1 | 4 | 1 | 0 | 2 | 0 | 0 | 0,5 | 2 | |
| Δj | 0 | ||||||||
Таким же образом производится расчет всех остальных переменных, в том числе и в индексной строке и в столбце свободных членов.
Замечания:
1. Шаг симплексных преобразований называют итерацией.
2. Если в индексной строке среди оценок свободных переменных в оптимальном плане есть равные 0, то имеет место случай альтернативного оптимума (т.е. существует по крайней мере еще хотя бы одна угловая точка ОДР являющаяся оптимальным планом => оптимальных планов бесконечно много)
3. После каждой итерации можно делать проверку правильности вычислений по следующим формулам:
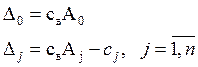
Теоремы:
1. (о существовании альтернативного оптимума)
Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая индексная оценка, соответствующая свободной переменной, то ЗЛП имеет бесконечное число оптимальных планов.
Следствие: Если в индексной строке симплексной таблицы, содержащей оптимальный план, все оценки свободны переменных положительны, то найденный оптимальный план единственный.
2. (о неограниченности целевой функции)
Если в индексной строке симплексной таблицы ЗЛП на максимум содержится отрицательная оценка или при решении задачи на минимум положительная оценка, а в соответствующем столбце нет положительных элементов, то целевая функция на множестве допустимых решений является неограниченной сверху при решении задачи на максимум или неограниченной снизу при решении задачи на минимум.