3. Переход к «нехудшему» опорному плану.
Симплекс-метод.
Этот метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов.
Симплекс-метод, впервые разработал Г.Данциг в 1947 г, данный метод известен также под названием метода последовательного улучшения плана. Его суть заключается в последовательном переборе угловых точек области допустимых решений, а алгоритмы позволяют установить, является ли данная ЗЛП разрешимой.
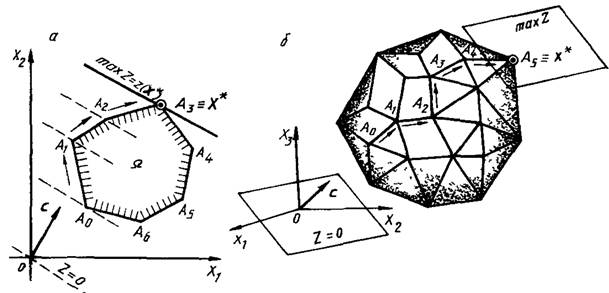
Для того чтобы построить опорный план ЗЛП при помощи симплексного метода, необходимо привести ЗЛП к предпочтительному виду (задача должна иметь канонический вид и в каждом ограничении системы должна быть переменная, входящая в него с коэффициентом 1 и с коэффициентом 0 во все остальные ограничения, именно эти переменные выбирают в качестве базиса).
Привести ЗЛП к предпочтительному виду можно следующими методами:
1. Если ЗЛП имеет канонический вид, то можно выразить первые m переменных через остальные, используя, например, метод Гаусса.
Например:
max Z = 2x1 + 3x2 – x3
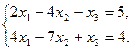
Можно свести к виду:
max Z = 2x1 + 3x2 – x3
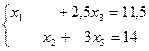
х1 и х2 – базисные переменные, х3 – свободная.
Опорный план следующий: Х* = (11,5; 14; 0)
2. Добавлением балансовых переменных (х t), удовлетворяющих описанному выше условию (+ условию неотрицательности) и входящих в целевую функцию с коэффициентом 0. Данное правило используется для задач, содержащих в системе ограничений неравенства типа «≤». При этом, вводимые в систему ограничений переменные, принимаются в качестве базисных.
Например:
max Z = x1 – x2
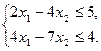
Предпочтительный вид будет следующий:
max Z = x1 – x2 + 0∙x3 + 0∙x4
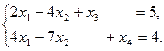
х3 и х4 – базисные переменные, х1 и х2 – свободные.
Опорный план следующий: Х* = (0; 0| 5; 4)
Вертикальная черта отделяет исходные переменные задачи от введенных.
3. Сведением к М-задаче. А именно, необходимо ввести искусственный базис (vs): переменные, удовлетворяющих описанному выше условию (+ условию неотрицательности) и входящих в целевую функцию с коэффициентом ±М, где М – очень большое число, знак «+» при решении задачи на min, знак «-» при решении задачи на max. Данное правило используется для задач, содержащих в системе ограничений неравенства типа «≥».
Например:
max Z = x1 – x2
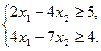
Предпочтительный вид будет следующий:
max Z = x1 – x2 – M∙v1 – M∙v2
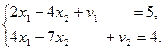
v1 и v2 – базисные переменные, х1 и х2 – свободные.
Опорный план следующий: Х* = (0; 0| 5; 4)
M-задачу по другому называют задачей с искусственным базисом.
При решении М-задачи симплекс-методом используют следующие теоремы:
1. Если в оптимальном плане Х* = (х1, х2, ..., х n| v1, v2, ..., vm) M-задачи все искусственные переменные равны 0, т.е. vS = 0, то план Х* = (х1, х2, ..., х n) является оптимальным планом исходной задачи.
2. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т.е. ее условия несовместны.
Построение оптимального плана симплекс методом происходит в 3 этапа:
1. Построение начального опорного плана;
2. Проверка плана на оптимальность;
3. Переход к «нехудшему» опорному плану.
1. Построение начального опорного плана
Пусть в ЗЛП, заданной в канонической форме, имеется n переменных и m независимых линейных ограничений.
max(min) Z=c1x1+ c2x2+…+ cnxn
X= (x1, x2, … xn) (1)
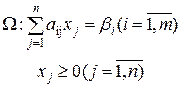
Известно, что оптимальное решение (если оно существует) достигается в одной из опорных точек (вершин ОДР), где по крайней мере k = n – m из переменных не равны 0. Выберем некоторые k переменных в качестве свободных и выразим остальные m базисных переменных.
Пусть базисными являются x1, x2, …, xm. Тогда свободными являются xm+1, xm+2, …, xn. Выразим базисные переменные, через свободные:
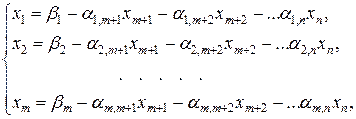 (2)
(2)
Если положить все свободные переменные xm+1, xm+2, …, xn равными 0, получим:
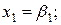
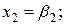 … ;
… ; 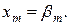
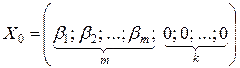
Это решение может быть допустимым или недопустимым. Оно будет допустимым, если все свободные члены 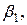
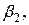 …
… 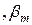 неотрицательны. Предположим, что это условие выполнено, тогда полученное решение является опорным планом. Т.о. опорным планом называется любое допустимое решение ЗЛП.
неотрицательны. Предположим, что это условие выполнено, тогда полученное решение является опорным планом. Т.о. опорным планом называется любое допустимое решение ЗЛП.
2. Проверка плана на оптимальность
Выполним некоторые преобразования: Пусть исходная ЗЛП имеет канонический вид (1). Подставим выражения базисных переменных (2) в целевую функцию. Получим:
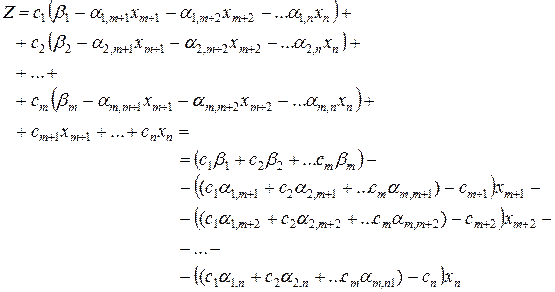
Введем обозначения:
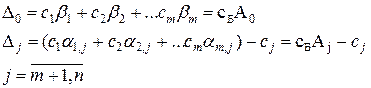
где
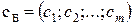 – вектор коэффициентов целевой функции;
– вектор коэффициентов целевой функции;
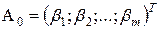 – вектор-столбец свободных членов;
– вектор-столбец свободных членов;
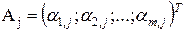 – вектор-столбец коэффициентов при переменных хj.
– вектор-столбец коэффициентов при переменных хj.
Таким образом задача исходная задача преобразуется в следующую:
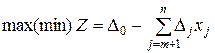
X= (x1, x2, … xn)
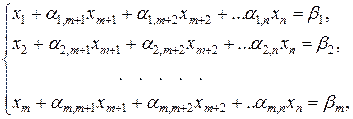 (3)
(3)
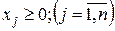
Такую задачу можно записать в виде симплексной таблицы:
| БП | сБ | х1 | х2 | ... | xi | ... | xm | xm+1 | ... | xj | ... | xn | А0 |
| c1 | c2 | ... | ci | ... | cm | cm+1 | ... | cj | ... | cn | |||
| х1 | c1 | 1 | 0 | ... | 0 | ... | 0 | α1,m+1 | ... | α1,j | ... | α1,n | β1 |
| х2 | c2 | 0 | 1 | ... | 0 | ... | 0 | α2,m+1 | ... | α2,j | ... | α2,n | β2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| xi | ci | 0 | 0 | ... | 1 | ... | 0 | αi,m+1 | ... | αi,j | ... | αi,n | βi |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| xm | cm | 0 | 0 | ... | 0 | ... | 1 | αm,m+1 | ... | αm,j | ... | αm,n | βm |
| Δj | 0 | 0 | ... | 0 | ... | 0 | Δm+1 | ... | Δj | ... | Δn | Δ0 | |
В симплексной таблице
- Последнюю строку в таблице называют индексной строкой (или строкой целевой функции);
- Число 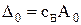 – значение целевой функции для начального опорного плана;
– значение целевой функции для начального опорного плана;
- Числа 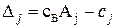
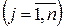 – называют индексными оценками свободных переменных.
– называют индексными оценками свободных переменных.
Теорема (признак оптимальности опорного плана):
Если для некоторого опорного плана все оценки при решении задачи на максимум не отрицательны, а при решении задачи на минимум – не положительны, то такой план оптимален.
Пример:
Некоторое предприятие выпускает столы и стулья. На изготовление одного стула стоимостью 1 у.д.е. требуется 1 куб.м сосны и 1 куб.м дуба, а для производства стола стоимостью 4 у.д.е. требуется 2 куб.м сосны. На складе имеется 100 куб.м сосны и 40 куб.м дуба.
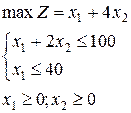
Решение:
Сведем к задаче в канонической форме:
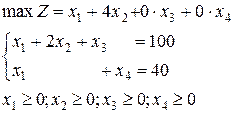
Составляем симплексную таблицу (х3 и х4 - базисные):
| БП | сБ | х1 | х2 | х3 | х4 | А0 |
| 1 | 4 | 0 | 0 | |||
| х3 | 0 | 1 | 2 | 1 | 0 | 100 |
| х4 | 0 | 1 | 0 | 0 | 1 | 40 |
| Δj | -1 | -4 | 0 | 0 | 0 | |
X= (0; 0| 100; 40)
План не оптимальный так как есть индексные оценки отрицательные.
Переход к не худшему плану.
Если опорный план не удовлетворяет критерию оптимальности, необходимо перейти к не худшему плану при помощи разрешающего элемента.
Столбец, индексная оценка которого является отрицательной при решении задачи на максимум (положительной при решении задачи на минимум) и максимальной по модулю, является разрешающим столбцом. (определяет переменную вводимую в базис)
Для того, чтобы определить индексную строку необходимо найти для каждой строки наименьшее симплексное отношение: 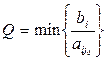 , где j0 – разрешающий столбец.
, где j0 – разрешающий столбец.
Строка, соответствующая наименьшему симплексному отношению называется разрешающей строкой. (определяет переменную выводимую из базиса, ее место в базисном плане займет вводимая переменная, см.пример в таблицах ниже)








