3. 2 реттеу жҮйесініҢ статикалыҚ сипаттамалар

Дата: 2025-06-02; Просмотры: 9
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0
 


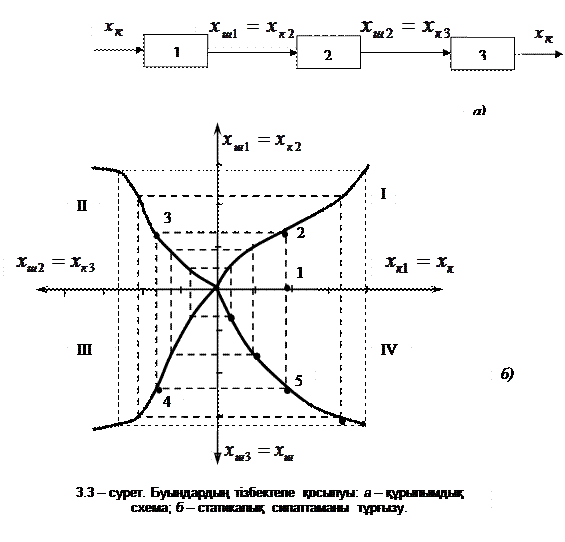Екі және одан да көп элементтердің тізбектеле қосылуы. Бұл жағдайда бір элементтің шығысы екінші элементтің кірісі болып буындар тізбегін құрайды. 3.3 – суретте үш тізбектеле қосылған буындардан тұратын жүйенің статикалық сипаттамасын салудың графикалық әдісі көрсетілген. Бірінші квадранттың абсцисса осіне бірінші буынның 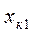, ал ординатасына — 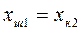мәндері салынады да, бұл квадрантта бірінші буынның статикалық сипаттамасын тұрғызамыз. Екінші квадранттың вертикаль осіне 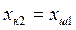, ал горизонталь осіне 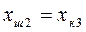мәндері салынып, бұл квадрантта екінші буынның сипаттамасы тұрғызылады. Үшінші квадранттың горизонталь осіне 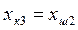, ал вертикаль осіне 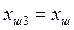мәндері салынып, үшінші квадрантта үшінші буынның статикалық сипаттамасы тұрғызылады.

Егер жүйе буындарының саны үштен көп болса, онда олар жеке-жеке топтарға бөлінеді де, әр топтың сипаттамалары ізделінеді. Соңынан әр топты бір буын деп альп, жүйенің толық сипаттамасы салынады. Егер жүйедегі буындар саны тек екеу-ақ болса, онда үшінші

квадранттағы буынды беріліс функциясы бірге тең, яғни сипаттамасы

биссектриса түрінде болатындай етіп алады.

Егер жүйе 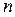сызықты буындардың тізбектеле қосылуынан тұратын болса оны сипаттайтын теңдеулер жүйесін төмендегі түрде көрсетуге болады:

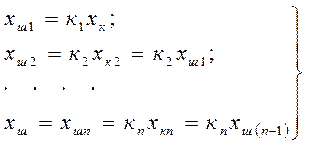(3.5)

Бұл теңдеулерден аралық 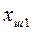, ,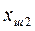..., 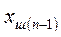координаттарын шығарып тастап мынаны аламыз:

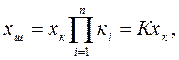(3.6)

мұндағы 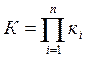– қосылыстың беріліс коэффициенті.

Сонымен, бағытталған сызықты буындардың тізбектеле қосылысының беріліс коэффициенті жеке буындар беріліс коэффициенттерінің көбейтіндісіне тең.

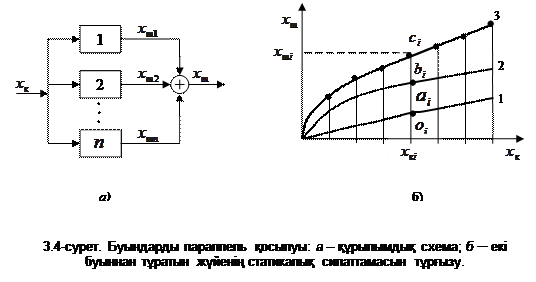
Буындардың параллель қосылуы. Буындар паралель қосылған кезде олардың кірістеріне бірдей 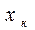сигналы беріледі де жүйенің 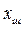сигналы буындардың шығыс сигналдарының қосындысынан тұрады. Бұл жағдайда буындарда әрекет бағыттылығы бар деп есептелінеді. Егер 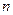параллель қосылған буындардың сипаттамалары белгілі болса

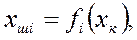
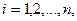
онда анықтамаға сәйкес шығыс сигналы

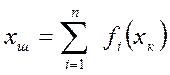. (3.7)

Жүйенің нәтижесіндегі статикалық сипаттамасы берілген 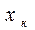мәніне сәйкес әр буынның статикалық сипаттамасының ординатасын бір-біріне қосу арқылы табылады. Оны салу әдісі (3.4) – суретте көрсетілген.

 

 

 


Кірістік сигнал 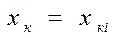болғанда

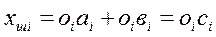
Параллель қосылатын сызықты буындар үшін буындар теңдеуі:

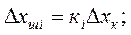
қосылыс теңдеуі:

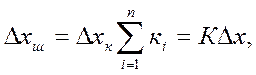(3.8)

мұндағы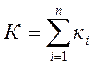

Бағытталған сызықты буындардың параллель қосылысының беріліс коэффициенті жеке буындар беріліс коэффициенттерінің қосындысына тең.

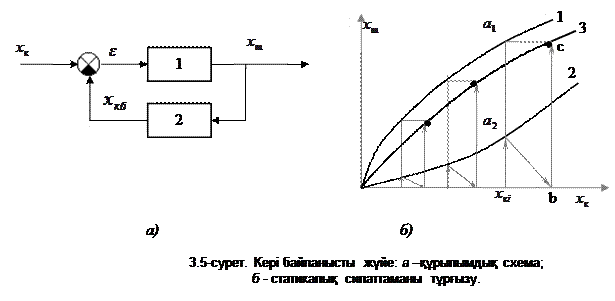
Кері байланыспен қамтылған жүйе. Бұл жағдайда буын бір немесе бірнеше буындарға қарама-қарсы қосылады және ол буын арқылы шығыстық шаманың бір бөлігі кірістік шамаға беріледі. Мұндай буынды кері байланыс буыны деп, ал бүкіл схеманы – кері байланысты схема деп атайды. Кері байланыспен қамтылған жүйенің статикалық сипаттамасын тұрғызудың графикалық жолы 3.5-суретте стрелкамен көрсетілген. 3.5, б-суретте 1-қисық кері байланысы жоқ 1-буынның сипаттамасы, ал 2-қисық кері байланыстағы 2-буынның сипаттамасы. Енді жүйенің толық сипаттамасын (3-қисық) алу үшін 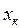осін тең бөліктерге бөліп а1, а2, в, с нүктелерін стрелкамен көрсеткен түзулерді тұрғызу арқылы тұрғызамыз.


Сызықты буынның беріліс коэффициенті 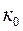, ал кері байланыстағы буынның беріліс коэффициенті 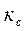болса 3.5,а – суреттен

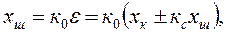
осыдан

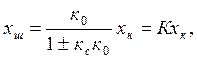(3.9)

мұндағы 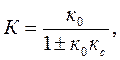аламыз. (3.10)

Бұл (3.9) және (3.10) теңдеулердің бөліміндегі „+” белгісі жүйеде оң, ал „-” таңбасы теріс кері байланыс бар екенін көрсетеді.

Егер кері байланыс салдарынан жүйе кірісіндегі сигнал көбейсе оң кері байланыс, ал азайса – теріс кері байланыс болғаны. Теріс кері байланыс бар кезде жүйенің 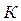беріліс коэффициенті әруақытта 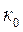коэффициентінен кіші; оң кері байланыста және 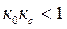болғанда әрқашан 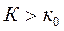; егер 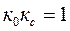болса 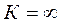. Іс жүзінде бұл кезде сызықтық буын астатикалық буынға, ал бейсызықты – релелік режимге ауысып кетеді.

 

3.3 РЕТТЕУ СТАТИЗМ І

 

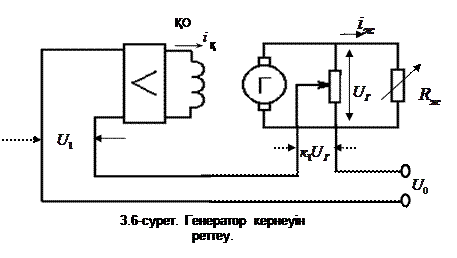
Реттеу объектісі тұрақты ток генераторы болсын (3.6 - сурет). Оның шығыстық 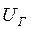кернеуі белгісіз делік.

 


Жүйенің орныққан режимі үшін:

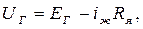(3.11)

мұндағы 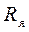-якорьдің кедергісі.

(3.11) теңдеуден жүктеме өскен сайын генератор кернеуінің азаятынын көреміз.

Генератордың бос жүріс режиміндегі электр қозғағыш күші:

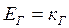i қ 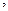(3.12)

мұндағы i қ – генератор қозу орамындағы ток. Ол

i қ 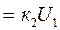(3.13)

теңдеуімен анықталады, мұндағы 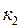- электрондық күшейткіштің күшейту коэффициенті. Ал,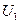

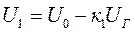(3.14)

теңдеуімен анықталатын күшейткіш кірісіндегі кернеу.

Енді алынған (3.11-3.14) теңдеулерін бірлестіре шешейік; нәтижесінде мына теңдеуді аламыз:

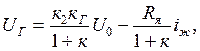(3.15)

мұндағы 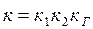- жүйенің күшейту коэффициенті.

Алынған (3.15) теңдеу генератор кернеуін автоматты реттеу жүйесінің статикалық режимдегі теңдеуі. Енді осы (3.15) теңдеуге талдау жүргізейік. Жүйе буындарының 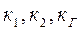коэффициентерін таңдай отыра генератордың бос жүріс ЭҚК үшін төмендегі теңдікті алуға болады:

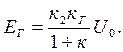(3.16)

Олай болса (3.15) теңдеуді мынандай етіп жазамыз:

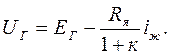(3.17)

(3.17) теңдеуді (3.11) теңдеуімен салыстыра отырып, 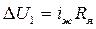- жүктеме өзгерген кезде реттеуіші жоқ жүйедегі генератор кернеуінің кему шамасы, 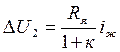- жүктеме өзгергендегі реттеуіші бар жүйедегі генератор кернеуінің кему шамасы екенін көреміз. Іс жүзіндегі жүйелер үшін әрқашан 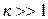болғандықтан, жүйеге реттеуішті енгізу статикалық қателікті 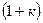есе азайтатынын байқауға болады.

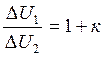немесе 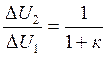(3.18)

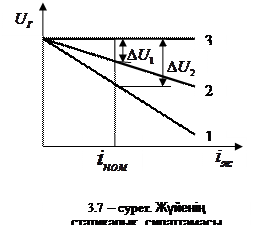
Яғни жүйенің күшейту коэффициенті ұлғайған сайын оның статикалық кателігі азаяды. 3.7 – суретте 1-түзу жүйенің реттеуіші жоқ кезіндегі сипаттамасы, 2-түзу жүйеге реттеуіші енгізілгендегі сипаттама, ал 3-түзу идеал жүйе сипаттамасы. Суреттен әр түрлі режимдегі 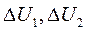реттеу қателіктерін көруге болады.

Реттеу статизмі немесе реттеудің біркелкі еместігі деген түсінік енгізсек, онда оны біздің жүйе үшін былай анықтауға болады:

яғни реттеуіші жоқ жүйе үшін

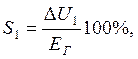
бұдан .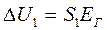

Реттеуіші бар жүйе үшін

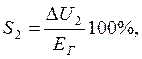
бұдан 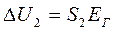. Яғни

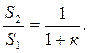(3.19)

Жалпы реттеу объектісі үшін 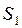мәні алдын-ала белгілі, ал 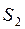мәні реттеу жүйесіне қойылатын техникалық шарттарға сәйкес беріледі. (3.19) формуладан реттелетін шаманы берілген дәлдікте қамтамасыз ететін жүйенің керекті күшейту коэффициентін анықтауға болады:

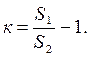(3.20)

Практикалық есептеуде

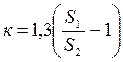
формуласын пайдаланады, мұндағы 1,3 – қор коэффициенті.

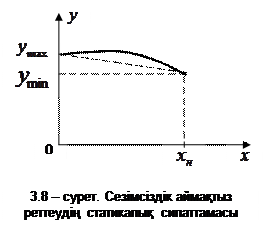Жалпы жағдайда реттеу статизмін төмендегідей түсіндіруге болады. Реттеу сипаттамасы 3.8 – суреттегідей берілген делік және ол 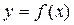теңдеуімен өрнектеледі делік. 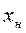- номинал жүктеме; 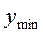- оған сәйкес реттелетін шаманың мәні; ал 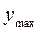- бос жүріс кезіндегі реттелетін шаманың мәні.

Салыстырмалы ауытқулар белгілеулерін енгізейік:

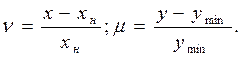(3.21)

Сипаттаманың кез-келген нүктесіндегі салыстырмалы еңістігін реттеудің осы нүктедегі статизмі деп атайды.

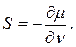
Егер бұл жағдайда сипаттама түзу сызық түрінде болса, онда

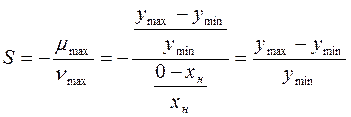(3.22)