3 -тарау . Автоматты басҚару жҮйесініҢ статикасы
3.1. СТАТИКАЛЫҚ СИПАТТАМАЛАР ЖӘНЕ СТАТИКАЛЫҚ БУЫНДАР
Автоматты басқару жүйелерінің, олардың жеке буындарының және қосылыстарының қасиеттері олардың сипаттамаларымен айқындалады.
Сипаттамалар статикалық және динамикалық болып келеді. Статикалы қ сипаттамалар буынның не жүйенің орныққан күйдегі шығыстық және кірістік шамаларының арасындағы тәуелділікті анықтайды.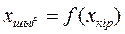 
(3.1)
Статикалық сипаттамалары бар жүйе буындары статикалық делінеді. Статикалық буындар не қосылыстар түріндегі автоматтық реттеу объектілері статикалық деп аталады. Оларды өздігінен түзелетін объектілер деп те атайды, өйткені олардың кірісіне келетін тұрақты әсерден реттелетін (шығыстық) шама белгілі бір тұрақты мәнге дейін ғана өсіп, одан ары жаңа деңгейде тұрақтанады, мұны реттеуші болмаған жағдайда объектінің өзі жүзеге асырады.
Жоғарыдағы (3.1) өрнегін буынның статикалық теңдеуі деп атайды, ал оған сәйкес келетін график статикалық сипаттаманы кескіндейді.
Егер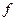 
функциясының өзі үзіліссіз және әр нүктесінде үзіліссіз туындылары болатын болса статикалық сипаттама аналитикалық деп аталынады. Бұл сипаттамалар сыптығыр қисық түрінде болады. Аналитикалық статикалық сипаттамалардың дербес түріне теңдеуі түзу сызықтыкіндей
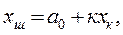(3.2)
мұндағы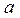 
және 
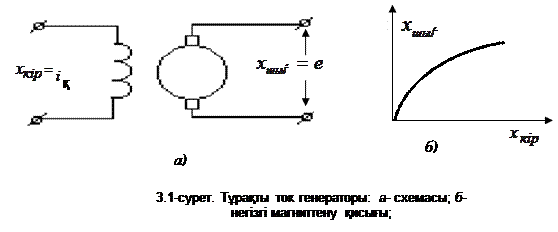
─ тұрақты коэффициенттер, болатын сызықтық статикалық сипаттама жатады. Мұндағы шамасын беріліс коэффициенті немесе буынның күшейту коэффициенті деп атайды. Сызықты статикалық сипаттамасы бар инерциясыз буынды сызықты статикалық буын деп атайды. Буынның аналитикалық сипаттамасының мысалы ретінде электрлік генератордың негізгі магниттену қисығын алуға болады (3.1-сурет). Бейаналитикалық статикалық сипаттамалардың не шығыс координатасының өзінде, не оның туындысында үзік жері болады. Мұндай сипаттамалардың мысалы ретінде кәдімгі реленің сипаттамасын алуға болады.
Астатикалық буындар. Жүйелерде кірістік және шығыстық шамаларының арасында өзара қатынас тағайындалмаған буындар болуы мүмкін. Оған мысал ретінде кірістік шамасы ретінде кернеу, ал шығыстық шама ретінде зәкірдің бұрылу бұрышы алынған электрқозғалтқышын алуға болады. Электр қозғалтқышқа тұрақты
 |
кернеу бергенде, зәкірдің бұрылу бұрышы белгілі бір жылдамдықпен үлкейе түседі. Мұндай буында статикалық сипаттамалар болмайды. Статикалық сипаттамасы жоқ буындар астатикалық деп аталады. Кейбір астатикалық буындар үшін тұрақты ретінде бірінші ретті туынды емес екінші, үшінші т. с. с. ретті туындылар болады. Бұл жағдайда буынды екінші, үшінші т. с. с. ретті астатизмді деп атайды. Астатикалық буындардың тұтастай жүйенің де белгісінің біріне беріліс функциясының бөліміндегі көбейткіш ретінде р комплекс айнымалының болуы жатады. Буынның не жүйенің беріліс функциясындағы 
коэффициенттері нөлге тең болса, онда беріліс функциясы мына түрде болады:
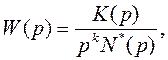(3.3)
мұндағы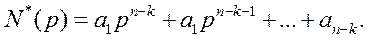 
Астатикалық объектілерді кейде өздігінен түзетілмейтін объектілер деп атайды, өйткені кіріске тұрақты әсер берілгенде реттелетін (шығыстық) шаманың мәні теория жүзінде шексіздікке өсе береді. Астатикалық буын түрінде болатын автоматты реттеу объектілері немесе олардың қосылыстары астатикалық деп аталады.
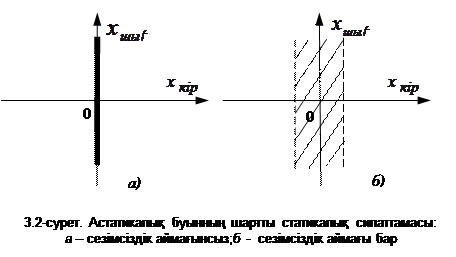
Астатикалық буындардың әсер жоқ кездегі орнықтылық күй аймағын геометриялық кескінмен көрсетуге болады. Шартты түрде бұл
|
аймақты „статикалық сипаттама” деп атайды. Мұндай буынның статикалық сипаттамасы ордината осіне дәл келеді (3.2,а-сурет). Егер буында сезімсіздік аймағы бар болса (мысалы, электроқозғалтқыш бастапқы күйінен тек кернеу кейбір мәнінен асқан кезде ғана қозғалады), онда орнықтылық күйінің геометриялық орны штрихтелген аймақ болады (3.2,б-сурет).
Сызықтық статистикалық сипаттаманың теңдеуін түрлендірген кезде оған координаттардың абсолют мәндерін емес, олардың бастапқы бір мәндерінен ауытқуын енгізеді. Бұл жағдайда статика теңдеуі мына түрде болады:
 |
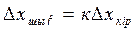, (3.4)
мұндағы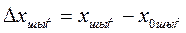 
;
,
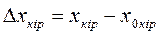ал бастапқы мәндері алғашқы (3.2) теңдеуін де қанағаттандырады:
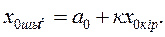
Бұл жағдайда статикалық сипаттама координата басынан өтетін түзу сызықпен кескінделеді.