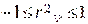Для опису неперервної ВВ використовують або функцію розподілу, або щільність ймовірностей.
Функцією розподілу ВВ 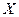 називають функцію
називають функцію 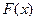 , що визначає ймовірність того, що ВВ
, що визначає ймовірність того, що ВВ 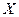 приймає значення менш, ніж
приймає значення менш, ніж 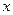 , тобто
, тобто 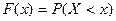 .
.
Щільністю ймовірності неперервної ВВ 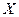 називають функцію:
називають функцію:
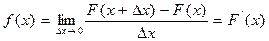 . (2)
. (2)
Для неперервних ВВ найбільш вивчені наступні закони розподілу: нормального розподілу, розподілу 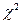 , Стьюдента, Фішера. Для зручності використання цих законів розроблені статистичні таблиці.
, Стьюдента, Фішера. Для зручності використання цих законів розроблені статистичні таблиці.
У багатьох практичних випадках інформація про ВВ, що дає закон розподілу є надмірною. Іноді вигідніше користатися числовими характеристиками ВВ.
53. Що таке генеральна сукупність, вибірка?
Генеральною сукупністю називається безліч усіх можливих значень досліджуваної ВВ 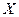 при заданих умовах. Вибіркою називають частину генеральної сукупності, яка відібрана для вивчення. Число елементів розглянутої сукупності називається обсягом.
при заданих умовах. Вибіркою називають частину генеральної сукупності, яка відібрана для вивчення. Число елементів розглянутої сукупності називається обсягом.
Числовими характеристиками ВВ 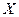 із вибірки обсягом
із вибірки обсягом 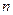 є:
є:
1. Вибіркове середнє – середнє арифметичне значень вибірки:
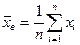 (9)
(9)
2. Вибіркова дисперсія:
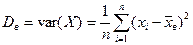 (10)
(10)
3. Вибіркове середнє квадратичне відхилення:
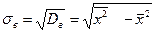 (11)
(11)
Надалі будемо позначати 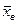 через
через 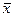 ,
, 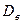 через
через 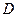 ,
, 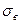 через
через 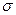 .
.
Для оцінки зв'язку двох ВВ 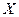 і
і 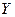 з вибірки обсягом
з вибірки обсягом 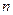 служать вибіркова коваріація
служать вибіркова коваріація 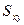 і вибірковий коефіцієнт кореляції
і вибірковий коефіцієнт кореляції 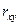 :
:
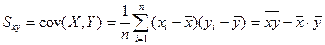 (12)
(12)
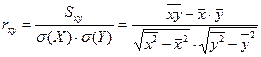 , (13)
, (13)
де 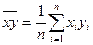 .
.
54. Як визначається і для чого використовується коефіцієнт кореляції?
Для оцінки лінійного кореляційного зв'язку між двома ознаками, що виміряні в метричних шкалах, часто використовують коефіцієнт кореляції Пірсона (його ще називають коефіцієнтом добутку моментів).
Коефіцієнт кореляції 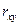 є відносною мірою зв'язку між двома факторами і завжди приймає значення в інтервалі
є відносною мірою зв'язку між двома факторами і завжди приймає значення в інтервалі 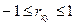 . Додатне значення коефіцієнта кореляції свідчить про прямий зв'язок між
. Додатне значення коефіцієнта кореляції свідчить про прямий зв'язок між 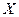 ,
, 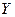 (зі зростанням однієї ВВ зростає середнє значення іншої), від’ємне – про зворотний зв'язок (зі зростанням однієї ВВ середнє значення іншої убуває). Якщо
(зі зростанням однієї ВВ зростає середнє значення іншої), від’ємне – про зворотний зв'язок (зі зростанням однієї ВВ середнє значення іншої убуває). Якщо 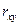 ®±1 – зв'язок тісний, якщо
®±1 – зв'язок тісний, якщо 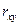 ®0 – лінійного зв'язку немає.
®0 – лінійного зв'язку немає.
Коефіцієнт кореляції Пірсона оцінює зв'язок між двома ознаками, лише припускаючи, що значення однієї ознаки пов'язані з відповідними середніми іншої ознаки лінійною залежністю, тобто оцінює лише лінійний за формою кореляційний зв'язок.
55. Як визначаються інтервали довіри для параметрів 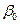 ,
, 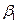 теоретичної лінійної регресії?
теоретичної лінійної регресії?
Для того, щоб виявити, як теоретичні параметри 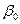 ,
, 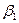 зв'язані з їх оцінками
зв'язані з їх оцінками 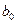 ,
, 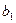 , необхідно визначити довірчі інтервали для параметрів теоретичної лінійної регресійної моделі, тобто такі інтервали, у які з заданою ймовірністю попадають їхні значення. Інтервали довіри для параметрів
, необхідно визначити довірчі інтервали для параметрів теоретичної лінійної регресійної моделі, тобто такі інтервали, у які з заданою ймовірністю попадають їхні значення. Інтервали довіри для параметрів 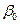 ,
, 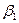 теоретичної регресії:
теоретичної регресії: 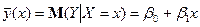 визначаються за формулами:
визначаються за формулами:
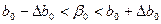 ,
, 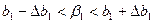 (5)
(5)
де 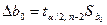 ,
, 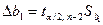 – граничні відхилення параметрів
– граничні відхилення параметрів 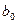 ,
, 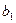 .
.
56. Як за результатами вибірки визначаються: вибіркове середнє, вибіркова дисперсія, вибіркове середнє квадратичне відхилення?
Означення.Вибірковою середньою або вибірковою зваженою середньоарифметичноюназивають середню арифметичну варіант вибірки із урахуванням їх частостей і позначають
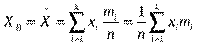 , де - об’єм вибірки, - кількість різних варіант,
, де - об’єм вибірки, - кількість різних варіант, 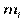 - частоти варіант
- частоти варіант 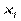 (
( 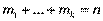 ). Аналогічно визначаєтьсягенеральна середня або генеральна зважена середньоарифметичнаіз заміною об’єму вибірки на
). Аналогічно визначаєтьсягенеральна середня або генеральна зважена середньоарифметичнаіз заміною об’єму вибірки на 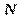 - об’єм генеральної сукупності і позначається
- об’єм генеральної сукупності і позначається 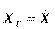 . Вибіркова середня є аналогом математичного сподівання і використовується дуже часто. Вона може приймати різні числові значення при різних вибірках однакового об’єму. Тому можна розглядати розподіли вибіркової середньої та числові характеристики цього розподілу. Неважко довести, що:
. Вибіркова середня є аналогом математичного сподівання і використовується дуже часто. Вона може приймати різні числові значення при різних вибірках однакового об’єму. Тому можна розглядати розподіли вибіркової середньої та числові характеристики цього розподілу. Неважко довести, що:
Теорема . Вибіркова середня є незсунутою, ефективною та обгрунтованою точковою оцінкою для генеральної середньої. Іншими словами, вибіркова середня є статистикою, яка задовольняє всі умови точкового оцінювання, для параметра – генеральної середньої кількісної ознаки.
Означення.Вибірковою дисперсією називають середню (зважену) квадратів відхилення варіант від вибіркової середньої:
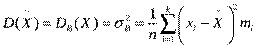 . Зауважимо, що для спрощення обчислення вибіркової дисперсії можна застосовувати формулу:
. Зауважимо, що для спрощення обчислення вибіркової дисперсії можна застосовувати формулу: 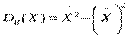 .
.
Означення.Вибірковим середньоквадратичним відхиленням (стандартом) називають квадратний корінь із вибіркової дисперсії 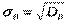 . Можна показати,що: Вибіркова дисперсія
. Можна показати,що: Вибіркова дисперсія 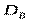 є ефективною, обгрунтованою, але ЗСУНУТОЮ точковою оцінкою для генеральної дисперсії
є ефективною, обгрунтованою, але ЗСУНУТОЮ точковою оцінкою для генеральної дисперсії 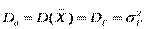 .
.
Зауваження. Вибіркова дисперсія дає занижені оцінки для генеральної дисперсії, але 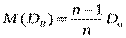 . Тому вибіркову дисперсію виправляють так, щоб вона стала незсунутою оцінкою. А саме, вводять так званувиправлену вибіркову дисперсію
. Тому вибіркову дисперсію виправляють так, щоб вона стала незсунутою оцінкою. А саме, вводять так званувиправлену вибіркову дисперсію
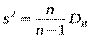 . Очевидно, що при достатньо великих об’ємах вибірки (
. Очевидно, що при достатньо великих об’ємах вибірки ( 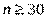 ) вибіркова дисперсія та виправлена вибіркова дисперсія різняться дуже мало, тому в практичних задачах виправлені вибіркові дисперсію та стандарт використовують лише при об’ємах вибірок
) вибіркова дисперсія та виправлена вибіркова дисперсія різняться дуже мало, тому в практичних задачах виправлені вибіркові дисперсію та стандарт використовують лише при об’ємах вибірок 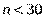 .
.
57. Як за результатами вибірки визначаються: вибіркові коефіцієнти коваріації та кореляції?
Коваріація – є мірою взаємозв’язку між 2 змішаними функціями, (незалежними або залежними). В економетричному аналізі використовують показник вибіркової коваріації, який дозволяє виразити залежність єдиним числом.
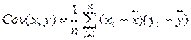
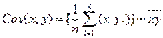
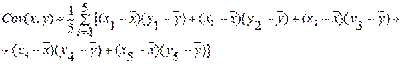
Більш точного мірою залежності х і у ніж Cov є коефіцієнт кореляції. Коефіцієнт кореляції вказує на тісноту зв’язку між залежними та незалежними змінними і дозволяє визначити кількісну оцінку між показниками і розраховується так:
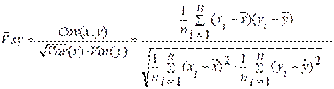
Коефіцієнт кореляції визначається як відношення коефіцієнта коваріації до коріння з 2-х дисперсій х і у.
Коефіцієнт кореляції на відмінну відкоефіцієнта коваріації є відносною мірою зв’язку. Таке значення коефіцієнта кореляції лежать в межах 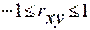 Позитивне значення коефіцієнта кореляції свідчить про прямий зв’язок між показниками, а негативне - про зворотній зв’язок.
Позитивне значення коефіцієнта кореляції свідчить про прямий зв’язок між показниками, а негативне - про зворотній зв’язок.
Коли коефіцієнт кореляції прямує за абсолютною величиною до f це свідчить про наявність сильного зв’язку між залежною і незалежною змінною, якщо прямує до 0 зв’язку немає.
Поряд з коефіцієнтом кореляції використовують коефіцієнт детермінації, за допомогою якого вимірюються щільність зв’язку між факторами.
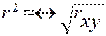 Значення коефіцієнта детермінації знаходиться в межах
Значення коефіцієнта детермінації знаходиться в межах