1. Критерій застосовується лише для тих моделей, що містять вільний член.

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

2. Передбачається, що випадкові відхилення 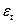визначаються за ітераційною схемою: 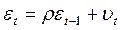, яка називається авторегресійною схемою першого порядку 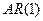, де 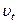– випадковий член.

3. Статистичні дані повинні мати однакову періодичність.

4. Критерій Дарбіна –Уотсона не застосовується для регресійних моделей, що містять у складі пояснюючих змінних залежну змінну з часовим лагом в один період, тобто для так званих авторегресійних моделей наступного виду:

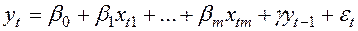
49. Тестування наявності мультиколінеарності. Алгоритм Фаррара-Глобера.

Найповніше дослідити мультиколінеарність можна за допомогою алгоритму Фаррара - Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється мультиколінеарність усього масиву незалежних змінних (за допомогою критерію c2), кожної незалежної змінної з рештою змінних (за допомогою F - критерію), кожної пари незалежних змінних (за допомогою t - критерію).

Опишемо алгоритм Фаррара - Глобера.

1. Проводять стандартизацію (нормалізацію) змінних за формулами:

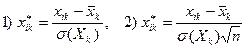де 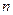- число спостережень; 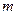- число пояснюючих змінних; 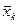- середнє арифметичне 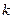-ї пояснюючої змінної ( 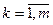); 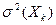- дисперсія 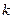-ї пояснюючої змінної.

2. Знаходять кореляційну матрицю:

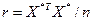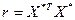1) ; 2) де 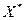- матриця стандартизованих незалежних (пояснюючих) змінних, 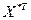- матриця, транспонована до матриці .

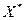3. Обчислюють критерій c2 :

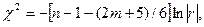де 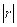— визначник кореляційної матриці .

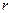Значення критерію 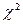порівнюється з табличним при 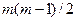ступенях вільності і рівні значущості 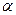. Якщо c2>c2табл то в масиві пояснюючих змінних існує мультиколінеарність.

4. Визначають обернену матрицю:

.

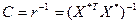5. Обчислюють F-критерії:

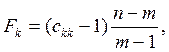де 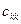- діагональні елементи матриці .

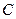Фактичні значення критеріїв 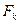порівнюються з табличними при 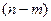і 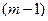ступенях свободи і рівні значущості 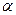. Якщо 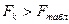, то відповідна 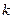-та незалежна змінна мультиколінеарна з іншими.

Розраховують коефіцієнт детермінації для кожної змінної:

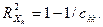
6. Знаходять частинні коефіцієнти кореляції:

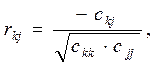де 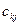- елемент матриці 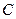, що міститься в 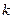-му рядку і 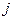-му стовпц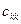і; і 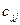- діагональні елементи матриці .

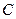7. Обчислюють t-критерії:

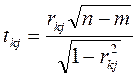Фактичні значення критеріїв 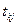порівнюються з табличними при 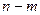ступенях свободи і рівні значущості 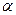. Якщо 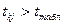, то між незалежними змінними 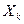і 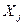існує мультиколінеарність.

50. У чому суть методу найменших квадратів (МНК)?

Можна показати, що властивості оцінок коефіцієнтів регресії ( 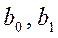), а також і якість побудованої регресії істотно залежать від властивостей випадкового відхилення ( 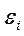). Доведено, що для одержання за МНК найкращих результатів необхідно, щоб виконувався ряд передумов щодо випадкового відхилення.

Передумови МНК (умови Гаусса – Маркова):

1°. Математичне сподівання випадкового відхилення 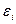дорівнює нулю: 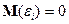для всіх спостережень.

2°. Дисперсія випадкових відхилень 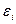постійна: 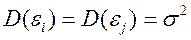для будь-яких спостережень 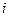і .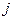

Здійсненність даної передумови називається гомоскедастичністю, нездійсненність – гетероскедастичністю.

3°. Випадкові відхилення 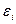і 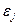є незалежними ( ):

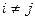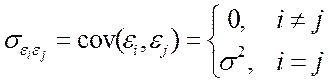
У випадку, якщо дана умова виконується, то говорять про відсутність автокореляції.

4°. Випадкове відхилення незалежне від пояснюючих змінних:

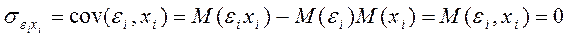(4)

5°. Модель є лінійною щодо параметрів.

Теорема Гаусса-Маркова. Якщо передумови 1° – 5° виконані, то оцінки, отримані за МНК, мають наступні властивості:

1. Оцінки є незміщеними, тобто , .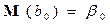

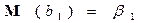2. Оцінки спроможні (обґрунтовані), тобто дисперсія оцінок параметрів при зростанні числа 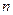спостережень прагне до нуля: ,.

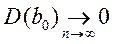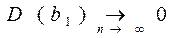
3. Оцінки ефективні, тобто вони мають найменшу дисперсію в порівнянні з будь-якими іншими оцінками даних параметрів, лінійними щодо величин .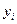

51. Часові ряди. Лагові змінні в економічних моделях.

Часов́ий ряд (англ. time series) — реалізація випадкового процесу, набір послідовних результатів спостереження. Приклади часових рядів кількість сонячних плям, сила вітру, змінення курсу валюти. Часовий ряд дуже часто побудовані за допомогою лінійних діаграм. Тимчасові ряди використовуються в статистиці, обробки сигналів, розпізнавання образів, економетрики, прогнозування погоди, передбачення землетрусів, електроенцефалографія, контроль інженерних даних, астрономії, інженерних комунікацій, і в значній мірі застосовується в наукових дослідженнях і техніки, який включає часові виміри.

Аналіз часових рядів включає методи аналізу часових рядів для того, щоб витягти корисну статистику та інші характеристики даних. Прогнозування часових рядів є використання моделі для прогнозування майбутніх значень на основі раніше спостережуваних значень. У той час як регресійний аналіз часто використовується таким чином, як для перевірки теорій, що поточні значення одного або більше незалежних часових рядів впливають на поточне значення іншої тимчасової серії, цей тип аналізу часових рядів не називається «Аналіз часових рядів», яка фокусується на порівнянні значень одного часового ряду або декількох залежних часових рядів в різні моменти часу.

Часові ряди. Лаги економічних моделей

Нехай для деякого економічного показника є послідовність значень в різні моменти часу: … , yt-k, …, yt-2, yt-1, yt, yt+1, … , yt+k, …

Динамічні моделі – моделі, в яких досліджується залежність між показниками в різні моменти часу або в якості пояснюючої змінної використовується час Т.

Лагові змінні – це змінні, вплив яких на залежну змінну характеризується певним запізненням.

Моделі із розподіленими лагами: в якості лагових змінних використовуються лише пояснюючі змінні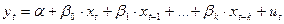

Авторегресійні моделі: в якості лагових змінних використовуються залежна змінна

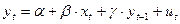
52. Що таке випадкова величина (ВВ)? Які види ВВ Вам відомі? Наведіть приклади дискретних та неперервних ВВ з економіки.

Ймовірністю події 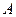( 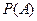) називається відношення числа 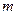елементарних подій, які сприяють появі події 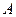до числа 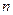всіх елементарних подій в умовах даного експерименту:

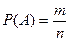(1)

При статистичному визначенні ймовірності події 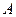під 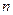розуміється кількість спостережень результатів експерименту, у яких подія 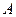зустрілася 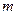раз.

Випадковою величиною (ВВ) називають величину, що у результаті спостереження приймає те чи інше значення, заздалегідь не відоме і залежне від випадкових обставин. Наприклад, обсяг ВНП, кількість реалізованої продукції, прибуток фірми і т.д.

Розрізняють дискретні і неперервні ВВ. Дискретною називають таку ВВ, що приймає окремі, ізольовані значення з визначеними ймовірностями. Неперервною називають таку ВВ, що може приймати будь-яке значення з деякого кінцевого чи нескінченого числового проміжку. Наприклад, можна вважати, що число покупців у магазині, які побували там протягом дня є дискретною ВВ. Однак більшість ВВ, розглянутих в економіці, мають настільки велике число можливих значень, що їх зручніше представляти у вигляді неперервних ВВ. Наприклад, курси валют, доход, обсяги ВНП, ВВП і т.п. розглядаються, як неперервні ВВ.

Дискретна ВВ задається так званим законом розподілу, який встановлює відповідність між усіма можливими значеннями ВВ і їхніми ймовірностями. Його можна задати табличне, аналітично або графічно.

При табличному завданні закону розподілу дискретної ВВ перший рядок таблиці містить її можливі значення 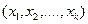, другий – їхні ймовірності 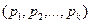. Обов'язково .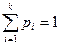