Сума квадратів, що пояснює регресію - SSR має тільки єдину незалежну одиницю інформації, яка утворюється з у1,...,у n, а саме b1. Доведемо це.
Запишемо відхилення, що пояснює регресію, у вигляді:
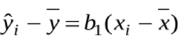
Візьмемо суми з обох боків рівняння і піднесемо їх до квадрату:
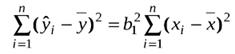
Таким чином, дійсно SSR можна утворити, використовуючи лише єдину незалежну одиницю інформації b1.
Сума квадратів помилок SSE має (n - 2) ступеня вільності:
SST = SSE + SSR
У разі простої лінійної регресії: n-1 = n-2 + 1
Ця сума базується на кількості ступенів вільності, яка дорівнює різниці між кількістю спостережень і кількістю параметрів, що оцінюються. У разі простої лінійної регресії оцінюються два параметри b0таb1. Якщо позначити кількість спостережень черезn, то дляSSE маємо (n- 2) ступеня вільності. Ступені вільності позначаються так:df або Df.
45. Сформулюйте означення функції регресії.
Регресі́йний ана́ліз — розділ математичної статистики, присвячений методам аналізу залежності однієї величини від іншої. На відміну від кореляційного аналізу не з'ясовує чи істотний зв'язок, а займається пошуком моделі цього зв'язку, вираженої у функції регресії.
Регресійний аналіз використовується в тому випадку, якщо відношення між змінними можуть бути виражені кількісно у виді деякої комбінації цих змінних. Отримана комбінація використовується для передбачення значення, що може приймати цільова (залежна) змінна, яка обчислюється на заданому наборі значень вхідних (незалежних) змінних. У найпростішому випадку для цього використовуються стандартні статистичні методи, такі як лінійна регресія. На жаль, більшість реальних моделей не вкладаються в рамки лінійної регресії. Наприклад, розміри продажів чи фондові ціни дуже складні для передбачення, оскільки можуть залежати від комплексу взаємозв'язків множин змінних. Таким чином, необхідні комплексні методи для передбачення майбутніх значень.
Мета регресійного аналізу
Визначення ступеня детермінованості варіації критеріальної (залежної) змінної предикторами (незалежними змінними).
Прогнозування значення залежної змінної за допомогою незалежної.
Визначення внеску окремих незалежних змінних у варіацію залежної.
Регресійний аналіз не можна використовувати для визначення наявності зв'язку між змінними, оскільки наявність такого зв'язку і є передумова для застосування аналізу.
46. Теоретичне, емпіричне рівняння багатофакторної регресії.
На будь-який економічний показник найчастіше впливає не один, а декілька факторів. У цьому випадку замість парної регресії розглядається багатофакторна регресія:
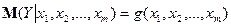(1)
Рівняння багатофакторної регресії може бути представлене у вигляді:
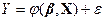(2)
де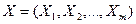 
– вектор незалежних (пояснюючих) змінних;
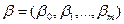– вектор невідомих параметрів;
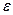– випадкове відхилення;
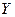– залежна (пояснювана) змінна.
Розглянемо найбільш просту з моделей багатофакторної регресії – модель багатофакторної лінійної регресії.
Теоретичне лінійне рівняння багатофакторної регресії має вигляд:
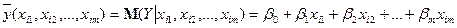(3)
Фактичні значення залежної змінної знаходяться за формулою:
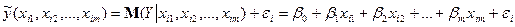
47. Теоретичне, емпіричне рівняння парної лінійної регресії.
При розрахунках параметрів моделі лінійної регресії як правило застосовується метод найменших квадратів, але також можуть бути використані інші методи. Так само метод найменших квадратів може бути використаний і для нелінійних моделей. Тому МНК та лінійна регресія хоч і є тісно пов'язаними, але не є синонімами.Моделі лінійної регресії знайшли найбільш широке використання в економічних дослідженнях, хоча це і є спрощений засіб в моделюванні реальних економічних процесів. Якщо в рівняння включено лише одну пояснюючу змінну, то одержуємо теоретичну модель, яка дістала назву парної лінійної регресії:
yі= β0+ β1x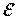i+ 
i
Теоретичну модель для парної лінійної регресії можна записати наступним чином: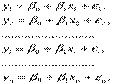 
або у векторно-матричній формі, співвідношення буде мати такий вигляд:
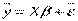де:
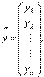
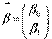
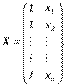
Для визначення теоретичних коефіцієнтів β0, β1необхідно буде використати всі значення (хі, уі) зміннихYі Х генеральної сукупності, що практично здійснити не можливо.
Тому переходимо до побудови так званого емпіричного рівняння на базі інформації одержаної із вибірки. Емпіричне рівняння регресії має вигляд:
48. Тестування наявності автокореляції залишків за критерієм Дарбіна-Уотсона.
Тестування методом Дарбіна –Уотсона складається з наступних етапів:
1. За побудованим емпіричним рівнянням регресії:
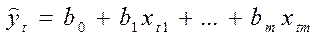
визначаються значення відхилень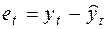 
для кожного спостереження 
, 
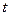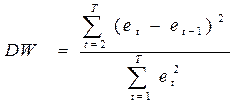
2. За формулою розраховується статистика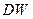 
.
3. За таблицею критичних точок Дарбіна – Уотсона визначаються два числа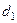 
й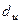 
і здійснюють висновки за правилами:
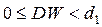– існує позитивна автокореляція,
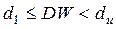– висновок про наявність автокореляції не визначений,
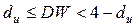– автокореляція відсутня,
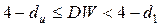– висновок про наявність автокореляції не визначений,
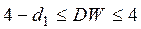– існує від’ємна автокореляція.
Відзначимо, що при використанні критерію Дарбіна –Уотсона необхідно враховувати наступні обмеження.