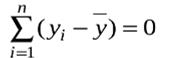Автокореляція може бути як позитивною, так і від’ємною. В економічних задачах значно частіше зустрічається так звана позитивна автокореляція ( >0), ніж від’ємна автокореляція ( <0).
Серед основних причин, що викликають появу автокореляції, можна виділити помилки специфікації, інерцію в зміні економічних показників, ефект павутини, згладжування даних.
Помилки специфікації. Неврахування в моделі якої-небудь важливої пояснюючої змінної або невірний вибір форми залежності звичайно приводить до системних відхилень точок спостережень від лінії регресії, що може обумовити автокореляцію.
Інерція. Багато економічних показників (наприклад, інфляція, безробіття, ВНП і т.п.) змінюється не миттєво, а з деяким часовим лагом.
Ефект павутини. Економічні показники реагують на зміну економічних умов із запізнюванням. Наприклад, пропозиція сільськогосподарської продукції реагує на зміну ціни з запізнюванням (рівним періоду дозрівання врожаю). Велика ціна сільськогосподарської продукції в минулому році викликає (швидше за все) її надвиробництво в поточному році, а отже, ціна на неї знизиться і т.д.
Згладжування даних. Найчастіше дані по деякому тривалому часовому періоду одержують усередненням даних по складовим його подінтервалам. Це може привести до визначеного згладжування коливань усередині розглянутого періоду, що у свою чергу може послужити причиною автокореляції.
Наслідки автокореляції:
1. Оцінки параметрів, залишаючись лінійними і незміщеними, перестають бути ефективними. Отже, вони перестають мати властивості найкращих лінійних незміщених оцінок (BLUE-оцінок).
2. Дисперсії оцінок є зміщеними. Часто дисперсії, що обчислюються по стандартних формулах, є заниженими, що спричиняє збільшення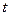 
-статистик. Це може привести до визнання статистично значимими пояснюючі змінні, котрі в дійсності такими можуть і не бути.
3. Оцінка дисперсії регресії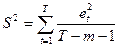 
є зміщеною оцінкою дійсного значення 
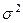у багатьох випадках занижуючи його.
4. Висновки по 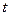- і 
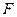-статистиках, що визначають значимість коефіцієнтів регресії і коефіцієнта детермінації, можливо, будуть невірними.
42. Сформулюйте означення багатофакторної лінійної регресії.
На будь-який економічний показник найчастіше впливає не один, а декілька факторів. У цьому випадку замість парної регресії розглядається багатофакторна регресія:
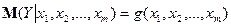(1)
Рівняння багатофакторної регресії може бути представлене у вигляді:
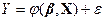(2)
де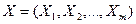 
– вектор незалежних (пояснюючих) змінних;
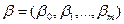– вектор невідомих параметрів;
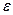– випадкове відхилення;
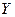– залежна (пояснювана) змінна.
Розглянемо найбільш просту з моделей багатофакторної регресії – модель багатофакторної лінійної регресії.
Теоретичне лінійне рівняння багатофакторної регресії має вигляд:
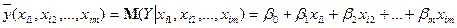(3)
Фактичні значення залежної змінної знаходяться за формулою:
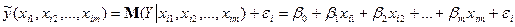(4)
43. Сформулюйте означення парної лінійної регресії.
Функціональна залежність умовного математичного сподівання 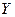від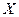 
називається функцією регресії 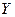на :
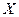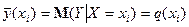(1)
де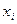 
– значення В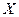В в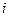 
-му спостереженні, 
.
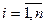Парна лінійна регресія являє собою лінійну функцію між умовним математичним сподіванням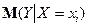 
залежної змінної 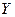і однією незалежною змінною :
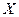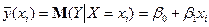. (2)
Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної (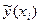 
) відхиляється від відповідного умовного математичного сподівання ( 
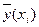), необхідно ввести в співвідношення (2) випадковий доданок 
:
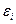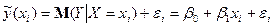, (3)
де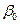 
, 
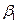– теоретичні параметри (теоретичні коефіцієнти) регресії;
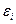– випадкові відхилення.
Співвідношення (3) називається теоретичною лінійною регресійною моделлю. За вибіркою можна побудувати емпіричне рівняння регресії:
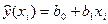, (4)
де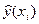 
– оцінка умовного математичного сподівання ;
, 
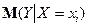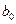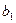– оцінки невідомих параметрів 
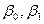(емпіричні коефіцієнти регресії).
Фактичні значення залежної змінної (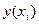 
) розраховуються за формулою:
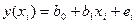, (5)
де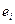 
– оцінка теоретичного випадкового відхилення .
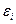44. Сформулюйте означення та наведіть формули для розрахунків SSR, SSE, SST. Ступені вільності величин SSR, SSE, SST.
SST – загальна сума квадратів яку прийнято позначати SST (sum square total)
SSE – сума квадратів помилок сума квадратів помилок, яка позначаєтьсяSSE (sum square error)
SSR – сума квадратів, що пояснюється регресією та позначаєтьсяSSR (sum square regression)
;
;
.
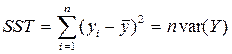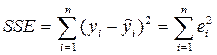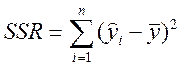Розглянемо тотожність, яка пов'язує загальну суму квадратів із сумою квадратів помилок та із сумою квадратів, що пояснюють регресію:
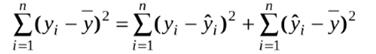
ST = SSE + SSR .
Кожна сума квадратів пов'язана з числом, яке називається її ступенем вільності, це число показує, скільки незалежних елементів інформації, які утворюються з елементів (у1,...,у n) потрібно для розрахунку даної суми квадратів.
Розглянемо, скільки ступенів вільності має кожна, вивчена нами сума квадратів.
Для утворення SST потрібно(n -1) незалежних чисел, тому що з чисел
{(y1 -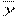 
), (y2 -), ... , (yn -)}незалежні тільки (n -1) завдяки властивості:
