31. Оцінка моделей з лаговими змінними. Перетворення Койка.
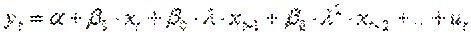
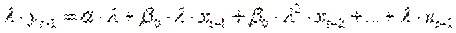
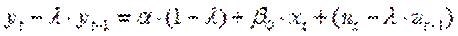
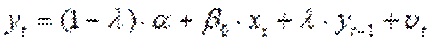
де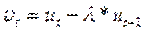 
- ковзка середня між 
.
Це перетворення знімає проблему мультиколінеарності і дозволяє аналізувати короткотермінові і довготермінові властивості змінних:
- у коротко термінованому періоді значення 
розглядається як фіксоване і короткотерміновий мультиплікатор = 
, а довго терміновий – обчислюється як сума нескінченно спадної геометричної прогресії. - у довго терміновому періоді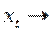 
до деякого свого рівнозваженого значення 
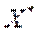, то значення 
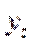і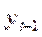 
теж прямують до свого рівноважного 
:
;
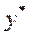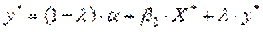
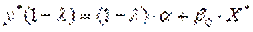
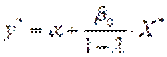- крім того як сума нескінченно спадної геометричної прогресії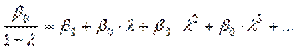 
є довготерміновим мультиплікатором;
- при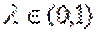 
довготерміновий вплив буде сильнішим за короткотерміновий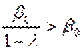 
Але: серед пояснюючих змінних є змінна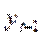 
, яка має випадковий характер, що порушує одну з передумов МНК, та ще й може корелювати із випадковими відхиленням 
.
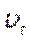32. Оцінка параметрів лінійного рівняння багатофакторної регресії за допомогою МНК.
Оцінка значущості параметрів лінійного рівняння багатофакторної регресії проводиться за наступним алгоритмом t - тесту Стьюдента:
1) для кожного параметра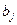 
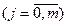розраховується t - відношення: 
,
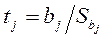де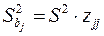 
- дисперсії оцінок коефіцієнтів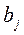 
;
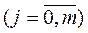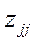- діагональний елемент матриці 
;
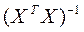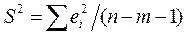- незміщена оцінка дисперсії відхилень,
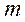- кількість пояснюючих змінних;
2) з таблиць критичних точок t - розподілу Стьюдента знаходять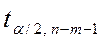 
;
3) якщо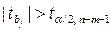 
- коефіцієнт 
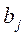є статистично значущим,
якщо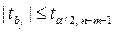 
- коефіцієнт 
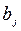вважається статистично незначущим і змінну 
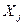рекомендується виключити з рівняння.
33. Оцінка параметрів парної лінійної регресії за допомогою МНК.
Для того, щоб мати явний вид залежності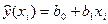 
,(4), необхідно оцінити невідомі параметри 
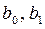. Для визначення параметрів 
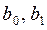застосовують метод найменших квадратів (МНК).
Можна припустити, що між даними існує лінійна залежність. У цьому випадку їх можна апроксимувати прямою лінією. Апроксимуюча пряма повинна проходити через точки таким чином, щоб сума квадратів помилок була мінімальною. Запишемо критерій найменших квадратів: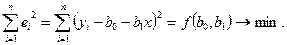 
(6)
Необхідними умовами екстремуму функції (6) є умови рівності нулю значень частинних похідних першого порядку: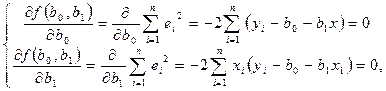 
(7)
З умов екстремуму функції (7) одержимо систему лінійних рівнянь:
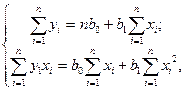(8)
З (8): 
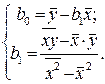(9)
де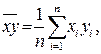 
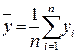
Запишемо рівняння прямої в наступному вигляді: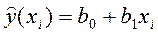 
,
34. Перевірка статистичної значущості коефіцієнтів b0 та b1 лінійної регресії за допомогою t-теста Стьюдента.
Для перевірки значущості параметрів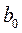 
, 
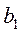парної лінійної регресії за t -тестом Стьюдента необхідно:
1) розрахувати t - відношення: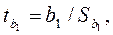 
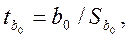
де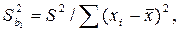 
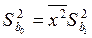- дисперсії параметрів 
, 
;
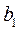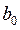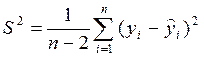- незміщена оцінка дисперсії відхилень;
2) з таблиць критичних точок розподілу Стьюдента знайти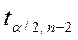 
( 
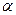- рівень значущості);
3) якщо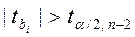 
- коефіцієнт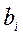 
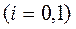є статистично значущим.
Для перевірки статистичної значущості коефіцієнта кореляції за t-тестом Стьюдента необхідно:
1) розрахувати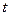 
-відношення: 
;
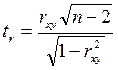2) з таблиць критичних точок розподілу Стьюдента знайти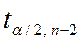 
;
3) якщо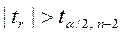 
- коефіцієнт 
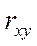є статистично значущий.
35. Передумови МНК, теорема Гаусса -Маркова.
Можна показати, що властивості оцінок коефіцієнтів регресії (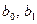 
), а також і якість побудованої регресії істотно залежать від властивостей випадкового відхилення ( 
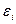). Доведено, що для одержання за МНК найкращих результатів необхідно, щоб виконувався ряд передумов щодо випадкового відхилення.
Передумови МНК (умови Гаусса – Маркова):
1°. Математичне сподівання випадкового відхилення 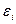дорівнює нулю: 
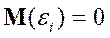для всіх спостережень.
2°. Дисперсія випадкових відхилень 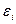постійна: 
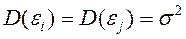для будь-яких спостережень 
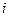і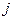 
.
Здійсненність даної передумови називається гомоскедастичністю, нездійсненність – гетероскедастичністю.
3°. Випадкові відхилення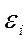 
і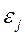 
є незалежними ( 
):
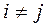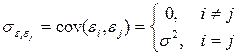(3)
У випадку, якщо дана умова виконується, то говорять про відсутність автокореляції.
4°. Випадкове відхилення незалежне від пояснюючих змінних:
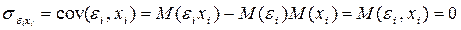(4)
5°. Модель є лінійною щодо параметрів.
Теорема Гаусса-Маркова. Якщо передумови 1° – 5° виконані, то оцінки, отримані за МНК, мають наступні властивості:
1. Оцінки є незміщеними, тобто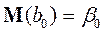 
, 
.
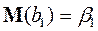2. Оцінки спроможні (обґрунтовані), тобто дисперсія оцінок параметрів при зростанні числа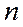 
спостережень прагне до нуля: 
, 
.
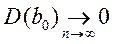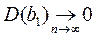3. Оцінки ефективні, тобто вони мають найменшу дисперсію в порівнянні з будь-якими іншими оцінками даних параметрів, лінійними щодо величин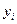 
.
В англомовній літературі такі оцінки називаються BLUE – найкращі лінійні незміщені оцінки. Якщо передумови 2° і 3° порушені, то властивості незміщеності і спроможності зберігаються, а властивість ефективності – ні.
36. Поняття гетероскедастичності та її наслідки.
Однією з таких передумов МНК є умова сталості дисперсій випадкових відхилень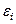 
:
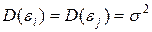для будь-яких спостережень 
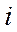і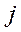 
.
Якщо дана передумова виконується, то має місце гомоскедастичністъ (сталість дисперсії відхилень). Невиконання даної передумови називається гетероскедастичністю (дисперсія відхилень не є сталою). Наведемо приклади гомо- і гетероскедастичності на рис. 1, 2 .
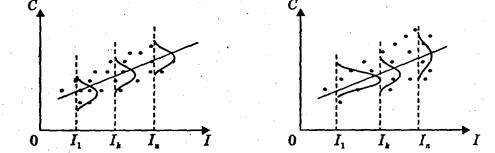
Рис. 1 Гомоскедастичність Рис. 2 Гетероскедастичність
37. Поняття мультиколінеарності та її наслідки .
Мультиколінеарність означає існування тісної лінійної залежності, або сильної кореляції, між двома чи більше пояснюючими змінними.
Наслідки мультиколінеарності:
1) великі дисперсії (стандартні помилки) оцінок теоретичних параметрів;
2) зменшуються t - статистики коефіцієнтів, що може привести до невірного висновку про вплив відповідної пояснюючої змінної на залежну змінну;
3) оцінки теоретичних параметрів і їхні стандартні помилки стають дуже чуттєвими до найменшої зміни даних, тобто вони стають нестійкими;
4) можливе одержання невірного знака коефіцієнта регресії.