Пуассонівський закон розподілу – це закон розподілу випадкової величини, заданий таблицею, у якій ймовірність обчислюється за формулою Пуассона

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

12. Дайте означення коваріації.

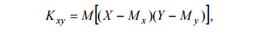Коваріація визначає взаємозв’язок випадкових величин:

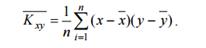а відповідна оцінка розраховується за формулою:

1 . Функція Кxy визначає величину статистичного зв’язку між двома випадковими величинами X, Y. Коваріація тим більша, чим більше ймовірність того, що із збільшенням однієї величини збільшиться й друга. Коваріація характеризує ступінь лінійної залежності між випадковими величинами. Коваріація є розмірною величиною і може набувати будь-яких значень. Це не дозволяє, знаючи величину коваріації, оцінити, великий чи малий ступінь зв’язку між змінними. Тому вона не набула такого поширення у статистичному аналізі, як кореляція.

13. Дайте означення середнього квадратичного відхилення ВВ.

Середнє квадратичне відхилення (позначається літерою s) є квадратним коренем із дисперсії.

Якщо від випадкової величини віднімемо її математичне сподівання, то дістанемо центровану випадкову величину, математичне сподівання якої дорівнює нулю. Ділення випадкової величини на її середнє квадратичне відхилення називається норму­ванням цієї випадкової величини.

Середнє лінійне відхилення – величина іменована і визначається за формулами:

а) середнє лінійне відхилення просте

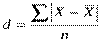
б) середнє лінійне відхилення зважене

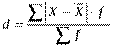
14. Дайте означення та перелічите основні властивості математичного сподівання ВВ.

Математичним сподіванням дискретної випадкової величини , яка набуває значень із скінченної множини чисел , називається число

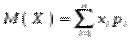
яке дорівнює сумі добутків значень випадкової величини на відповідні ймовірності.

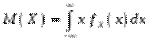Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число

Математичне сподівання випадкової величини має такі властивості.

1.Математичне сподівання сталої випадкової величини дорівнює цій величині.(Мс = с, де с = const).

2.Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань. (M(X + Y) = MX + MY).

3.Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань. (M(X × Y)=MX × MY).

4.Сталу величину можна виносити за знак математичного сподівання. (M(сX) = сMX, де с = const).

5.Математичне сподівання відхилення випадкової величини від свого математичного сподівання дорівнює нулеві. (М(Х – МХ) = 0).

15. Дайте означення функції розподілу ВВ.

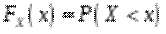Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподіл величини : значення цієї функції в точці 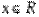дорівнює ймовірності того, що випадкова величина набуває значення менше :

Оскільки функція розподілу являє собою ймовірність, вона повинназадовольняти основним аксіомам теорії ймовірностей і мати властивості, притаманні ймовірностям. Але ця функція залежить від можливих значень випадкової величини , і тому повинна в загальному вигляді визначатися для всіх значень . Таким чином, вимога, щоб функція розподілу являла собою ймовірність, накладає на її властивості певні обмеження.

Основні властивості функції розподілу довільної випадкової величини :

1) , ;

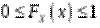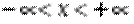2) , ( , )

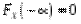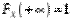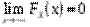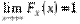3) Функція не зменшується при зростанні (неспадна, тобто 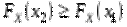, якщо .)

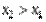4) .

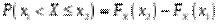Відзначимо ще одну властивість функції :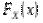

5) Якщ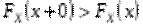о , то

,

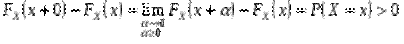тобто стрибок функції в довільній точці 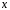збігається з ймовірністю події .

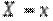16. Дайте означення функції щільності ймовірності неперервної ВВ.

Для неперервних випадкових величин поряд із законом розподілу ймовірностей розглядають густину (щільність) імовірностей, яку позначають так f(x). Щільністю розподілу ймовірності неперервної випадкової величини називається функція f(x), що є першою похідною від інтегральної функції розподілу ймовірності F(x) f (x) = F ′(x).

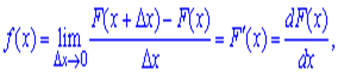звідки диференціал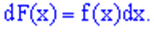

Оскільки приріст визначають залежністю

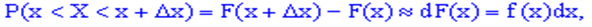
то добуток щільності ймовірностей на приріст випадкової величини f(x)dx відповідає ймовірність того, що випадкова величина X міститиметься у проміжку [x; x+dx], де dx це приріст .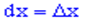

Геометрично на графіку щільності ймовірностей f(x)dx відповідає площа прямокутника з основою dx і висотою f(x)

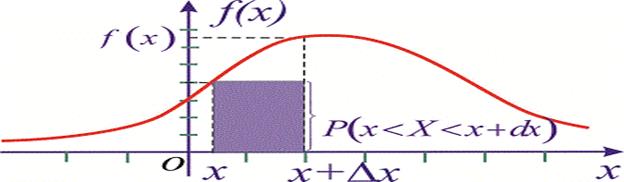
Щільність розподілу f(x) неперервної випадкової величини успадковує усі властивості інтегральної функції розподілу F(x).

Властивості щільності розподілу:

Властивість 1. Інтеграл у нескінченних границях від щільності розподілу

дорівнює одиниці (умова нормування) 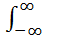f (x )dx = 1 .

Властивість 2. Щільність розподілу – функція невід’ємна f (x) ≥ 0 .

Оскільки її первісна F(x) є неспадною функцією.

Властивість 3.Імовірність попадання неперервної випадкової величини в проміжок [а,b) визначається залежністю 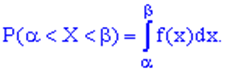4. Функція розподілу ймовірностей неперервної випадкової величини визначається через щільність розподілу ймовірностей інтегруванням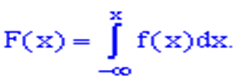

17. Зв’язок між коефіцієнтом кореляції та коефіцієнтом детермінації.

Поряд з коефіцієнтом кореляції використовується ще один критерій, за допомогою якого також вимірюється щільність зв'язку між двома або більше показниками та перевіряється адекватність (відповідність) побудованої регресійної моделі реальній дійсності. Тобто дається відповідь на запитання, чи дійсно зміна значення у лінійно залежить саме від зміни значення х, а не відбувається під впливом різних випадкових факторів. Таким критерієм є коефіцієнт детермінації.

Щоб пояснити, що саме являє собою коефіцієнт детермінації та як він пов'язаний з коефіцієнтом кореляції, розглянемо питання про декомпозицію дисперсій.

Розглянемо на рисункі, як розбиваються на дві частини відхилення фактичних (емпіричних) значень залежної змінної від значень, які знаходяться на регресійній прямій (теоретичних 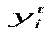або розрахункових ):

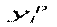Як видно із рисунка: 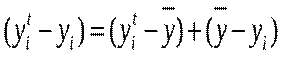. Звідси дістаємо

. (*)

В статистиці різницю прийнято називати загальним відхиленням. Різницю називають відхиленням, яке можна пояснити, виходячи із регресійної прямої. Різницю називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням. Піднесемо обидві частини (*) до квадрату і підсумуємо по. Враховуючи, що сума похибок дорівнює нулю, дістанемо: , (**)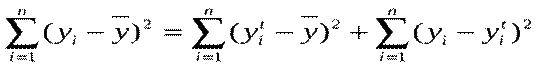

Поділивши обидві частини (*) на , отримаємо так зване «правило складання дисперсій»:

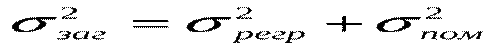,(***) Таким чином, ми розклали загальну дисперсію на дві частини: дисперсію, що пояснює регресію, та дисперсію помилок (або дисперсію випадкової величини). Поділимо обидві частини (***) на 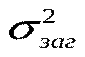і отримаємо:

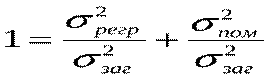Як видно, перше відношення у правій частині є пропорцією дисперсії, що пояснює регресію, у загальній дисперсії. Друге відношення є пропорцією дисперсії помилок у загальній дисперсії, тобто є частиною дисперсії, яку не можна пояснити через регресійний зв’язок.

Частина дисперсії, що пояснює регресію, називається коефіцієнтом детермінації і позначається 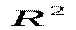. Коефіцієнт детермінації використовується як критерій адекватності моделі, оскільки є мірою пояснювальної сили незалежної змінної . Коефіцієнт детермінації можна записати в одному із двох еквівалентних виразів:

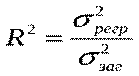або 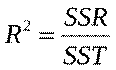. 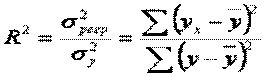Очевидно, що 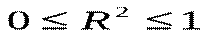. Враховуючи, що коефіцієнт кореляції 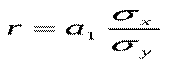, неважко встановити наступний зв’язок між коефіцієнтами детермінації та кореляції (для лінійної регресії):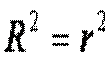

Отже коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції.

18. Зв’язок між коефіцієнтом кореляції та кутовим коефіцієнтом b₁.

Який зв’язок існує між коефіцієнтом кореляції і нахилом прямої регресії b1. Нагадаємо, що: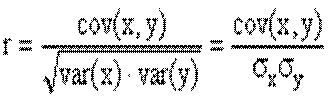

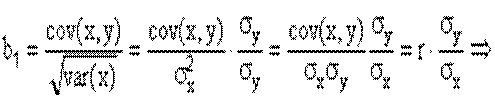
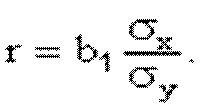
Так як значення додатні, то знак коефіцієнта кореляції завжди збігається із знаком параметра b1. Знак коефіцієнта кореляції співпадає із знаком коефіцієнта b1 в рівнянні регресії. Коефіцієнт кореляції знаходиться в межах від 0 до ±1. Якщо коефіцієнт кореляції дорівнює нулю, то зв'язок відсутній, а якщо одиниці, то зв'язок функціональний. Знак при коефіцієнті кореляції вказує на напрям зв'язку ("+" - прямий, "-" - обернений). Знак коефіцієнта показує "напрямок" зв'язку. Додатний коефіцієнт кореляції (r > 0) свідчить про "прямий" зв'язок між ознаками (тобто такий, коли збільшення значення однієї ознаки збільшує значення іншої ознаки), а від'ємний (г < 0) — про "зворотний" зв'язок (такий, коли зростання однієї ознаки веде до зменшення іншої ознаки). Чим ближче коефіцієнт кореляції до одиниці, тим зв'язок між ознаками тісніший.

19. Методи пом’якшення гетероскедастичності.

Гетероскедастичність призводить до неефективності оцінок, незважаючи на їх незміщеність. Це може призвести до необґрунтованих висновків щодо якості моделі. Тому при встановленні гетероскедастичності виникає необхідність перетворення моделі з метою усунення даного недоліку. Вид перетворення залежить від того, відомі чи ні дисперсії відхилень. Метод зважених найменших квадратів (ВНК)

Даний метод застосовується при відомих для кожного спостереження значеннях . У цьому випадку можна усунути гетероскедастичність, розділивши кожне значення, що спостерігається на відповідне йому значення дисперсії. У цьому суть методу зважених найменших квадратів.

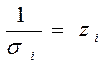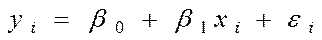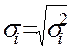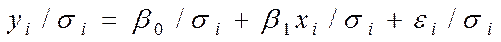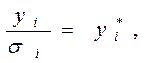
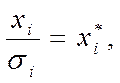
Для простоти викладу опишемо ВНК на прикладі парної регресії: Розділимо обидві частини (7.5) на , одержимо: (6) Поклавши рівним 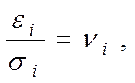одержимо рівняння регресії без вільного члена, але з додаткової пояснюючою змінної і з “перетвореним” відхиленням :

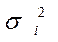
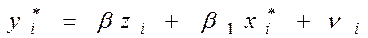Для застосування ВНК необхідно знати фактичні значення дисперсій відхилень. На практиці такі значення відомі вкрай рідко. Отже, щоб застосувати ВНК, необхідно зробити припущення про значення .

Наприклад, можна припустити, що дисперсії 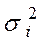відхилень 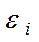пропорційні значенням 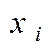(рис. 9) чи значенням 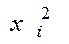(рис. 10).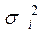

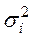
20. Методи усунення автокореляції. Авторегресійне перетворення.

Серед основних методів усунення автокореляції можна виділити:

1. Правильну специфікацію моделі (залучення значущих факторів або зміна форми залежності). Основною причиною наявності випадкової величини в узагальненій кореляційно-регресійній моделі є неможливість урахувати всі значущі фактори і взаємозв'язки,що зумовлюють певне значення результуючої змінної. Потрібно спробувати ідентифікувати факторну ознаку, яку не враховано в КРМ і врахувати її. Також можна спробувати змінити форму залежності( наприклад, лінійну на нелінійну).

2. Використання AR(1)-моделі (авторегресійної моделі Маркова 1-го порядку). Якщо віс доступні процедури зміни специфікації моделі вичерпані,а автокореляція наявна,то можна припустити, що вона обумовлена внутрішніми властивостями певних значень випадкових відхилень . У цьому разі можна скористатися авто регресійним перетворенням. У лінійній кореляційно-регресійній моделі або в моделях, що зводяться до лінійної, найдоцільнішим і простим перетворенням є авто регресійна модель Маркова першого порядку AR(1).

21. Методи усунення мультиколінеарності.

Розглянемо існуючі методи усунення мультиколінеарності:

1. Виключення змінної(их) з моделі. Цей метод полягає в тому, що високо корельовано пояснюючі змінні видаляються з регресії, та вона заново оцінюється. Відбір змінних, що підлягають виключенню, виконується за допомогою коефіцієнта кореляції. Для цього розраховується оцінка значимості коефіцієнтів парної кореляції rij між пояснюючими змінними xi та xj. Досвід свідчить, що якщо |rij|>0.85, то одну з змінних можна виключити. Але яку змінну видалити з аналізу, вирішують виходячи з економічних міркувань.

2. Покрокова регресія. В аналіз послідовно додається по одній пояснюючій змінній. На кожному кроці перевіряється значимість коефіцієнтів регресії та оцінюється мультиколінеарність змінних. Якщо оцінка коефіцієнта отримується не значимою, то змінна виключається та розглядають іншу пояснюючу змінну. Якщо оцінка коефіцієнта кореляції значима, а мулько лінеарність відсутня, то ця змінна залишається і в аналіз включають наступну змінну. Таким чином, поступово визначають всі змінні, що складають регресію без порушення передумови про відсутність мультиколінеарності.

3. Зміна специфікації моделі: або змінюється форма моделі, або додаються пояснюючі змінні, не враховані в первісній моделі, але істотно впливають на залежну змінну.

4. Використання попередньої інформації про деякі параметри. Зазвичай на основі раніше проведеного регресійного аналізу або в результаті економічних досліджень вже є більш або менш точне уявлення про величину або співвідношення двох або декількох коефіцієнтів регресії. Ця попередня або не вибіркова інформація може бути використана дослідником при побудові регресії. У зв’язку з тим.., що частина оцінок, отримана на основі не вибіркових даних, вже має достатньо чітку інтерпретацію. Це полегшує шлях знаходження взаємних впливів змін різних змінних.

5. Перетворення змінних. У ряді випадків мінімізувати або взагалі усунути проблему мультиколінеарності можна за допомогою перетворення змінних.

22. Моделі ANCOVA

Моделі, у яких пояснюючі змінні носять як кількісний, так і якісний характер, називаються ANСOVA – моделями.

Спочатку розглянемо найпростішу ANСOVA – модель з однією кількісною й однією якісною змінною, що та має два альтернативних стани:

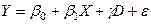(2)

Нехай, наприклад, 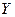– заробітна плата співробітника фірми, 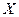– стаж співробітника, 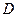– стать співробітника, тобто

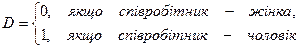
Тоді очікуване значення заробітної плати співробітників при 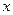роках виробничого стажу буде:

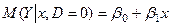– для жінки, (3)

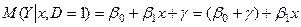– для чоловіка. (4)

Якщо якісна змінна має 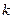альтернативних значень, то при моделюванні використовуються тільки 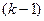фіктивних змінних. Якщо не застосовувати це правило, то при моделюванні дослідник попадає в ситуацію досконалої мультиколінеарності.

Значення фіктивної змінної можна змінювати на протилежні.

Значення якісної змінної, для якого приймається 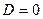, називається базовим. Вибір базового значення звичайно диктується цілями дослідження, але може бути і довільним.

Коефіцієнт 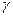у моделі (2) іноді називається диференціальним коефіцієнтом вільного члена, тому що він показує, на яку величину відрізняється вільний член моделі при значенні фіктивній змінної рівної одиниці, від вільного члена моделі при базовому значенні фіктивної змінної.

Нехай розглядається модель із двома пояснюючими змінними, одна з яких кількісна, а інша – якісна. Причому якісна змінна має три альтернативи. Наприклад, витрати на утримання дитини можуть бути зв'язані з доходами сімей і віком дитини: дошкільний, молодший шкільний і старший шкільний. Якісна змінна зв'язана з трьома альтернативами, тому за загальним правилом моделювання необхідно використовувати дві фіктивні змінні. Таким чином, модель може бути представлена у вигляді:

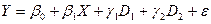(5)

де 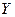– витрати, 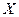– доходи сімей.

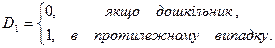
Утворяться наступні залежності. Середня витрата на дошкільника:

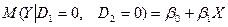(6)

Середні витрати на молодшого школяра:

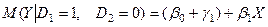(7)

Середні витрати на старшого школяра:

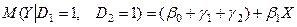(8)

де 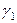, 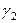– диференціальні вільні члени. Базовим значенням якісної змінної є значення “дошкільник”.

Після обчислення коефіцієнтів рівнянь регресії (6) – (8) визначається статистична значущість коефіцієнтів 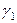і 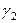на основі звичайної 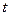-статистики.

Якщо коефіцієнти 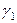і 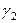виявляються статистично незначущими, то можна зробити висновок, що вік дитини не впливає на витрати по його утриманню.

23. Моделі ANOVA.

Дисперсійний аналіз ( ANOVA ) являє собою статистичний метод аналізу результатів, які залежать від якісних ознак.
Кожен фактор може бути дискретною чи неперервною випадковою змінною, яку розділяють на декілька сталих рівнів (градацій, інтервалів). Якщо кількість вимірювань (проб, даних) на всіх рівнях кожного з факторів однакова, то дисперсійний аналіз називають рівномірним, інакше -нерівномірним.
В основі дисперсійного аналізу є такий принцип (факт з математичної статистики): якщо на випадкову величину діють взаємно незалежні фактори A, B, …, то загальна дисперсія дорівнює сумі дисперсій, зумовлених дією окремо кожного з факторів:
{\displaystyle \sigma ^{2}=\sigma _{A}^{2}+\sigma _{B}^{2}+\ldots }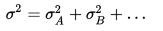

Дисперсійний аналіз полягає у виділенні й оцінюванні окремих факторів, що викликають зміну досліджуваної випадкової величини. При цьому проводиться розклад сумарної вибіркової дисперсії на складові, обумовлені незалежними факторами. Кожна з цих складових є оцінкою дисперсії генеральної сукупності. Щоб дати оцінку дієвості впливу даного фактору, необхідно оцінити значимість відповідної вибіркової дисперсії у порівнянні з дисперсією відтворення, обумовленою випадковими факторами. Перевірка значимості оцінок дисперсії проводять з допомогою критерію Фішера.
Коли розрахункове значення критерію Фішера виявиться меншим табличного, то вплив досліджуваного фактору немає підстав вважати значимим. Коли ж розрахункове значення критерію Фішера виявиться більшим табличного, то цей фактор впливає на зміни середніх. В подальшому ми вважаємо, що виконуються наступні припущення:

1. Випадкові помилки спостережень мають нормальний розподіл.

2. Фактори впливають тільки на зміну середніх значень, а дисперсія спостережень залишається постійною.

Фактори, що розглядаються в дисперсійному аналізі, бувають трьох родів:

· з випадковими рівнями, коли вибір рівнів проходить з безмежної сукупності можливих рівнів та супроводжується рандомізацією і рівні вибираються випадковим чином;

· з фіксованими рівнями;

· змішаного типу — частина факторів розглядається на фіксованих рівнях, але рівні решти вибираються випадковим чином.

24. Наведіть формули для розрахунків коефіцієнтів емпіричного парного лінійного рівняння регресії за МНК.

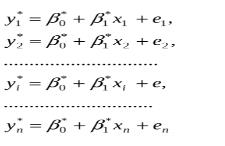
25. Нелінійні моделі та їх лінеаризація. Приклади використання в економіці.

Найбільш популярною моделлю в економіці є лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовуються складніші моделі з нелінійною залежністю між показником у та фактором х. За методикою оцінок параметрів парні нелінійні регресії розглядаються двох видів: 1) нелінійні за факторами, але лінійні за невідомими параметрами, які підлягають оцінці; 2) нелінійні за факторами і параметрами. Регресії, нелінійні за факторами, але лінійні за оцінюваними параметрами, називаються квазілінійними.
Парну квазілінійну регресію можна записати в загальному вигляді: 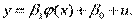Заміною величин 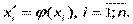нелінійна парна регресія приводиться до лінійної парної регресії: 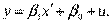Формули для оцінок параметрів набувають вигляду

,

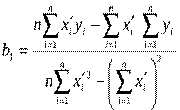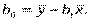
Коефіцієнт еластичності для парної квазілінійної регресії оцінюється за формулою 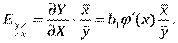Для оцінки коефіцієнта еластичності нелінійної регресії в загальному використовується формула: 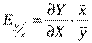, де 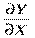- частинна похідна функції у за змінною х.
В регресіях нелінійних за факторами та параметрами логарифмують праву та ліву частину рівняння і проводять заміну змінних. Таким чином нелінійна регресія зводиться до лінійного виду. Параметри лінійної моделі оцінюють за відомими формулами використовуючи в якості вихідних даних значення нових змінних. Для оцінки адекватності нелінійної парної регресії спостережуваним даним можна використовувати критерій Фішера. Перевірка виконується за таким же алгоритмом, що й для лінійної парної регресії.
Довірчі межі прогнозу для квазілінійної парної регресії оцінюються за тими ж формулами, що й для лінійної парної регресії, лише замість х розглядають х^/ . Інтервальний прогноз індивідуального значення при заданому рівні значимості α = 0,05 для y_n+1 знаходять за формулою:

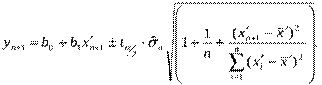
Інтервал довіри для математичного сподівання y_n+1 :

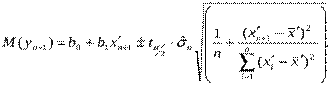
У тих випадках, коли нелінійна регресія перетворюється в лінійну шляхом логарифмування і заміни змінних, довірча інтервальний прогноз знаходять для відповідної лінійної регресії, а потім, використовуючи зворотні перетворення для меж інтервалів довіри прогнозу лінійної регресії, знаходять межі інтервалів довіри прогнозу нелінійної регресії.

26. Об'єкт, предмет та мета економетрії. Основне завдання економетричних досліджень.

Об'єктом економетрії є економічні системи та простори різного рівня складності: від окремого підприємства чи фірми до економіки галузей, регіонів, держави й світу загалом.

Предмет економетрії — це методи побудови та дослідження математико-статистичних моделей економіки, проведення кількісних досліджень економічних явищ, пояснення та прогнозування розвитку економічних процесів.

Метою економетричного дослідження є аналіз реальних економічних систем і процесів, що в них відбуваються, за допомогою економетричних методів і моделей, їх застосування при прийнятті науково обґрунтованих управлінських рішень.

Основне завдання економетрії — оцінити параметри моделей з урахуванням особливостей вхідної економічної інформації, перевірити відповідність моделей досліджуваному явищу і спрогнозувати розвиток економічних процесів.

27. Опишіть процес перевірки адекватності моделі за F-критерієм Фішера.

Коефіцієнт детермінації:

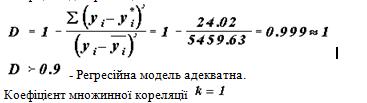
Розрахувати і побудувати графік рівняння прямолінійної регресії для відносних значень PWC170 і часу човникового бігу 3х10 м у 13 досліджуваних і зробити висновок про точність розрахунку рівнянь, якщо дані вибірок такі:
xi, кГ м / хв / кг ~ 15,6; 13,4; 17,9; 12,8; 10,7; 15,7; 11,7; 12,3; 12,3; 11,1; 14 , 3; 12,7; 14,4 yi, з ~ 6,9; 7,2; 7,1; 6,7; 7,6; 7,0; 6,4; 6,9; 7,7; 7,6; 7,9; 8,2; 6,8
Рішення
1. Занести дані тестування в робочу таблицю і зробити відповідні розрахунки.

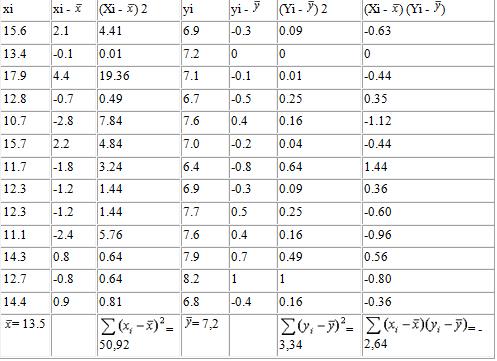
1. Розрахувати значення нормованого коефіцієнта кореляції за формулою:

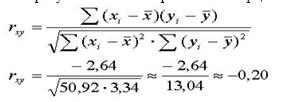
3. Розрахувати кінцевий вигляд рівнянь прямолінійної регресії за формулами (2) і (3):

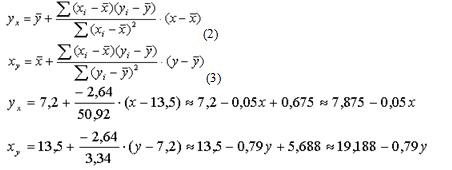
Тобто

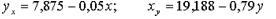
4. Розрахувати абсолютні похибки рівнянь регресії за формулами (4) і (5):

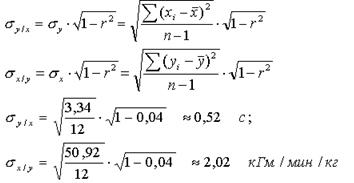
5. Розрахувати відносні похибки рівнянь регресії за формулами (6) і (7):

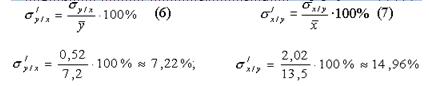
6. Для графічного подання кореляційної залежності між ознаками розрахувати координати ліній регресії, підставивши в кінцевий вигляд рівнянь (1) і (2) дані будь-якого досліджуваного (наприклад, четвертого зі списку).
Тоді:
при х = 12,8 кгм / хв / кг у = 7,235 с »7,2 з;
при у = 6,7 с х = 13,895 с »13,9 кгм / хв / кг.
7. Уявити графічно дане рівняння регресії.

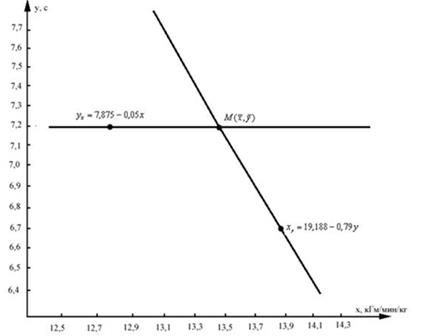
8. На підставі проведених розрахунків і графічного зображення рівняння регресії зробити висновок.

28. Опишіть процес перевірки статистичної значущості коефіцієнта кореляції за допомогою t-теста Стьюдента

Для перевірки статистичної значущості коефіцієнта кореляції за t-критерієм Стьюдента необхідно:

1) розрахувати t-відношення: 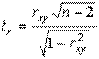; (3)

2) з таблиць критичних точок розподілу Стьюдента знайти 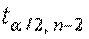, де a – рівень значущості, зв’язаний з рівнем надійності P співвідношенням: a = 1 - P ;

3) якщо 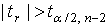коефіцієнт r_xy статистично значимо відрізняється від нуля.

29. Оцінка дисперсії залишків та дисперсій коефіцієнтів парної регресії.

· Дисперсія залишків ( випадкова дисперсія) D_u = 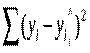характеризує міру відхилень значень залежного фактораy_i від розрахованихзначень за моделлю y_i^.

Оцінка дисперсії залишків здійснюється за форм улою: S² = SSE/(n - k) .

30. Оцінка моделей з лаговими змінними. Метод послідовного збільшення кількості лагів.

За даним методом рівняння y_t = a + b₀×x_t +b₁×x_t-1 …+ b_k×x_t-k +…+ e_t рекомендується оцінювати з послідовно збільшенням кількості лагів. Ознак завершення процедури збільшення кількості лагів може бути кілька.

• При додаванні нового лага який-небудь коефіцієнт регресії bkпри змінної xt-кменяет знак. Тоді в рівнянні регресії залишають змінні xt, xt-1, .... xt-k+1коэффициенты при яких знак не поміняли.

• При додаванні нового лага коефіцієнт bkрегрессии при змінній Xt-кстановится статистично незначущу.

Очевидно, що в рівнянні будуть використовуватися тільки змінні xt, xt-1, .... xt-k+1коэффициенты при яких залишаються статистично значущими.

Однак застосування цього методу досить обмежена в силу постійно зменшується числа ступенів свободи, що супроводжується збільшенням стандартних помилок та погіршенням якості оцінок, а також можливості мультиколінеарності. Крім цього, при неправильному визначенні кількості лагів можливі помилки специфікації.