6 Лабораторная работа. Измерение индуктивности и емкости в цепи переменного тока

Дата: 2025-06-02; Просмотры: 16
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Цель работы: изучение цепей переменного тока с активным, емкостным и индуктивным сопротивлением.

 

6.1 Теоретические сведения

 

Рассмотрим электрические колебания, возникающие в цепи, где имеется генератор, электродвижущая сила которого изменяется периодически. Они подобны вынужденным периодическим колебаниям тела, которые вызываются периодической внешней силой.

Мы ограничимся только цепями с сосредоточенными емкостями и индуктивностями и будем считать переменные токи квазистационарными. Иными словами, мы будем предполагать, что промежуток времени τ, в течение которого электрические величины принимают установившиеся значения, мал по сравнению с периодом колебаний 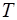, и поэтому будем применять к мгновенным значениям всех электрических величин законы постоянного тока.

Далее, мы будем рассматривать только такие токи, мгновенные значения которых 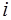изменяются во времени 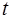по гармоническому закону (синусоидальному или косинусоидальному):

 

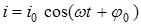, (6.1)

где 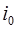– амплитуда силы тока,

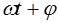0–фаза колебаний,

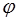0–начальная фаза,

ω–циклическая частота, связанная с периодом колебаний .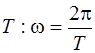

Это объясняется несколькими причинами. Во–первых, все технические генераторы переменного тока имеют э.д.с., изменяющуюся по закону, очень близкому к гармоническому, и потому создаваемые ими токи практически являются синусоидальными. Вторая причина заключается в том, что теория синусоидальных токов проста, и поэтому на примере таких токов можно выяснить основные особенности электрических колебаний.

Наконец, везде в дальнейшем мы будем считать, что колебания являются установившимися. Иными словами, будем предполагать, что с момента начала колебаний прошло достаточно большое время, так что амплитуды тока и напряжения уже достигли постоянного значения.

 

6.2 Активное сопротивление в цепи переменного тока

 

Рассмотрим сначала частный случай, когда генератор переменного тока замкнут на внешнюю цепь, имеющую сопротивление R и настолько малые индуктивность и емкость, что ими можно пренебречь. Сопротивление резистора называется активным, так как оно обуславливает необратимый переход электрической энергии во внутреннюю энергию проводника, который при этом нагревается. Положим, что в цепи идет переменный ток

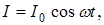(6.2)

и найдем, по какому закону изменяется напряжение между концами внешней цепи (рисунок 6.1).

     

 

 

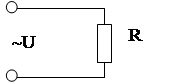Рисунок 6.1 Рисунок 6.2

Применяя закон Ома, имеем

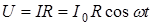. (6.3)

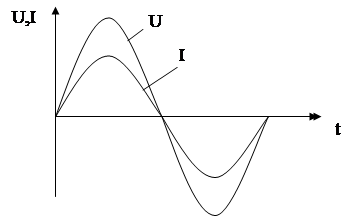
Таким образом, напряжение на концах участка цепи изменяется также по гармоническому закону, причем разность фаз между колебаниями тока и напряжения равна нулю. Это означает, что напряжение и ток одновременно достигают максимальных значений, одновременно обращаются в нуль и т. д. (рисунок 6.2). Максимальное значение напряжения 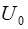равно произведению амплитуды силы тока на активное сопротивление 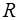участка цепи .

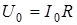Гармонически изменяющиеся величины можно наглядно изображать при помощи векторных диаграмм.

Выберем ось диаграммы таким образом, чтобы вектор, изображающий колебания тока, был направлен вдоль этой оси. В дальнейшем мы будем называть его осью токов. Вектор, изображающий колебания напряжения, будет направлен вдоль оси токов (рисунок 6.3). Поскольку разность фаз между током и напряжением равна нулю, то длина этого вектора равна амплитуде напряжения .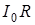

 

 

 

Рисунок 6.3

 

6.3 Емкость в цепи переменного тока

 

Положим теперь, что участок цепи содержит конденсатор емкости 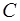, причем сопротивлением и индуктивностью можно пренебречь. Выясним, по какому закону будет изменяться напряжение на концах участка цепи в этом случае. Полагаем, что сила тока изменяется по закону .

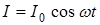Напряжение на конденсаторе равно

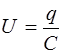. (6.4)

Ток можно записать через величину заряда 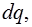протекающего через сечение проводника и увеличивающего заряд конденсатора за промежуток времени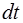

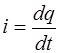. (6.5)

Тогда заряд конденсатора можно найти интегрированием

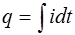. (6.6)

Поскольку сила тока в цепи изменяется по закону

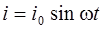, (6.7)

то заряд равен

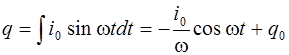. (6.8)

Постоянная интегрирования 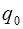здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим 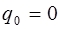. Следовательно, с учетом формулы (6.4) можно записать для напряжения

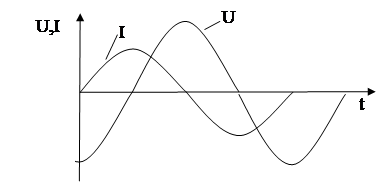
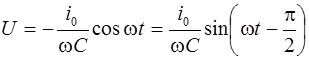(6.9)

 

 

 

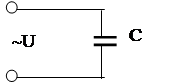Рисунок 6.4 Рисунок 6.5

Сравнение выражений (6.7) и (6.9) показывает, что при гармонических колебаниях тока в цепи напряжение на конденсаторе изменяется также по гармоническому закону, однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на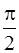

Изменение тока и напряжения во времени изображено графически на рисунке 6.5.

Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой – либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому колебания напряжения, как и колебания заряда, запаздывают относительно колебаний тока. Так, например, когда в момент времени 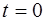сила тока равна нулю (рисунок 6.5), то на пластинах конденсатора еще имеется заряд, перенесенный током в предыдущий промежуток времени, и напряжение не равно нулю. Для обращения в нуль этого заряда нужно, чтобы в течение промежутка времени, равного 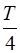, проходил ток положительного направления. Однако, когда заряд конденсатора (а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю (рисунок 6.5)–она принимает максимальное значение.

Формула (6.9) показывает, что амплитуда напряжения на конденсаторе равна

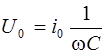. (6.10)

Сравнивая это выражение с законом Ома для участка цепи постоянного тока 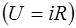, мы видим, что величина

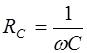, (6.11)

зависящая от емкости конденсатора 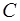, играет роль сопротивления участка цепи. Поэтому она получила название кажушегося сопротивления емкости или емкостным сопротивлением. Емкостное сопротивление равно отношению амплитуды напряжения на емкости к амплитуде силы тока в цепи. В Международной системе единиц СИ емкостное сопротивление выражается в омах. 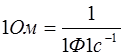. Емкостное сопротивление равно величине, обратной произведению электрической емкости ( в 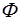) и циклической частоты переменного тока 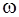(в ).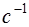

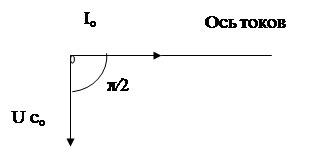Полученные результаты можно представить в виде векторной диаграммы (рисунок 6.6). Здесь вектор, изображающий колебания напряжения, уже не совпадает с осью токов. Он повернут в отрицательном направлении (по часовой стрелке) на угол 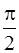. Модуль этого вектора равен амплитуде напряжения .

 

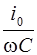Рисунок 6.6

Из формулы (6.11) видно, что сопротивление емкости 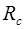зависит также от частоты 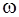. Поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока.

 

6.3 Индуктивность в цепи переменного тока

 

Рассмотрим, наконец, третий частный случай, когда участок цепи содержит только индуктивность. (рисунок 6.7).

 

 

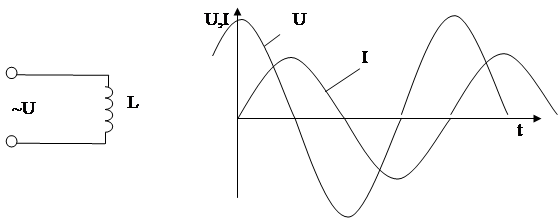Рисунок 6.7 Рисунок 6.8

При наличии переменного тока в катушке индуктивности возникнет э.д.с. самоиндукции, и поэтому мы должны применить закон Ома для участка цепи с э.д.с.

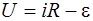. (6.12)

В нашем случае R=0, а э.д.с. самоиндукции

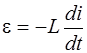. (6.13)

Поэтому

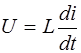. (6.14)

Если сила тока в цепи изменяется по закону

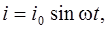(6.15)

то 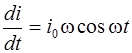, и тогда напряжение

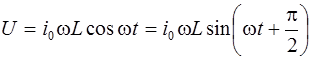. (6.16)

Из сравнения выражений (62) и (63) видно, что колебания напряжения на индуктивности опережают по фазе колебания тока на 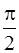. Когда сила тока, возрастая, проходит через нуль, напряжение уже достигает максимума, после чего начинает уменьшаться; когда сила тока становится максимальной, напряжение проходит через нуль, и т.д. (рисунок 6.8).

Физическая причина возникновения этой разности фаз заключается в следующем. Если активное сопротивление катушки индуктивности равно нулю, то приложенное напряжение в точности уравновешивает э.д.с. самоиндукции и поэтому равно э.д.с. самоиндукции с обратным знаком. Но э.д.с. пропорциональна не мгновенному значению тока, а быстроте его изменения, которая будет наибольшей в те моменты, когда сила тока проходит через нуль. Поэтому максимумы напряжения совпадают с нулями тока и наоборот.

Из (6.16) следует, что амплитуда напряжения равна

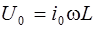, (6.17)

и, следовательно, величина

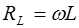, (6.18)

играет ту же роль, что и сопротивление участка цепи. Поэтому 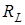называют кажущимся сопротивлением индуктивности или индуктивным сопротивлением. Индуктивное сопротивление равно отношению амплитуды ЭДС самоиндукции к амплитуде силы тока в цепи. В СИ индуктивное сопротивление выражается в Омах. Индуктивное сопротивление равно произведению индуктивности 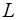(в Гц) и циклической частоты тока 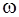(в с-1).

Так как полученные результаты можно представить с помощью векторной диаграммы. Она показана на рисунке 6.9. Вектор, изображающий колебания напряжения, повернут относительно оси токов в положительном направлении (против часовой стрелки) на угол 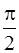, а его модуль, равный амплитуде напряжения, есть UL0=i0RL

 

 

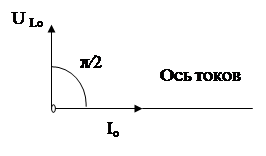Рисунок 6.9

 

 

6.4 Закон Ома для цепи переменного тока

 

Реальные цепи переменного тока, как правило, содержат все виды сопротивлений, включенных как последовательно, так и параллельно. Рассмотрим цепь из последовательного соединения резистора R, катушки 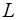и конденсатора С (рисунок 6.10).

 

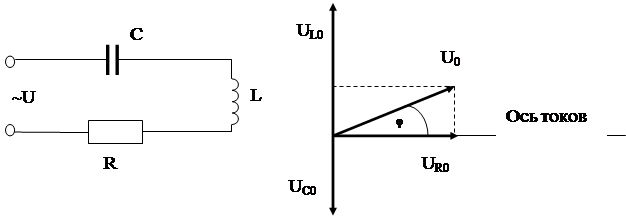
Рисунок 6.10 Рисунок 6.11

 

Положим по–прежнему, что ток в цепи изменяется по закону

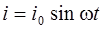, (6.19)

и вычислим напряжение между концами цепи. Так как при последовательном соединении проводников складываются напряжения, то искомое напряжение есть сумма трех напряжений: на сопротивлении, на емкости и на индуктивности, причем каждое из этих напряжений, как следует из выражений (6.3), (6.9) и (6.16), изменяется во времени по закону синуса.

Для сложения этих трех гармонических колебаний мы воспользуемся векторной диаграммой напряжения (рисунок 6.11). Колебания напряжения на активном сопротивлении изображаются вектором UR0, направленным вдоль оси токов и имеющим модуль UR0=i0R; колебания напряжения на индуктивности и емкости – векторами, перпендикулярными к оси токов, c модулям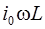и и .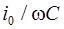

На векторной диаграмме результирующее направление изображается векторной суммой трех векторов, причем длина результирующего вектора равна амплитуде напряжения 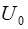, а угол, образованный результирующим вектором с осью токов,—сдвигу фазы 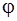. Из треугольника напряжений (рисунок 6.11) получаем

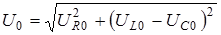(6.20)

Или:

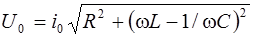. (6.21)

Напряжение в цепи изменяется по закону:

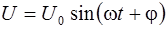. (6.22)

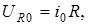
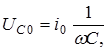
Поскольку 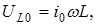то можно построить аналогично диаграмме напряжений (рисунок 6.11) диаграмму сопротивлений (рисунок 6.12). Из рисунка 6.12 видно, что

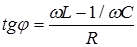. (6.23)

 

 

 

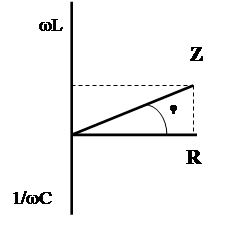Рисунок 6.12

Формула (6.21) имеет сходство с законом Ома в том смысле, что амплитуда напряжения 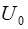пропорциональна амплитуде тока 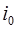. Поэтому выражение (6.21) иногда называют законом Ома для переменного тока. Однако нужно помнить, что эта формула относится только к амплитудам, но не к мгновенным значениям 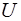и .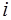

В случае постоянного тока отношение напряжения к силе тока называют сопротивлением проводника. Подобно этому при переменном токе отношение амплитуды полного напряжения к амплитуде тока

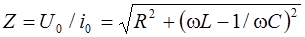(6.24)

называют сопротивлением цепи для переменного тока.

Аналогично отношение амплитуды активной составляющей напряжения 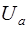к амплитуде тока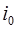

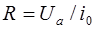(6.25)

называется активным сопротивлением цепи. В рассмотренной цепи оно равно сопротивлению для постоянного тока. Активное сопротивление всегда приводит к выделению тепла Джоуля—Ленца.

Выражение

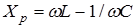(6.26)

есть реактивное сопротивление цепи. Для данного случая оно равно разности кажущихся сопротивлений индуктивности и емкости. Наличие реактивного сопротивления не сопровождается выделением тепла. Из формулы (6.24) видно, что активное и реактивное сопротивления цепи складываются геометрически.

Большинство электроизмерительных приборов измеряют не амплитудные, а эффективные значения напряжений и токов, имеющие следующую связь с амплитудными:

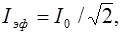
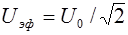. (6.27)

 

6.5 Приборы и принадлежности: катушка индуктивности, конденсатор, регулятор напряжения, вольтметр, амперметр, соединительные провода.

 

6.6 Порядок выполнения работы

 

1. Соберите схему по рисунку 6.13.

 

 

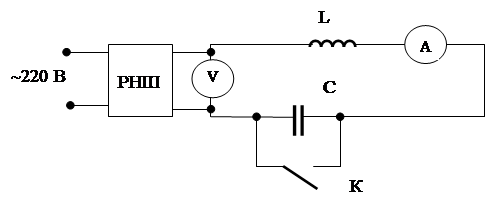Рисунок 6.13.

2. Замкните ключ К и, подав в цепь напряжение U, измерьте силу тока I1.

3. Разомкните ключ К и измерьте силу тока I2.

4. Измерьте активное сопротивление катушки R.

5. Повторите измерения три раза при разных значениях напряжения. Результаты занесите в таблицу 6.1.

6. Вычислите:

· Индуктивное сопротивление цепи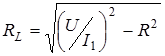

· индуктивность катушки 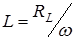, ( 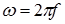=314 с-1.)

· емкостное сопротивление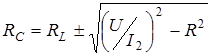

· емкость конденсатора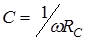

7. Постройте в масштабе векторную диаграмму для действующих значений напряжений ,вычислив их для наибольшего значения силы тока I2:

, , .

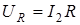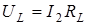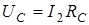Таблица 6.1

U,В I1,А I2,А R,Ом RL,Ом L,Гн <L>,Гн RC,Ом C,Ф <C>,Ф
                   

 

6.7 Контрольные вопросы

 

1. Что называется активным сопротивлением цепи? Что называется индуктивным сопротивлением цепи?

2. Выведите формулу для нахождения индуктивного сопротивления цепи.

3. Дайте определение емкостного сопротивления цепи переменного тока.

4. Выведите формулу для нахождения емкостного сопротивления цепи.

5. Постройте векторные диаграммы токов и напряжений для цепей переменного тока, содержащих различные элементы.

6. Выведите формулу полного сопротивления последовательно соединенных резистора, катушки и конденсатора.

 

6.8 Техника безопасности

 

1. Включать установку разрешается только после проверки преподавателя или инженера.

2. Во избежание электротравмы не касайтесь руками металлических частей схемы.

3. Разбирать схему можно, только отключив источник питания.