Лабораторная работа № 4
«Структура цикл»
1. Цель выполнения работы
Изучить и сравнить особенности построения алгоритмов и разработки программ алгоритмических структур «Цикл» и «Цикл в цикле»: «Итерационные циклы», «Циклы с параметром», «Цикл с предусловием», «Цикл с постусловием».
2. Основные сведения из теории
Для выполнения лабораторной работы и ответа на контрольные вопросы рекомендуется использовать конспект лекций и электронный учебник.
3. Порядок выполнения работы
В каждом варианте задания необходимо выполнить постановку задачи, определить требуемые входные и выходные данные для решения предложенных задач. Разработать математические модели, схемы алгоритмов и программы. Предусмотреть печать входных и выходных данных в виде таблицы с шапкой. Начальные и конечные значения параметров циклов и величины шага их изменения задать в качестве входных данных. В двух заданиях реализовать алгоритм цикла с предусловием и с постусловием. В программах использовать три оператора цикла. Вручную просчитать контрольные примеры для, выбранных самостоятельно, значений параметров цикла. Отладить программы и оформить отчет.
4. Варианты задания
Вариант 1
1. Железнодорожный состав проходит первую треть пути со скоростью V1, а оставшуюся часть пути - со скоростью V2. Определить скорость на первом участке пути по формуле:

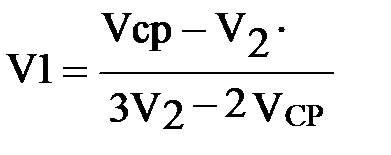 ,
,
если V2=50 км/ч, а средняя скорость поезда на всем пути
Vср=37,5 км/ч, 40 км/ч, 45 км/ч, 62 ,5 км/ч, 74 км/ч.
2. Определить ускорение скатывающегося с горки вагона с учетом инерции его вращающихся частей:
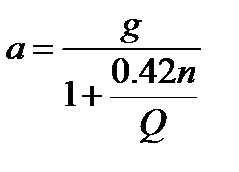
где g = 9,81м/c2;
число осей вагона n = 4, 6, 8;
вес вагона Q = 40, 60, 80, ...., 140 т.
Вариант 2
1. Двигаясь с ускорением a, поезд достигает скорости Vt=60 км/ч.
За какое время эта скорость достигнута и какой путь пройден за это время?
Искомые величины получить для всех а, принимающих значения от 0,4 м/c2 до 1,0 м/c2 c шагом 0,1 м/c2
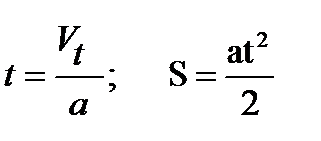 ;
;
2. Определить зависимость фокусного расстояния стеклянной линзы от радиусов ее сферических поверхностей, если показатель преломления стекла m=1,5;
F = 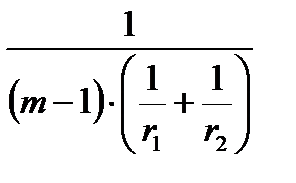
где 4,2 £ r1 £ 12,2 c шагом 2 см,
6,4 £ r2 £ 24,4 c шагом 2 см. 
Вариант 3
1. За i-ю секунду от начала движения поезд прошел L метров. Какой путь пройдет поезд за первые t секунд и какой скорости он достигнет по истечении этого времени?
St=at2 Vt=at a= 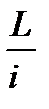 (м/с2)
(м/с2)
Отладку программы произвести для значений i=4, t=10, 3 ≤ L ≤ 9 c шагом 0,5 м.
2. Груз массой m перемещают равномерно по прямой в горизонтальной плоскости, прилагая силу, направленную под углом 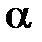 к горизонту. Определить величину этой силы при изменяющихся значениях угла
к горизонту. Определить величину этой силы при изменяющихся значениях угла 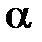 и коэффициента трения
и коэффициента трения 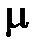
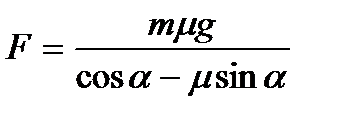 ,
,
где 0 £ α £ 0,5 рад с шагом 0,1 рад ; 0,1£ m £ 0,2 с шагом 0,02; m=10кг.
Вариант 4
1. Найти скорость поезда , при которой маятник длинной r , подвешенный в вагоне, раскачивается особенно сильно ,если длина рельсов L=12,5 м ; g=9,81 м/c2
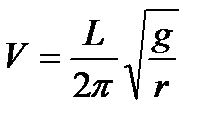 ,
,
40 £ r £ 80 cм с шагом 4 см
2. Вычислить значения функции a = (bx + cy)* sin(xy)
при изменении x в пределах от 1 до 2 c шагом 0,25 и y в пределах
от 4,2 до 5,1 c шагом 0,3.
Вариант 5
1. Участок пути длиной S=1,0 км локомотив проходит с постоянным ускорением а. За какое время этот путь прйден и какова скорость в конце данного участка пути, если 0,2 £ a £ 1,2 м/c2 с шагом 0,2 м/c2 ?
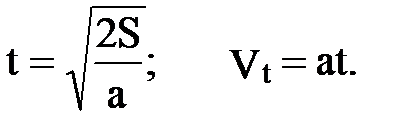
2. Вычислить расстояние между неподвижной и движущейся точками в косоугольной системе координат по формуле:
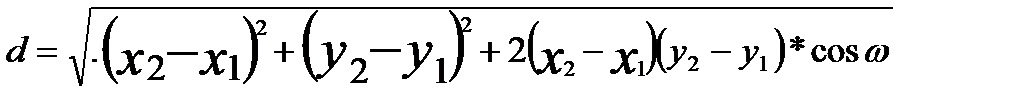 ,
,
где х1=0; y 2=0; 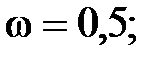 1 £ x2 £2 с шагом 0,25;
1 £ x2 £2 с шагом 0,25;
1,5£ y2 £ 6,0 с шагом 0,75;
Вариант 6
1. Поезд массой m трогается с места и двигается по горизонтальному пути под действием постоянной силы тяги локомотива F . Коэффициент сопротивления движению k. Определить ускорение поезда и скорость, достигнутую им через t секунд после начала движения, если
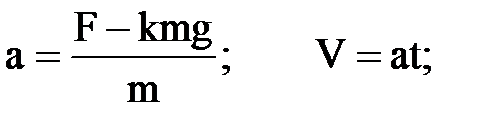
причем F=4000 H; k=0,005; t=5 c; g=9,81 м/c2;
2000 £ m £ 4000 т. с шагом 250 т.
2. Вычислить значение функции :
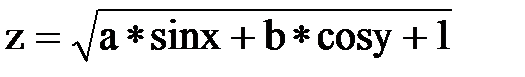 ;
;
при изменении аргументов в интервалах 0 ≤ x ≤ 2,4 c шагом 0,4 и
1,0 ≤ y ≤ 2,0 c шагом 0,1; a = 2,97; b = 4,56.
Вариант 7
1.Поезд массой m , движущийся со скоростью V, остановился, пройдя после торможения путь S. Определить, как изменяется величина тормозной силы и время торможения в зависимости от скорости
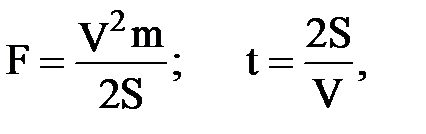
где m=2000т ; S=550м ; 30 £ V£ 60 c шагом 5 км/ч.
2. Вычислить и напечатать таблицу значений функций
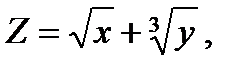

где 1,5 £ x £ 12,0 с шагом 3,5
12 £ y £ 16 c шагом 2.
Вариант 8
1. Как изменяется центростремительное ускорение поезда, движущегося по закруглению дороги со скоростью V, в зависимости от радиуса r ? 

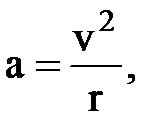
где V=60 км/ч ; 200 £ r £ 1000 м с шагом 100 м.
2. Определить статический и динамический прогибы балки по формулам
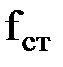 =
= 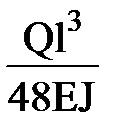 ; fg= fст +
; fg= fст + 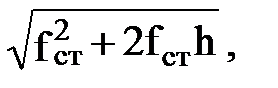

где E = 2×106 кг/см2 ; J=2500 cм4 ; Q = 4 т;
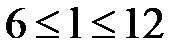 м с шагом 3 м;
м с шагом 3 м;
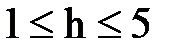 м с шагом 1м.
м с шагом 1м.
Вариант 9
1. Поезд, двигаясь под уклон, прошел за t секунд путь S и развил скорость V. Как изменяется ускорение поезда и какова была его скорость в начале уклона в зависимости от времени t ?
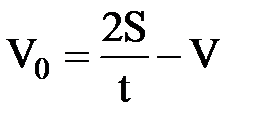 ;
; 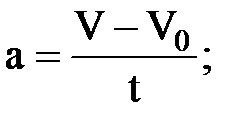

где S=340м ; V =19м/c ; 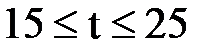 с шагом 1с.
с шагом 1с.
2.Объем усеченной пирамиды вычисляется по формуле
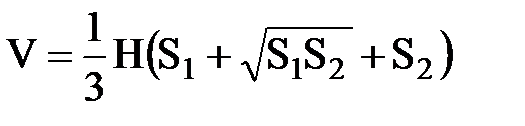 ,
,
где S1 и S2 – площади оснований ; H - высота.
Напечатать таблицу для следующих значений переменных:
S1= 0,5м ; 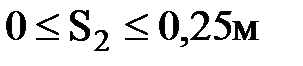 с шагом 0,05 м ;
с шагом 0,05 м ; 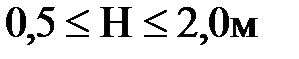 с шагом 0,5 м.
с шагом 0,5 м.
Вариант 10
1. Расстояние между двумя станциями поезд прошел со средней скоростью Vcр за t минут. Разгон и торможение вместе длились t1 минут, а остальное время поезд двигался равномерно. Определить скорость V равномерного движения при заданных значениях времени t1 .
. 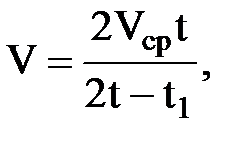
где Vср=72 км/ч ; t=20 мин; 2,5 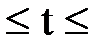 6,5 мин с шагом 30 сек.
6,5 мин с шагом 30 сек.
2. Расписание поездов освещается двумя источниками света силой I1 и I2 c расстояний X1 и X2 , Расстояние между источниками l .Определить изменение освещенности расписания в средней точке между источниками при изменении величин X1 и l.
 E=
E= 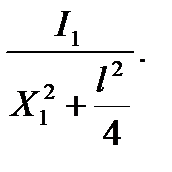
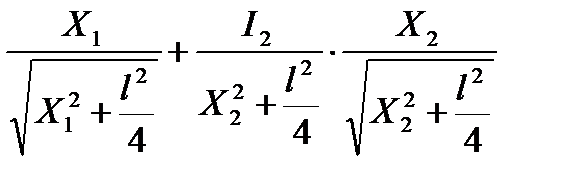 ,
,
где I1=150 кд ; I2=200 кд ; X2=1,5м ;
0,5 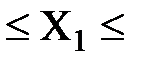 2 м с шагом 0,5 м ;
2 м с шагом 0,5 м ;
4 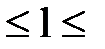 6 м c шагом 1 м.
6 м c шагом 1 м.
Вариант 11
1. Электровоз трогает с места состав массой m. С каким ускорением движется поезд в зависимости от массы, если коэффициент сопротивления m= 0,005, а сила тяги Fт=400 кН, g = 9.8 м/c2?
а = 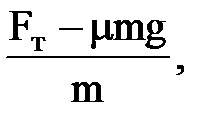
где 1500 ≤ m ≤ 2000 т с шагом 50 т.
2. Маятник длины l подвешен к потолку вагона, движущегося горизонтально по прямой с ускорением a. Как зависит положение равновесия и период колебаний маятника от его длины и ускорения вагона?
 a=arctg
a=arctg 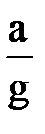 ; Т =
; Т = 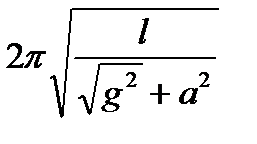
Отладить программу для следующих значений исходных данных:
g =9,8 м/c2; 0,75 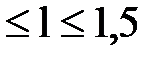 м с шагом 25;
м с шагом 25;
2,2 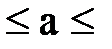 2,6 м/с2 с шагом 0,1м/с2.
2,6 м/с2 с шагом 0,1м/с2.
Вариант 12
1. Электропоезд в момент выключения тока имел скорость V. Какое время и расстояние пройдет он до полной остановки по горизонтальному пути при разных значениях скорости? Коэффициент сопротивления движению m.
t= 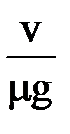 ; l=
; l= 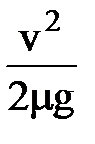 ,
,
где m= 0,006; g= 9,81 м/с2; 5 ≤ V ≤ 10 м/с с шагом 0,5 м/с.
2. Определить значения диаметра d оси железнодорожного вагона, представляющей балку с двум консолями, нагруженную силами P на концах консолей. Длина опорной части l = 1520 мм; длина консолей
a = 260 мм; допускаемое напряжение на изгиб R меняется от 500 до 600 кг/см2 с шагом 50 кг/см2; 5,0 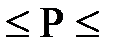 6,5 т с шагом 0,25 т
6,5 т с шагом 0,25 т
d= 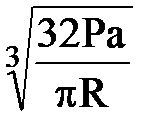 .
.
Результаты решения представить в виде таблицы.
Вариант 13
1. Вагон массой m подходит к неподвижной платформе со скоростью V1 и ударяет ее, после чего платформа получает скорость V. Скорость вагона после удара уменьшилась до V2. Вычислить значение массы платформы для ряда значений V: 0,1 ≤ V ≤ 1,5 м/с с шагом 0,25 м/с
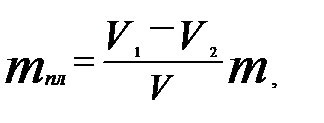
где m = 60 т; V1=0,2 м/с ; V2=0,1 м/c.
2. Найти расстояние между двумя точками на плоскости, положение которых задано их координатами X1,Y1 и X2,Y2 по формуле:
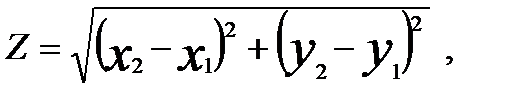
если -2 ≤ X 1 ≤ 2 с шагом 1; y1=2,5
- 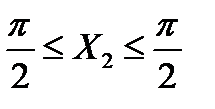 с шагом
с шагом 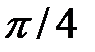 ; y2=sin2x2.
; y2=sin2x2.
Вариант 14
1. Какой массы состав может везти тепловоз с ускорением а при различных коэффициентах сопротивления 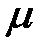 , если он развивает максимальное тяговое усилие FТ ?
, если он развивает максимальное тяговое усилие FТ ?
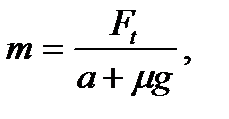
где а=0,1 м/c2; Ft=300 кН ; g=9,8 м/c2;
0,001 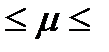 0,01 с шагом 0,001.
0,01 с шагом 0,001.
2. Колебательный контур состоит из конденсатора С и катушки с индуктивностью L и активным сопротивлением R=200 ом. Определить частоту свободных электромагнитных колебаний в этом контуре. На сколько изменится частота, если пренебречь активным сопротивлением катушки ?
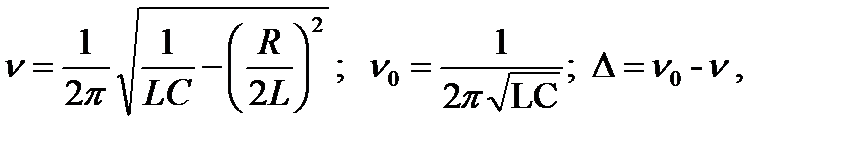
где 12∙10-3 £ L £ 24∙10-3 г с шагом 2∙10-3 г ;
48 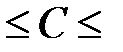 72 мкф с шагом 12 мкф.
72 мкф с шагом 12 мкф.
Вариант 15
1.Сколько вагонов может везти электровоз в гору с уклоном L , если коэффициент максимального трения покоя равен k2 ; коэффициент трения качения k1. Вес электровоза в 4 раза больше вагона.
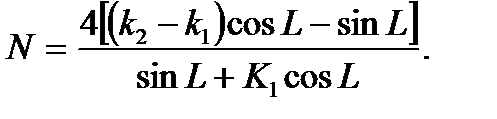
Проанализировать изменение функции для значений 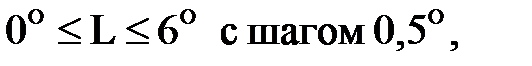
если k1=0,001; k2=0,1.
2.Напечатать таблицу объема шарового сегмента
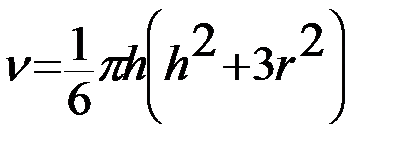
для следующих данных: 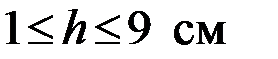 с шагом 1 см
с шагом 1 см
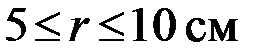 с шагом 2,5 см
с шагом 2,5 см
Вариант 16
1.Скорость истечения груза из горизонтального отверстия бункера равна:
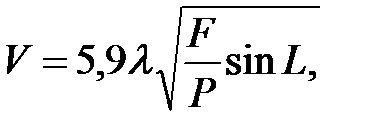
где 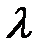 -коэффициент истечения ;
-коэффициент истечения ;
F-площадь поперечного сечения потока ;
Р-периметр сечения ;
L-угол наклона желоба , отклоняющего поток и создающего подпор.
Отладить программу для значения : 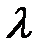 =0,6 ; F=0,36 м2 ; P=2,4 м2 ;
=0,6 ; F=0,36 м2 ; P=2,4 м2 ; 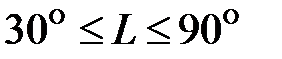 с шагом 100. Результаты напечатать в виде таблицы.
с шагом 100. Результаты напечатать в виде таблицы.
2.Тепловоз массой m разгоняется из состояния покоя по горизонтальному пути в течение t секунд под действием силы тяги F , после чего до остановки движется с выключенным двигателем. Коэффициент сопротивления движению 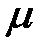 . Определить с каким ускорением двигался локомотив при разгоне, какой скорости он достиг во время разгона, на каком расстоянии от начала движения он остановился ?
. Определить с каким ускорением двигался локомотив при разгоне, какой скорости он достиг во время разгона, на каком расстоянии от начала движения он остановился ? 
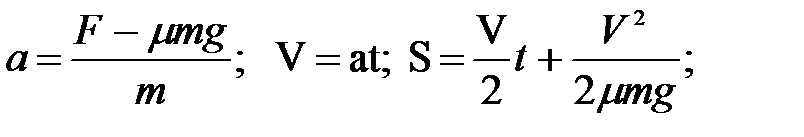
где m=120 т; t=50 с; 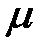 =0,005;
=0,005;
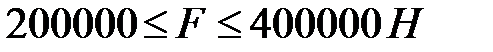 с шагом 5000 Н;
с шагом 5000 Н;
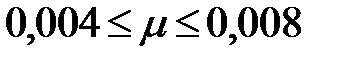 с шагом 0,002
с шагом 0,002
Вариант 17
1. К пружине подвешен груз массой m. Пружина под влиянием силы F растягивается на величину x .Определить период вертикальных колебаний груза для разных F :
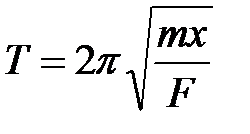 .
.
Отладить программу для следующих значений переменных:
m=10 кг; х=0,15 м; 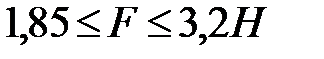 с шагом 0,15 Н.
с шагом 0,15 Н.
2. Работая на максимальной мощности, тепловоз ведет поезд массой m вверх по пути с уклоном L1 со скоростью V1. Работая на 60% мощности, тепловоз ведет тот же поезд вверх по пути с уклоном L2 со скоростью V2. Найти максимальную мощность тепловоза и коэффициент трения:
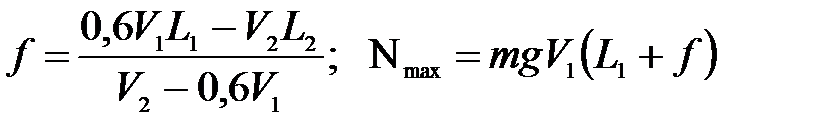 ,
,
где m=2000 т; V2=50 км/ч ; L2=0,003;
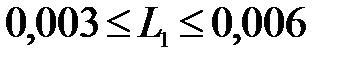 с шагом 0,001;
с шагом 0,001;
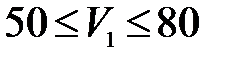 км/ч с шагом 10 км/ч.
км/ч с шагом 10 км/ч.
Вариант 18
1.Определить смещение точки, совершающей гармоническое колебание
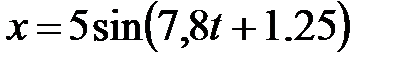 ,
,
где 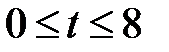 с шагом 0,5 с.
с шагом 0,5 с.
2. Какую максимальную работу надо совершить, чтобы поднять вагонетку с углем массой m по эстакаде длинной l и высотой h при коэффициенте трения 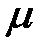 ? Каков КПД подъемника?
? Каков КПД подъемника?
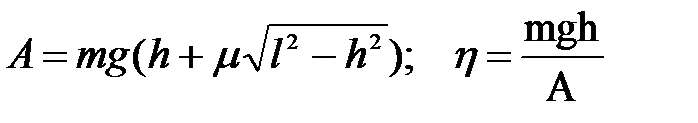 ,
,
где m=200кг; 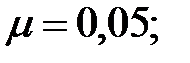
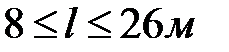 с шагом 3м;
с шагом 3м;
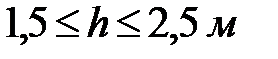 с шагом 25см.
с шагом 25см.
Вариант 19
1. Координаты точки при переходе от общих осей координат к другим, наклоненным к первым под углом L, определяются по формулам:
 x1=xCosL+ySinL; y1=-xSinL+yCosL.
x1=xCosL+ySinL; y1=-xSinL+yCosL.
Как будут меняться координаты x1 и y1 для точки x=2,7; y=3,4, если 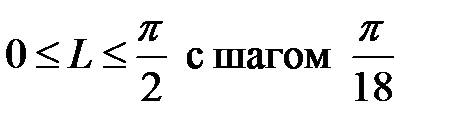 .
.
2. Два поезда прошли одинаковый путь за одно и тоже время. Однако один поезд, трогаясь с места, прошел весь путь равноускоренно с ускорением а, другой поезд половину пути шел со скоростью V1, а другую со скоростью V2. Найти путь, пройденный поездами.
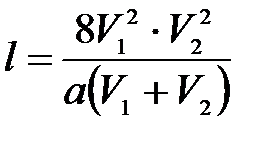 ,
,
где V1=20 км/ч;
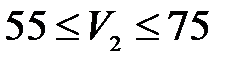 км/ч с шагом 10 км/ч;
км/ч с шагом 10 км/ч;
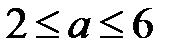 см/c2 с шагом 1 см/c2.
см/c2 с шагом 1 см/c2.
Вариант 20
1.Определить число зон пригородного пассажиропотока при составлении расписаний движения поездов по формуле:
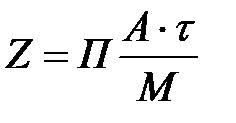 ,
,
где П - общее число остановочных пунктов на участке;
А - среднечасовой пассажиропоток на остановочном пункте;
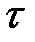 - время на разгон, замедление и стоянку поезда;
- время на разгон, замедление и стоянку поезда;
M - расчетная населенность поезда.
Для отладки принять: П=12; 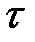 =0,5 ч; А=3,0 тыс.чел.
=0,5 ч; А=3,0 тыс.чел.
1000 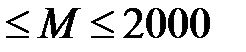 чел;
чел; 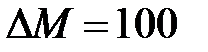 чел;
чел;
2. Поезд массой m при торможении с ускорением а останавливается через время t после начала торможения. Какое количество тепла выделится при торможении?
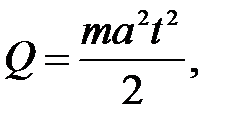
где m =2000 т; 0,1 £ а £ 0,7 м/с2 с шагом 0,15 м/с2 ;
30 £ t £ 50 с шагом 10 с.
Вариант 21
1. Определить диаметр d и длину l цилиндрической стальной цапфы вала, рассматривая цапфу как балку, заделанную концом. Нагрузка P на квадратную единицу диаметрального сечения цапфы не должна превышать 30 кг/см2; допускаемое напряжение R=800 кг/см; полная величина давления на цапфу Q 20 £Q £27 т с шагом 0,5 т
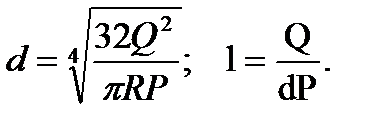
2.Локомотив на горизонтальном участке пути развивает постоянную силу тяги FТ . На участке пути длиной l скорость поезда возросла с V1 до V2. Определить коэффициент трения.
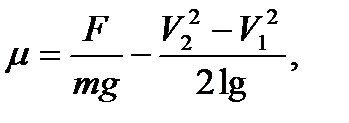
где V1 = 10 м/c; g = 9,81 м/c2; F = 200 кН; l = 4000 м;
106 £ m £ 3×106 кг с шагом 0,5×106 кг;
20 £ V2 £ 50 м/c с шагом 10 м/с.
Вариант 22
1.Найти расстояние между точками, совершающими гармонические колебания
x1=0,1×Sin2t ; x2=1,7×Sin(0,8t-0,42)
в момент времени 0,6 £ t £ 1,8 с шагом 0,2.
2.Вагонетка массой m поднимается по рельсам в гору, наклон которой L c ускорением a. Коэффициент трения m. Какую работу при подъеме совершит сила тяги на пути x?
A=mx[a+g(sinL+mcosL)],
где m=3000 кг; a= 0,2 м/с2; x = 50м; g = 9,81м/с2;
10° £ L £ 30° с шагом 5°;
0,05 £ m £ 0,1 с шагом 0,01.
Вариант 23
1.Какова в зависимости от дальности поездки оптимальная для пассажиров длина перегона на пригородных участках движения поездов?
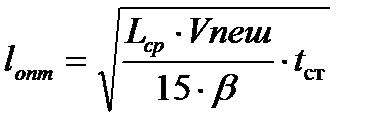 ,
,
где Lср - средняя дальность поездки пассажира в пригородном сообщении;
Vпеш - средняя скорость передвижения пешеходов;
tст - стоянка поезда с учетом затрат времени на разгон и торможение;
Отладку программы произвести для значений
b = 1,5; Vпеш = 5 км/ч; tст = 1 м; 20 £ Lср £ 40 км с шагом 2,5км.
2.Два вагона с массами m1 и m2 скатываются с горки , сталкиваются со скоростями U1 и U2 и автоматически сцепляются. Определить скорость вагонов после удара.
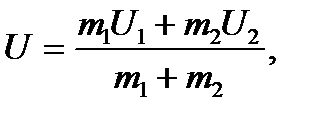
где U1 = 5,3 м/c; U2 = 2,7 м/c;
20 £ m1 £ 100 т с шагом 20т;
20 £ m2 £ 100 т с шагом 20т.
Вариант 24
1.С расстояния d фотографируют поезд, движущийся со скоростью V. Определить для разных объективов время t экспозиции, за которое изображение сместилось бы не более чем S=0,01 мм. Фокусное расстояние объектива F.
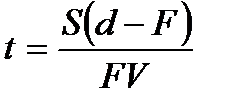

Отладку программы выполнить для контрольного примера :
V = 72 км/ч; d=100 м; F=22 мм, 37 мм, 50 мм, 80 мм, 140 мм.
2. Вагон массой m1, движущийся по горизонтальному пути со скоростью V1, автоматически на ходу сцепляется с неподвижным вагоном массой m2. С какой скоростью движутся вагоны после сцепления ?
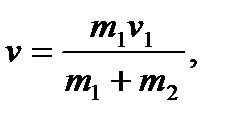
где v1 = 1,5 м/с; 10 £ m1 £ 40 т с шагом 10 т
10 £ m2 £ 40 т с шагом 10 т.
Вариант 25
1. Отклонения при свободных затухающих колебаниях описываются формулой:
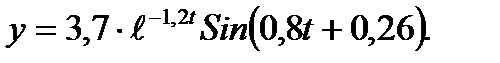
Найти расстояние от начала координат до точек на этой кривой в момент времени t=0, 2 , 4, 6,...24 по формуле
Z= 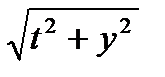 .
.
Результаты решения представить в виде таблицы.
2 . На каком минимальном расстоянии от закрытого светофора машинист должен начать тормозить состав, движущийся со скоростью V км/ч. Коэффициент трения между колесами и рельсами m.
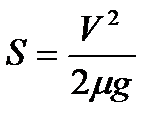 ,
,
где g = 9,81 м/c2;
30 £ V £ 150 км/ч с шагом 20 км/ч;
0,02 £ m £ 0,06 с шагом 0,02.
Вариант 26
1.Какое количество условного топлива израсходуют двигатели тепловоза на расстоянии l при изменении скорости V ,если средняя мощность его двигателя P=2000 кВт, а КПД η =25%.. Tеплота сгорания условного топлива g=2,8×107 Дж/кг.

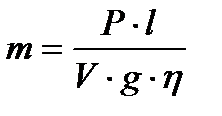 .
.
Отладить программу для значений
l = 100 км; 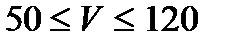 км/ч с шагом 10км/ч.
км/ч с шагом 10км/ч.
2. На сколько должен быть поднят наружный рельс над внутренним на кривой радиуса R ,чтобы при скорости движения V силы давления поезда на оба рельса были одинаковыми и рельсы не подвергались сдвигу? Ширина колеи S =1520 мм.

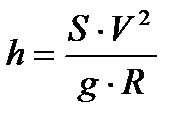 ,
,
где 60 £ V £ 140 км/ч с шагом 40 км/ч;
500 £ R £ 2000 м с шагом 250 м.
Вариант 27
1. Маховик , вращаясь с постоянной угловой скоростью wo был отключен от двигателей и, сделав m оборотов, остановился .Найти угловое ускорение маховика.
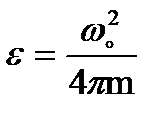
Отладить программу для значений:
wo = 650 рад/с; 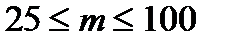 об. с шагом 5 об.
об. с шагом 5 об.
2. Вагон массы m1 c автоматической сцепкой , движущийся со скоростью u1 , догоняет такой же вагон массы m2 , движущийся со скоростью u2 , и сцепляется с ним . Двигаясь дальше вместе оба вагона сталкиваются со стоящим на рельсах третьим вагоном массы m3 .Найти скорости движения вагонов на разных участках пути . Трением пренебречь. 
u4 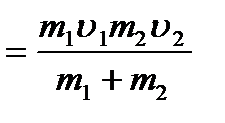 ; u5
; u5 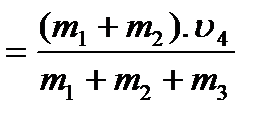 ,
,
где u1 = 12 м/с; u2 = 6 м/с; m3 = 40 т;
20 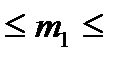 60 т с шагом 10т;
60 т с шагом 10т;
20 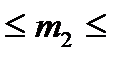 60 т с шагом 10т.
60 т с шагом 10т.
Вариант 28
1. Паровой молот массой m1 падает с высоты h на стальную болванку массой m2 .Cколько раз он должен упасть, чтобы температура болванки поднялась на  t0C ? На нагрев болванки идет 50% теплоты, полученной при ударах. Удельная теплоемкость стали С = 460 Дж/кгН.
t0C ? На нагрев болванки идет 50% теплоты, полученной при ударах. Удельная теплоемкость стали С = 460 Дж/кгН.
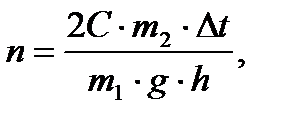
где g = 9,81 м/с2; h = 2,5 м, 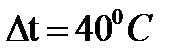 , m2 = 220 кг
, m2 = 220 кг
6 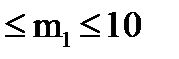 т с шагом 0,5 т.
т с шагом 0,5 т.
2. Мимо наблюдателя, стоящего на платформе, проходит поезд. Первый вагон поезда прошел мимо наблюдателя за время t1 , второй - за время t2. Найти
скорость поезда в начале и в конце наблюдения, а также ускорение поезда, считая движение поезда равнопеременным. Длина каждого вагона l=12 м.
Vн= 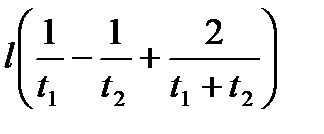 ; Vк=
; Vк= 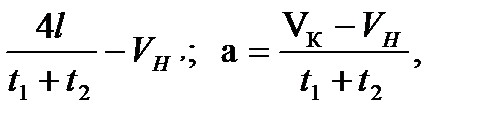
где 0,5 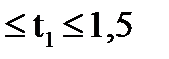 с шагом 0,25 с; 0,8
с шагом 0,25 с; 0,8 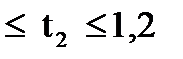 с шагом 0,1 с.
с шагом 0,1 с.
Вариант 29
1. По прямому участку пути двигаются три вагона с массами m1,m2,m3.Какое максимальное число столкновений между ними может произойти 
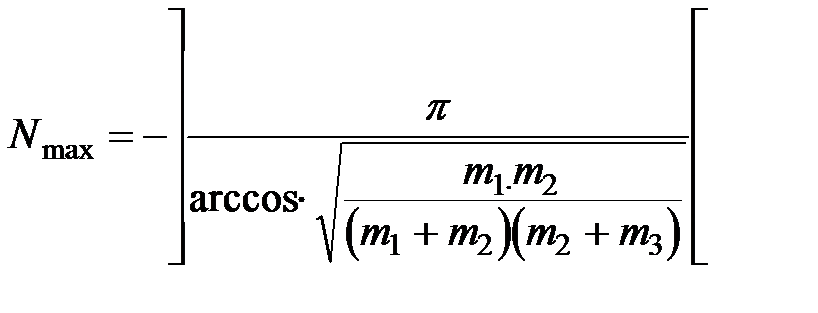 ;
;
где: 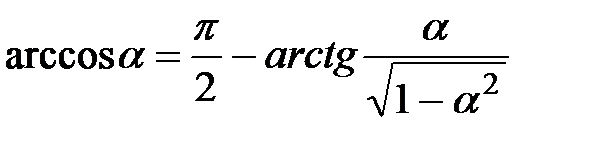 ;
; 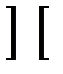 -целая часть числа;
-целая часть числа;
m 1= 100 т; m3 = 100 т; 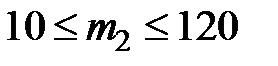 т с шагом 10 т.
т с шагом 10 т.
2. Поезд, имея скорость Vo, стал двигаться равнозамедленно и через время t снизил скорость до V. С каким ускорением двигался поезд на этом участке? Какой он при этом прошел путь?

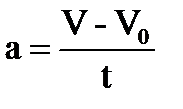 ;
; 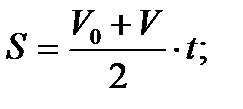
где 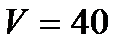 км/ч;
км/ч; 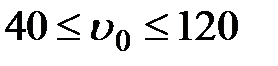 км/ч с шагом 20 км/ч;
км/ч с шагом 20 км/ч;
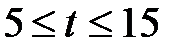 с с шагом 2,5 с.
с с шагом 2,5 с.
Вариант 30
1. Груз массы m поднимается лебедкой с ускорением a. Найти работу, произведенную за первые t секунд от начала подъема: 

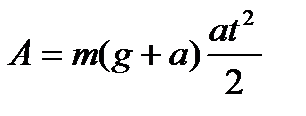
Для отладки программы принять: 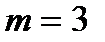 т,
т, 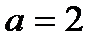 м/с
м/с 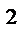 ,
,
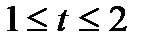 , с шагом
, с шагом 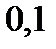 с.
с.
2.Скорость поезда между двумя пунктами V1, средняя скорость на всём пути V2, причём остановки занимают время tост. Найти расстояние L между этими пунктами и время в пути
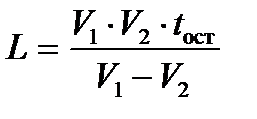 ;
; 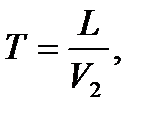
где tост = 1ч; 80 £ V1 £ 120км/ч с шагом 10 км/ч;
50 £ V2 £ 70 км/ч с шагом 5 км/ч.
Вариант 31
1. При быстром торможении трамвай, имевший скорость V, начал двигаться “юзом”. Определить расстояние, которое пройдет трамвай с момента торможения до полной остановки. Коэффициент трения между колесами и рельсами - k.
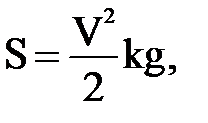
Если 10 £ V £ 50 км/ч c шагом 5 км/ч; k=0,2; g=9,80665 м/сек2.
2. Найти полную поверхность правильной треугольной пирамиды по данному ее объему V и углу L между боковой гранью и плоскостью основания:
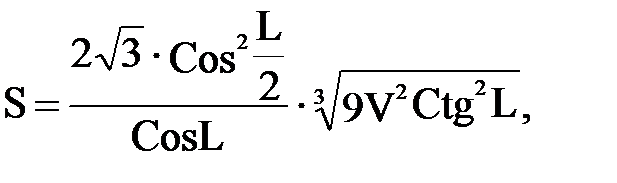
если 800 £ V £ 950 см3 с шагом 50 см3 ;
0,5 £ L £ 0,7 рад. с шагом 0,1 рад.
Вариант 32
1. В прямоугольной пирамиде двугранный угол при основании равен a Определить наклон бокового ребра к плоскости основания пирамиды по формуле:
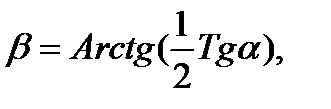
если 300 £ α £ =600 с шагом 30.
Результат напечатать в градусной мере.
2. По неподвижной наклонной плоскости, образующей угол α с горизонтом, начинает соскальзывать без трения тело массой m1. На расстоянии L от начала движения в него попадает тело массой m2, летящее горизонтально. При этом тела останавливаются. Определить скорость второго тела до удара по формуле:
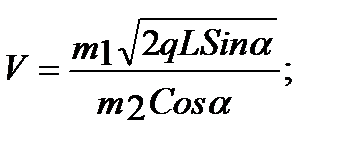
Если 0,1 £ m1 £ 0,5 кг c шагом 0,1;
0,1 £ m2 £ 0,5 кг c шагом 0,1;
L=1,2 м; α=0,5 рад; q=9,81 м/с2.
Вариант 33
1. Найти радиус основания цилиндра, имеющего при данном объеме наименьшую поверхность:
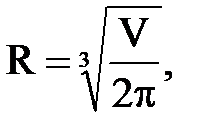
если 150 £ V £ 750 см3 с шагом 50 см3.
2. Объем правильной четырехугольной пирамиды равен V. Боковые грани пирамиды наклонены к плоскости основания под углом L. Определить полную поверхность пирамиды по формуле:
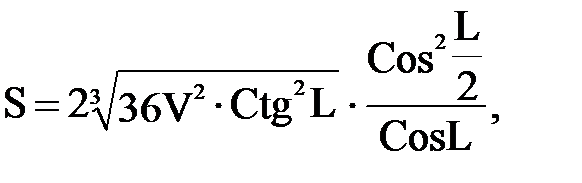
если 500 £ V £ 1000 см3 с шагом100 см3;
0,2 £ L £ 0,8 рад c шагом 0,2 рад.
Вариант 34
1. Исследовать поведение функции y=5x2-3x-10 в диапазоне от -4 до 4, с шагом изменения аргумента в 0,5.
2. Напечатать таблицу умножения чисел от 1 до 9.
Вариант 35
1. Напечатать таблицу перевода мер длины из метров в сажени, футы и аршины от 1 до 10, если 1 сажень равна 2,1366 м, 1 фут равен 0,3048 м и 1 аршин равен 0,7112 м.
2. Как изменяются площадь S и периметр P прямоугольного треугольника при изменении значения катета А от начального значения А0 до конечного значения АК с шагом ΔА и значения катета В от начального значения В0 до конечного значения ВК с шагом ΔВ,
если S = 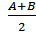 , а P = A + B + C где С =
, а P = A + B + C где С = 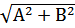
Для отладки принять А0 = 4, АК = 10, ΔА = 2, В0 = 20, ВК = 30 и ΔВ = 5.
5. Содержание отчета
Отчет по лабораторной работе № 4 полностью оформляется в текстовом процессоре Word, размер шрифта 12, распечатывается и сшивается.
Отчет должен содержать все основные этапы подготовки и решения задач. Тексты программ копируются в отчет после их отладки. Результаты решения представляются в виде скриншотов и подтверждаются ручным расчетом контрольных примеров для трех вариантов значений аргументов.
Приложение А
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Государственное бюджетное образовательное учреждение
высшего образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»
Кафедра «ИНФОРМАТИКА И ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ»
Дисциплина: «Информатика»
ОТЧЕТ
по лабораторной работе № 2
«СТРУКТУРА СЛЕДОВАНИЕ»
Вариант X
Выполнил студент Иванов И.И.
Факультета XXX
Группы XXX-000
Санкт-Петербург
20__
Задание 1.
Математические формулы, заданные в левом столбце представить в правом столбце в виде операторов присваивания на языке Visual Basik
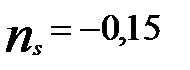
| Ns = -0.15 |
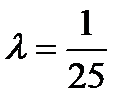
| lambda=1/25 |
| π = 314∙10-2 | pi=314E-2 |
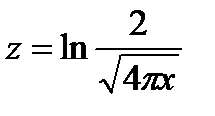
| Z = log(2/(sqr(4*pi*x))) |
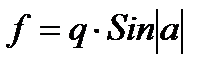
| F = q*sin(abs(a)) |
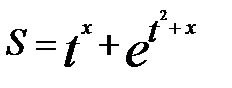
| s=t^x+Exp(t^2+x) |
Задание 2.
1. Постановка задачи
Найти длину окружности L заданную радиусом, если радиус R = 10 см.
Входные данные:
R – радиус окружности, переменная вещественного типа,
π = 3,14 – константа вещественного типа.
Выходные данные:
L – длина окружности , переменная вещественного типа.
2. Математическая модель задачи
L = 2πR
3. Разработка алгоритма
| 1 |
| 2 |
| 4 |
| 5 |
| 6 |
| 3 |
| Начало |
| Конец |
| π = 3,14 |
| R |
| R, L |
| L=2 π R |
4. Разработка визуальной части проекта
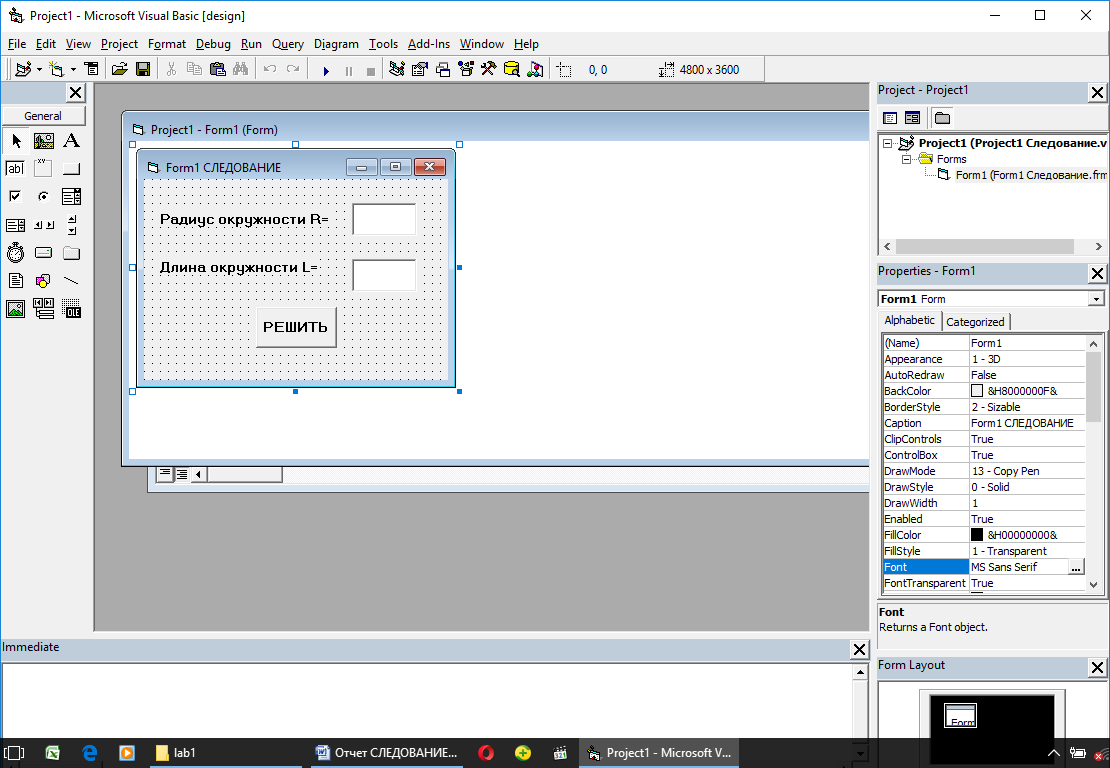
5. Код приложения
Private Sub Command1_Click()
Dim R As Single, L As Single
Const Pi As Single = 3.14
R = Val(Text1.Text)
L = 2 * Pi * R
Text2.Text = Str(L)
End Sub
6. Отладка приложения :
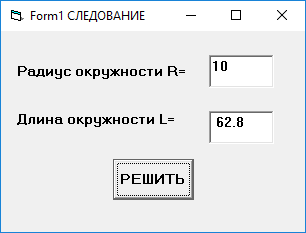
Ручной счет:
При R = 10 L = 62,831
Приложение Б
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Государственное бюджетное образовательное учреждение
высшего образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»
Кафедра «ИНФОРМАТИКА И ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ»
Дисциплина: «Информатика»
ОТЧЕТ
по лабораторной работе № 3
«СТРУКТУРА РАЗВИЛКА»
Вариант X
Выполнил студент Иванов И.И.
Факультета XXX
Группы XXX-000
Санкт-Петербург
20__
Задание 1
1. Постановка задачи:
Дано действительное число X, являющееся аргументом функции Y=Sin X, если оно отрицательно и функции Y = X2 - если положительное.
Входные данные:
X – аргумент функции, переменная вещественного типа
Выходные данные:
Y – значение функции, переменная, вещественного типа
2. Математическая модель задачи
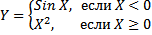
3. Разработка алгоритма :
| 1 |
| Начало |
| 6 |
| 2 |
| Да |
| Нет |
| X |
| Y = X2 |
| X, Y |
| Конец |
| 3 |
| 5 |
| 4 |
| 7 |
| X < O |
| Y = Sin X |
4. Разработка визуальной части проекта:
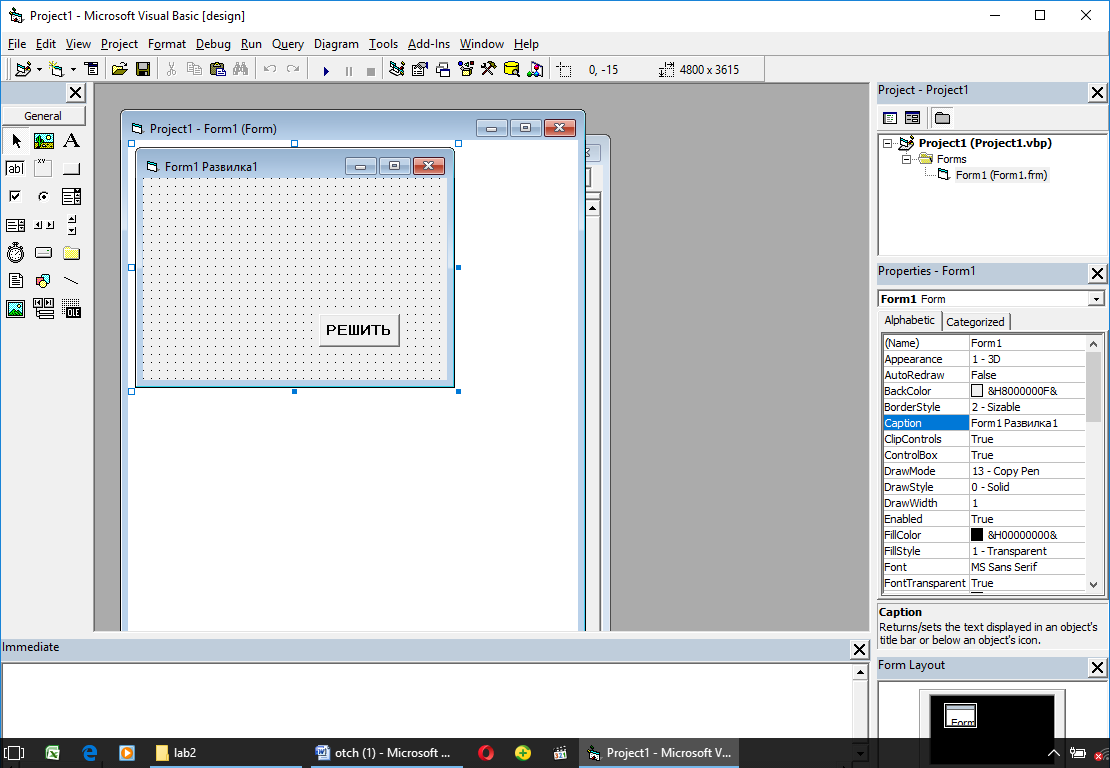
5. Код приложения :
Private Sub Command1_Click()
Dim x As Single, y As Single
x = InputBox("x=")
If x < 0 Then
x = Sin(x)
Else
x = x ^ 2
End If
Print "x=" & x, " y=" & y
End Sub
6. Отладка программы:
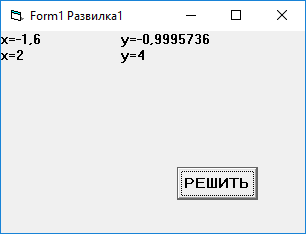
Результаты ручного счета:
При Х = -1,6 Y = Sin X = -0,99
При X = 2 Y = X2 = 4
Задание 2
1. Постановка задачи
Для заданного значения аргумента вычислить значение функции, заданной графиком.
| P |
| t |
Входные данные:
t – аргумент функции, переменная вещественного типа.
Выходные данные:
t – аргумент функции, переменная вещественного типа,
P – значение функции, переменная вещественного типа.
2. Математическая модель задачи:

3. Разработка алгоритма
| Нет |
| Нет |
| Да |
| Да |
| x, y |
| P = 0 |
| 0≤t≤2,5 |
| 3 |
| 2 |
| t |
| 1 |
| Начало |
| t<0 |
| 4 |
| 6 |
| P = -1 |
| 5 |
| 7 |
| 8 |
| P = 1 |
| 9 |
| Конец |
4. Разработка визуальной части проекта
5. Код приложения
Private Sub Command1_Click()
Dim t As Single, P As Single
t = InputBox("t=")
If t < 0 Then
P = -1
ElseIf 0 <= t And t <= 2.5 Then
P = 0
Else
P = 1
End If
Print " t=" & t & " P=" & Format(P, "0.00")
End Sub
6. Отладка программы:
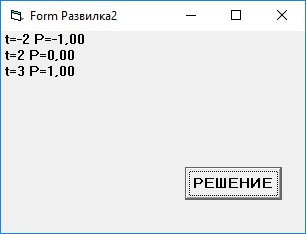
Полученные результаты соответствуют графику.
Приложение С
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Государственное бюджетное образовательное учреждение
высшего образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»
Кафедра «ИНФОРМАТИКА И ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ»
Дисциплина: «Информатика»
ОТЧЕТ
по лабораторной работе № 4
«СТРУКТУРА ЦИКЛ»
Вариант X
Выполнил студент Иванов И.И.
Факультета XXX
Группы XXX-000
Санкт-Петербург
20__
Задание 1
1.Постановка задачи
Вычислить значения функции Y = Cos X для всех X , принимающих значения от 0 до 1,0 c шагом 0,1
Входные данные: X0 – начальное значение параметра цикла,
вещественная переменная;
Xk – конечное значение параметра цикла,
вещественная переменная;
dX – шаг параметра цикла,
вещественная переменная.
Выходные данные: X - параметр цикла, вещественная переменная;
Y- значение функции, вещественная переменная.
2.Математическая модель
Y = Cos X , при X0 ≤ X ≤ Xk с шагом dX
3. Разработка алгоритма
| 1 |
| 2 |
| 3 |
| 4 |
| 8 |
| 5 |
| 6 |
| 7 |
| Начало |
| X0, Xk, dX |
| X = X0 |
| X ≤ Xk |
| Y = Cos X |
| X, Y |
| X = X + dX |
| Конец |
| Нет |
| Да |
4.Разработка визуальной части проекта
5. Код приложения
Private Sub Command1_Click()
Dim X As Single, Y As Single
Dim X0 As Single, Xk As Single, dX As Single
X0 = InputBox("Введите X0")
Xk = InputBox("Введите Xk")
dX = InputBox("Введите dX")
List1.AddItem (" X Y")
For X = X0 To Xk + dX / 2 Step dX
Y = Cos(X)
List1.AddItem (Format(X, "0.000") & " " & Format(Y, "0.000"))
Next
End Sub
6.Отладка программы
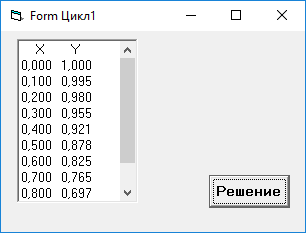
Ручной счет:
При Х = 0, Y = 1,0
X = 0,5 Y = 0,877
X = 0,8 Y = 0,696
Задание 2
1. Постановка задачи
Вычислить значения функции двух переменных Z = Sin X + Cos Y при изменении аргументов в заданных пределах и с заданными значениями шага для каждого из них.
Входные данные: Xo, Xk, Yo, Yk - начальные и конечные значения
параметров цикла,
dX, dY – значения шага параметров цикла,
вещественные переменные.
Выходные данные: X, Y, Z – значения аргументов и функции,
вещественные переменные.
2.Математическая модель
Z = Sin X + Cos Y,
где Xo ≤ X ≤ Xk с шагом dX
Yo ≤ Y ≤ Yk с шагом dY
3.Разработка алгоритма
Внешний цикл с предусловием, внутренний с постусловием.
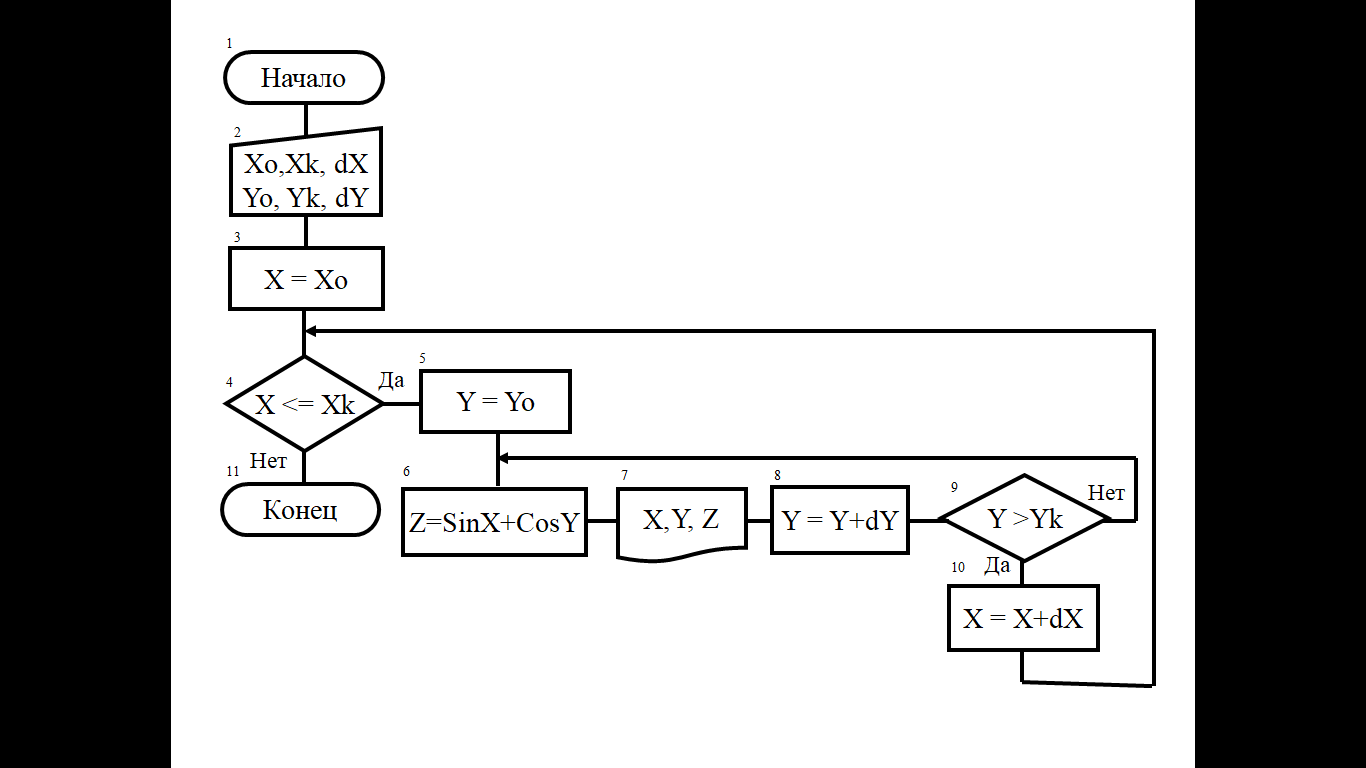
4.Разработка визуальной части проекта
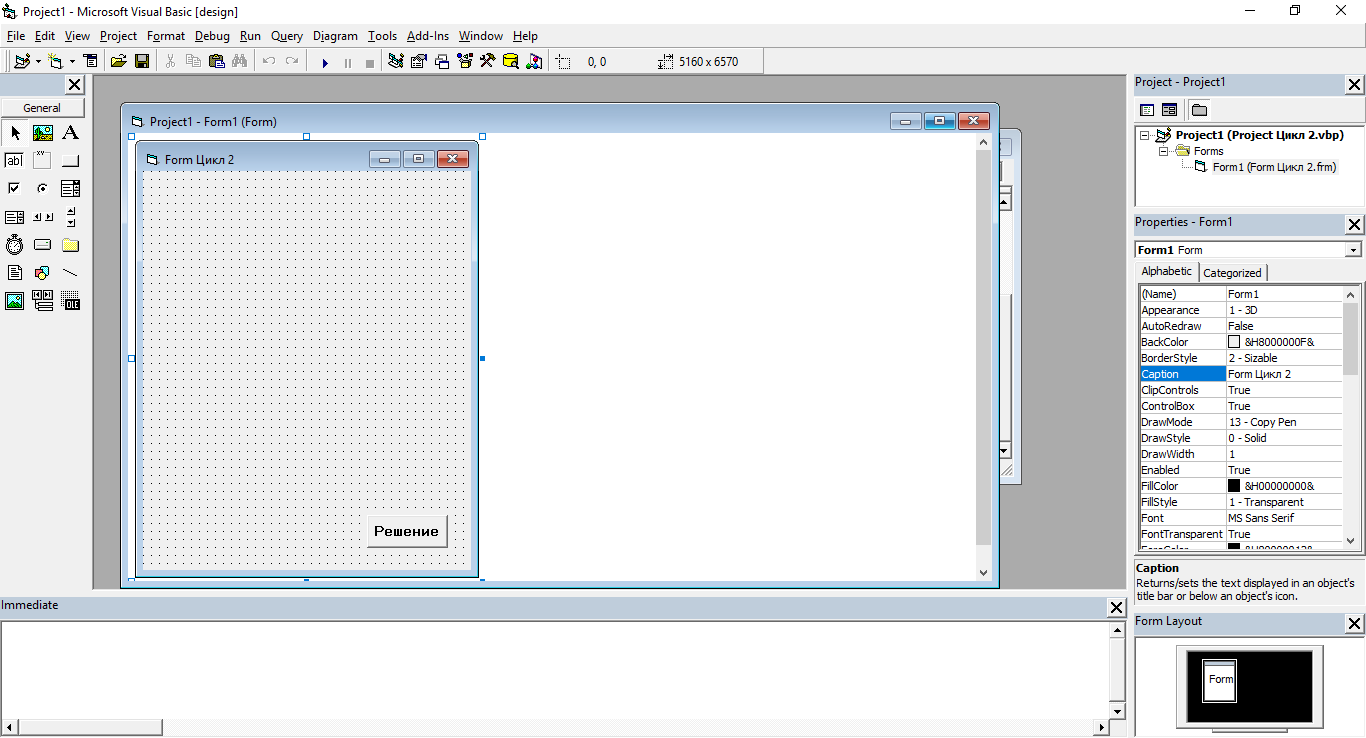
4. Код приложения
Private Sub Command1_Click()
Dim X As Single, Y As Single, Z As Single
Dim X0 As Single, Xk As Single, dX As Single
Dim Y0 As Single, Yk As Single, dY As Single
X0 = InputBox("Введите X0")
Xk = InputBox("Введите Xk")
dX = InputBox("Введите dX")
Y0 = InputBox("Введите Y0")
Yk = InputBox("Введите Yk")
dY = InputBox("Введите dY")
Print " X Y Z"
Print "____________________________________"
X = X0
Do While X <= Xk
Y = Y0
Do
Z = Sin(X) + Cos(Y)
Print X, Y, Z
Y = Y + dY
Loop Until Y > Yk
X = X + dX
Loop
End Sub
5.Отладка приложения
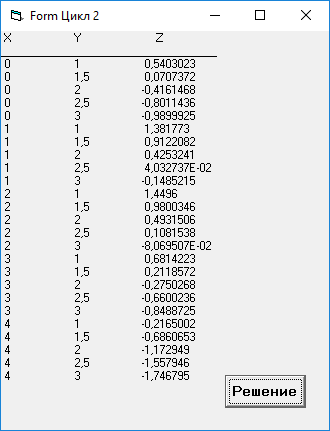
Ручной счет:
при X = 0 и Y = 3 Z = 9,989
при X = 2 и Y = 1,5 Z = 0,980
при Х = 4 и Y = 3 Z = -1,746








