Лабораторная работа № 3
«Структура развилка»
1. Цель выполнения работы
Изучить и сравнить особенности построения алгоритмов и разработки программ алгоритмических структур «Классическая развилка», «Модифицированная развилка», «Вложенная развилка» и «Развилка с одной ветвью».
2. Основные сведения из теории
Для выполнения лабораторной работы и ответа на контрольные вопросы рекомендуется использовать конспект лекций и электронный учебник.
3. Порядок выполнения работы
В каждом варианте задания необходимо выполнить постановку задачи, определить требуемые входные и выходные данные для решения задач. Разработать математические модели, схемы алгоритмов и программы. Предусмотреть печать входных и выходных данных. Значения входных данных выбрать самостоятельно для каждой ветви задания. Вручную просчитать контрольные примеры для каждой ветви алгоритма. Отладить программы и оформить отчет.
4. Задания
Вариант 1
1.
Sinx , если x > p
F =
ex Sinx , если x <= p
2.
Вариант 2
1. Дано действительное число. Возвести его в квадрат, если оно положительно, и в четвертую степень — отрицательное.
2.
Вариант 3
1.
Ln (1 +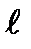 
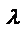) , если x > 1
Y =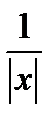 
, если x < =1
2.
Вариант 4
1. Даны две точки А(х1, у1) и В(х2, у2). Определить, которая из точек находится ближе к началу координат. При равных расстояниях ближней считать точку А.
2.
Вариант 5
1.
Z1=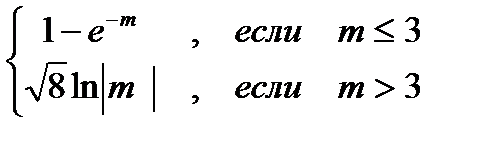 
где m = x3
2.
Вариант 6
1. Даны два угла треугольника (в градусах). Определить, существует ли такой треугольник.
2.
Вариант 7
1.
q =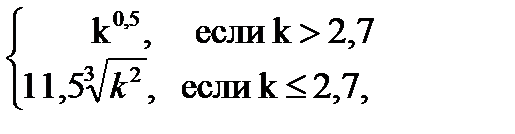 
где к =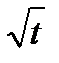 
2.
Вариант 8
1. Даны действительные числа х и у, не равные друг другу. Меньшее из этих двух чисел заменить половиной их суммы, а большее — их удвоенным произведением.
2.
Вариант 9
1. 
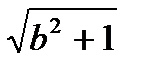, если b £ 10
C =
Ln10 × Lgb , если b > 10, где b = qa
2.
Вариант 10
1. На плоскости ХОY над осью Х задана своими координатами точка А. Определить, в каком квадранте она расположена.
2.
Вариант 11
1.
c 0,6 × ½d½ , если c > 5
Y =
12 × Tg c , если c £ 5 , где c = q + 1
2.
Вариант 12
1. Даны неравные целые числа d и f. Заменить меньшее из них большим, а большее нулём.
2.
Вариант 13
1.
(1 - x) (1 + x) , если x < 0
y =
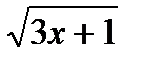, в остальных случаях
2.
| y=2x*sin(x) |
Вариант 14
1. Услуги телефонной сети оплачиваются по следующему правилу: за разговоры до T минут в месяц — A руб., а разговоры сверх установленной нормы оплачиваются из расчета B руб. за минуту. Определить плату за пользование телефоном для введенного времени X разговоров за месяц.
2.
Вариант 15
1.
x Lnx , если x > 5,2
F =
x3 , если x £ 5,2
2.
Вариант 16
1. Грузовой автомобиль выехал из одного города в другой со скоростью V1. Через время t в этом же направлении выехал легковой автомобиль со скоростью V2. Определить, догонит ли легковой автомобиль грузовой через время t1 после своего выезда.
2.
Вариант 17
1.
Sinx , если x <0
Y = Ln (1 + x2) , если x ³ 0
2.
Вариант 18
1. Перераспределить значения переменных х и у так, чтобы в х оказалось большее из этих значений, а в у — меньшее.
2.
Вариант 19
1.
Lg a , если a > 1,3
R =
2,5a - 11 , если a £ 1,3 где a = d + 3,5c
2.
Вариант 20
1. Разработать модель пожарного датчика в помещении, которая выводит сообщение «Пожароопасная ситуация», если температура в комнате превысила 60° С.
2.
Вариант 21
1.
2c - 1 , если c > 4,5
z =
1 + c3 , если с £ 4,5 , где c = 1,5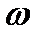 
2.
Вариант 22
1. Продукты расфасованы в два пакета. Масса первого — m1 кг, второго — m2 кг. Определить какой пакет тяжелее — первый или второй и массу более тяжелого пакета.
2.
Вариант 23
1. Y =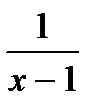 
, если x > 1
Sin x , если x <=1
2.
Вариант 24
1. Определить пройдет ли график функции у = ах2 + bх + с через заданную точку с координатами (g, h).
2.
Вариант 25
1. Sin x , если x > 0
F =
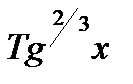, если x £ 0
2.
Вариант 26
1. Даны действительные числа а, b, с. Удвоить эти числа, если а ≥ b ≥ с, и заменить их абсолютными значениями, если это не так.
2.
| 0 |
| 0.5 |
| 1 |
| 1.5 |
| 2 |
| 2.5 |
| 3 |
| 3.5 |
| 4 |
| -1.8 |
| -1.5 |
| -1.2 |
| -1 |
| -0.6 |
| -0.3 |
| 0 |
| 0.3 |
| 0.6 |
| 1 |
| 1.2 |
| 1.5 |
| 1.8 |
| y=|x| |
| y=1/x |
| y= x |
Вариант 27
1.
x Sin x , если x > p или x < - 2p
Y =
Sin x , если -2p £ x £p
2.
| -2 |
| -1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| -3.0 |
| -2.5 |
| -2.0 |
| -1.5 |
| -1.0 |
| -0.5 |
| 0.0 |
| 0.5 |
| 1.0 |
| 1.5 |
| 2.0 |
| 2.5 |
| 3.0 |
| 3.5 |
| 4.0 |
| y=1/|x| |
| y=1 |
| y=ln(e |
| x |
| ) |
Вариант 28
1. На оси ОХ расположены три точки а, b, с. Определить, какая из точек b или с расположена ближе к а.
2.
Вариант 29
1. Lg a , если a > 4
M = L + d , где L =
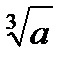, если a 
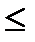4
2.
Вариант 30
1. Определить, не приводит ли суммирование двух целых чисел А и В к переполнению (т.е. к результату большему чем заданная величина С). Если будет переполнение, то сообщить об этом, иначе вывести сумму этих чисел.
2.
Вариант 31
1. 
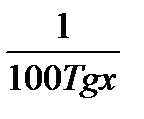+ 4 , если x <= 0
Z=
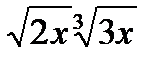, если x > 0
2.
|
|
|
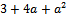
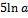
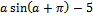
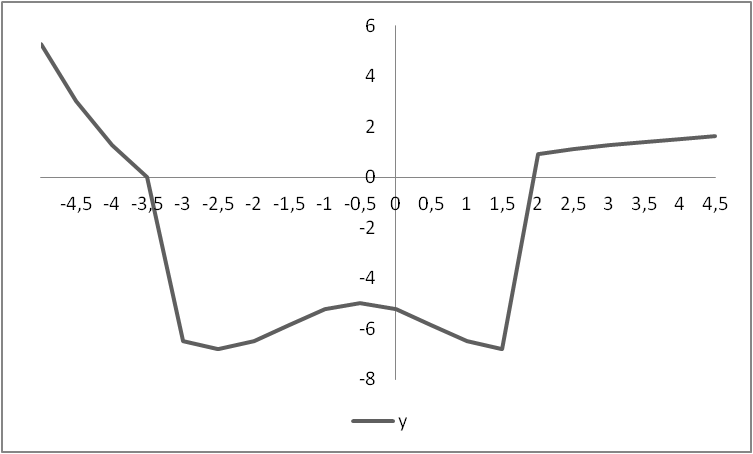
Вариант 32
1 Определить находится ли точка с координатами (x0, у0) внутри окружности радиуса R с центром в точке (x1, y1).
2.
|
|
|
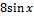
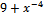
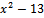
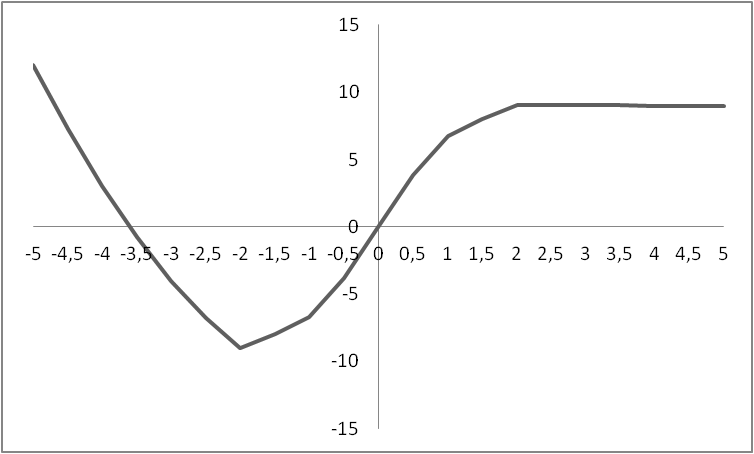
Вариант 33
1.
Lg x , если x > 1
F =
½x2 - 1½ , если x < =1
2.
| -2x-7 |
| x-4,5 |
| Cos x |
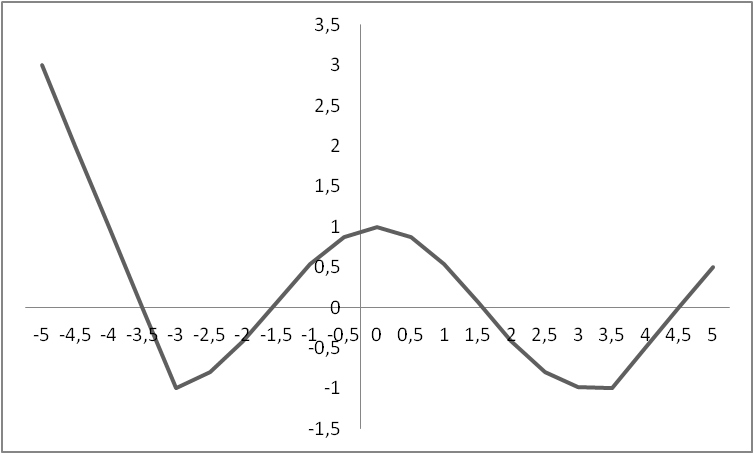
Вариант 34
1. Два отрезка AB и CD расположены на оси X и Y соответственно и заданы своими координатами. Определить какой отрезок длиннее. Координаты задать самостоятельно.
2.
|
|
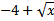
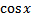
2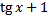 
|
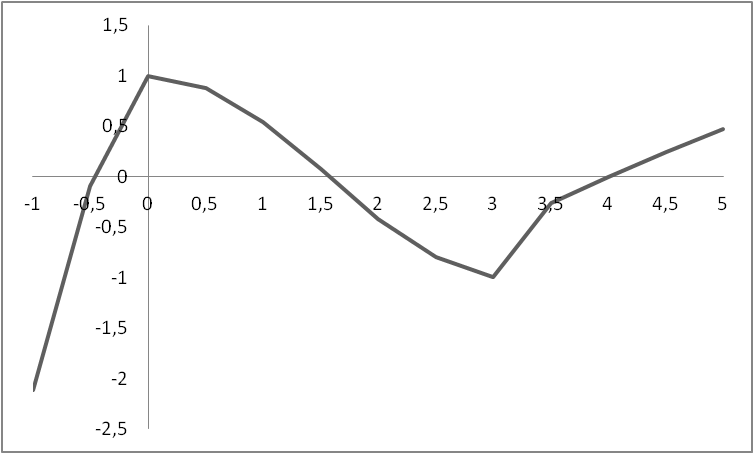
Вариант 35
1. Определить в каком квадранте находится значение функции SinX, если Х>0.
2.
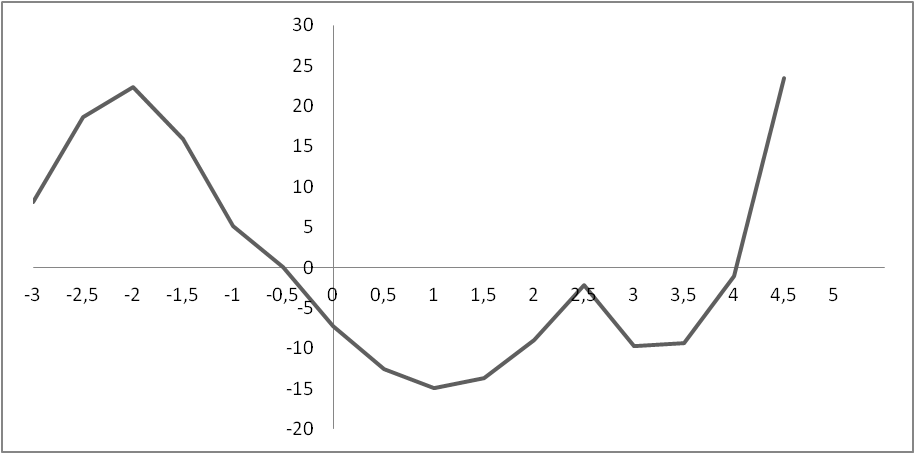
| ex –x3 |
| -15 Sin x |
| 10(1,5 Sin x)2 |
5. Содержание отчета
Отчет по лабораторной работе № 3 полностью оформляется в текстовом процессоре Word, размер шрифта 12, распечатывается и сшивается.
Отчет должен содержать все основные этапы подготовки и решения задач. Тексты программ копируются в отчет после их отладки. Результаты решения представляются в виде скриншотов и подтверждаются ручным расчетом контрольных примеров.