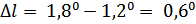Вычислите значение константы в третьем законе Кеплера.
Решение.
Третий закон Кеплера:
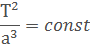
Для движения по круговой орбите его можно переписать так:
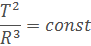
Скорость движения при этом будет равна:
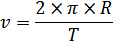
Движение по круговой орбите возможно при условии, что скорость (v) является первой космической:
,
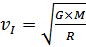где G – гравитационная постоянная, М – масса Солнца, R – радиус орбиты.
Возводя в квадрат правые части двух последних уравнений и приравнивая их, можно получить искомое значение константы третьего закона Кеплера:
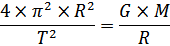
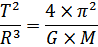
Т.е.
.
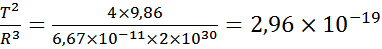
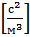Верная запись третьего закона Кеплера – 3 балла.
Верный вывод величины константы – 3 балла.
Верный расчет ее значения – 2 балла.
Арифметическая ошибка в расчете – минус 1 балл.
7 задание.
Искусственный спутник обращается вокруг Земли с периодом 120 минут по круговой орбите, лежащей в плоскости экватора Земли. Как часто можно наблюдать этот искусственный спутник в зените при наблюдении из определенной точки на экваторе Земли? (8 баллов)
Решение
Спутник совершает полный оборот вокруг Земли спутник за 120 минут. Полный оборот вокруг своей оси Земля совершает за звездные сутки, и это означает, что вокруг своей оси Земля вращается с угловой скоростью
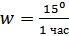. За 120 минут Земля повернется вокруг своей оси на 30º и искусственному спутнику, чтобы вновь оказаться в зените потребуется пройти по своей орбите эти дополнительные 30º. Угловая скорость спутника 
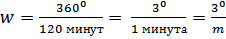. Определим искомое время: 
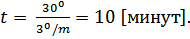Примерный период повторяемости прохождений спутника через зенит составит 120m+10m = 130m.
8 задание.
Найдите отношение сил гравитационного взаимодействия (сил тяготения) Луна-Земля и Солнце-Земля (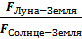 
).
Приливы. Изобразите взаимное расположение Земли, Луны и Солнца для основных фаз Луны (новолуние, первая четверть, полнолуние и третья четверть) и положение приливных горбов.
Укажите в каких из этих положений величина приливов больше, а в каких меньше?
Решение
Сила гравитационного взаимодействия двух тел с массами M и m, находящихся на расстоянии R друг от друга, определяется законом тяготения Ньютона:
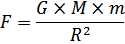
Таким образом, отношение сил взаимодействия Солнце-Земля и Луна-Земля равно
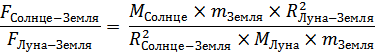
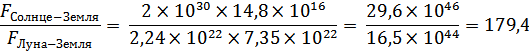
Новолуние:
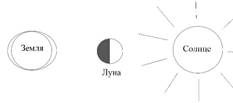
1 четверть:
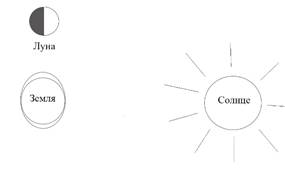
Полнолуние:
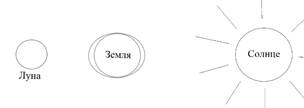
3 четверть:
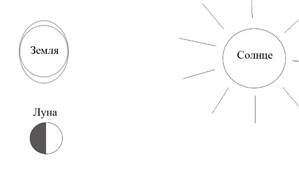
Величина приливов в положениях Луны «1 четверть» и «3 четверть» больше, чем в положениях «Новолуние» и «Полнолуние». Это связано с тем, что в положениях Луны «1 четверть» и «3 четверть» гравитационные влияния Солнца и Луны действуют по одной прямой (сизигийные приливы), а в положениях «Новолуние» и «Полнолуние» - в перпендикулярных направлениях (квадратурные приливы).
10 Задание.
Предельное значение массы груза, который может перемещать транспортный робот при строительстве лунной базы равна 1275 кг. Собственная масса робота 1000 кг. Можно ли использовать этого робота при строительстве базы на Марсе? Ответ обоснуйте количественным расчетом.
Решение.
Вес робота на Луне при полной загрузке составляет:
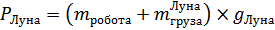
Вес робота при полной загрузке на Марсе составляет
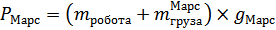
Приравнивая правые части этих соотношений, получаем
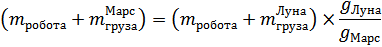
Таким образом,
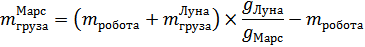
Поскольку ускорение свободного падения на поверхности тела массой М и радиуса R равно
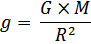
Отношение ускорений свободного падения на Луне и Марс составляет:
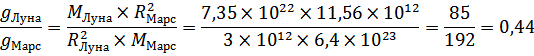
Подставляя в полученное выше уравнение численные значения, находим
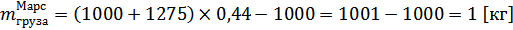
Вывод: для строительства марсианской базы данного робота использовать нецелесообразно, ввиду его малой грузоподъемности.
11 задание .
В поясе астероидов был обнаружен объект с очень высоким альбедо (коэффициентом отражения), движущийся по круговой орбите относительно Солнца на расстоянии от него 1,34 а.е. со скоростью 29,5 км/с. Возникло подозрение, что этот объект – искусственного происхождения. Обоснуйте такую возможность на основе количественного анализа параметров его движения.
Решение.
Движение по круговой орбите естественного объекта Солнечной системы происходит с первой космической скоростью:
,
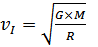где G – гравитационная постоянная, М – масса Солнца, R – радиус орбиты.
Ее значение для указанного радиуса орбиты составляет:
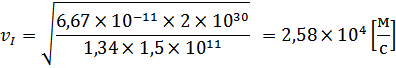
Таким образом, наблюдаемая скорость заметно превышает ту, которую имел бы объект естественного происхождения, движущийся по известным законам:
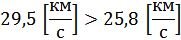
Вывод: предположение о его искусственном происхождении (особенно в сочетании с необычно высоким альбедо) вполне обоснованно.
12 Задание.
Два объекта в области пояса Койпера движутся по круговым орбитам относительно Солнца. Один расположен на расстоянии r 1 = 34,2 а.е., а другой – на расстоянии r 2 = 44,8 а.е. Какой из объектов движется быстрее и чему будет равна разница угловых расстояний между ними за 1 земной год?
Решение.
В соответствии с третьим законом Кеплера
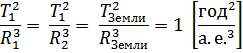
Отсюда
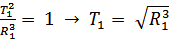
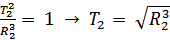, т.е.
= 
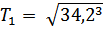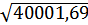= 200 
= 
.
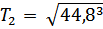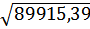
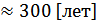Следовательно, за 1 год первый астероид проходит по орбите дугу
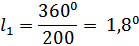
Второй астероид за 1 год проходит по орбите дугу
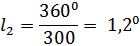
Следовательно, первый астероид движется быстрее, что, разумеется, совершенно естественно, поскольку располагается ближе к Солнцу.
Разница угловых расстояний между объектами за год составляет
