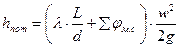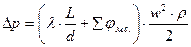Энергетический баланс потока жидкости. Теория подобия.
1) Рассмотрим движение жидкости по трубе с переменным сечением, находящийся над поверхностью сравнительной плоскости. Полный запас энергии жидкости представляет собой сумму потенциальной энергии положения (mgz), потенциальной энергии давления (pv), кинетической энергии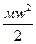 
и внутренней энергии U.
рисунок
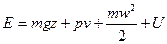( 1 )
где z - высота центра силы тяжести потока над поверхностью сравнительной плоскости, м.
Pассмотрим поток жидкости в сечениях 1-1 и 2-2. Согласно закону сохранения энергии (1 закон термодинамики) полный запас энергии жидкости не изменяется.
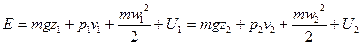(2)
Запишем это уравнение для 1 кг идеальной жидкости
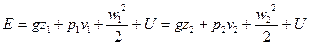(3)
Так как жидкость идеальная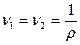 
Разделим все члены уравнения (3) на g
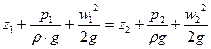– уравнение Бернулли для идеальной жидкости или уравнение энергетического баланса для идеальной жидкости.
z - геометрический напор, м.
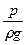- статический или пьезометрический напор, м. Он показывает на какую высоту поднимется жидкость за счет созданного давления.
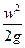- динамический или скоростной напор, м. Он показывает на какую высоту поднимется жидкость за счет кинетической энергии.
Согласно закону Бернулли сумма всех напоров жидкостей есть величина постоянная.
Для реальной капельной жидкости необходимо учитывать действие сил внутреннего трения.
Уравнение Бернулли принимает вид:
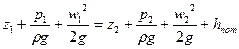
где hпот - потерянный напор, м.
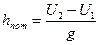
Потерянный напор показывает высоту, на которой жидкость не поднимется, так как часть внутренней энергии израсходована на преодоление внутреннего трения.
Гидродинамическое сопротивление трубопроводов
Реальные жидкости при движении по трубопроводу или аппарату часть энергии затрачивают на преодоление сил сопротивления.
Наличие сил сопротивления обусловлено:
1) наличием сил сопротивления сдвигу, т.е. вязкости жидкости, их называют силами внутреннего трения;
2) наличием местных сопротивлений трубопроводов.
В целом проявление этих сил называют гидродинамическим или гидравлическим сопротивлением трубопровода.
Величина гидравлического сопротивления сил трения зависит от свойств жидкости, шероховатости поверхности трубы и линейной скорости потока, а также от размеров трубы.
рисунок
На величину гидравлического сопротивления будет влиять также режим движения жидкости. Величина гидравлического сопротивления может выражаться в виде потерянного напора или перепада давления, которые характеризуют затраты внутренней энергии. Они рассчитываются по формулам:
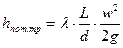
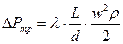
где λ - коэффициент сопротивления трения
L - длина трубопровода
d - диаметр трубы
Величина коэффициента трения определяется по формулам в зависимости от шероховатости труб и режима движения.
Для стальных труб при ламинарном движении используется формула:
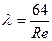
При турбулентном движении:
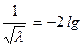
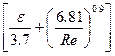
где ε - относительная шероховатость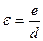 
,
е - абсолютная шероховатость, равная средней высоте выступов на поверхности трубы, м.
Более удобно для определения λ использовать график Никурадзе.
В тех случаях если сечение трубы или аппарата отличается от круглого, то вместо d используется величина эквивалентного диаметра: dэ =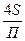 
S - площадь сечения, м2; П – смоченный периметр.
К местным сопротивлениям относится запорная арматура (вентили, краны, задвижки, отводы рис , колено ╗, двойники, тройники ╠ , крестоины ╬, диафрагмы рис , внезапные сужения, внезапные расширения и т.д.)
Потеря напора и перепад давления на преодоление местных сопротивлений рассчитывается по формулам:
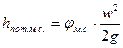
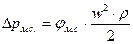
где φм.с. (дзетта) – коэффициент местного сопротивления.
Общие потери напора и перепад давления определяется по формулам
