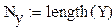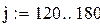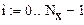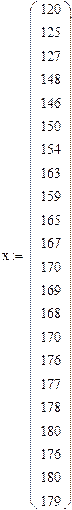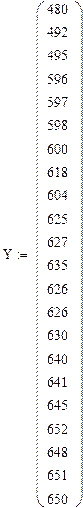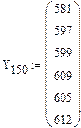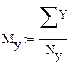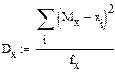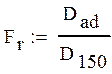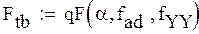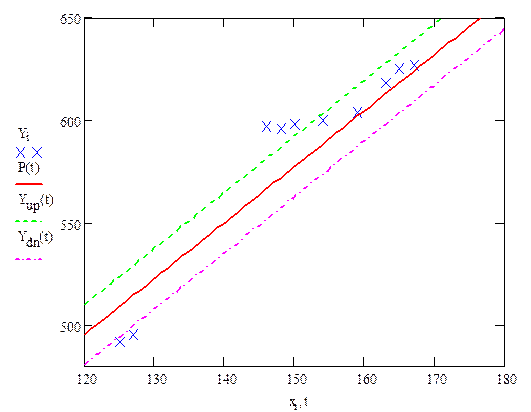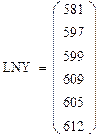7 . Расчет моментов распределения
1.Введение
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).
Mathcad имеет простой и интуитивный для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Некоторые из математических возможностей Mathcad (версии до 13.1 включительно) основаны на подмножестве системы компьютерной алгебры Maple . Начиная с 14 версии — использует символьное ядро MuPAD.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов [4]. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения
2.Описание МНК (метод наименьших квадратов)
Метод наименьших квадратов - один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины.
В этом общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки.
Рассмотрим рис. 1, отражающий большой разброс точек. В простейшем случае будем искать аппроксимирующую функцию ф(х) в виде полинома первой степени (прямой):
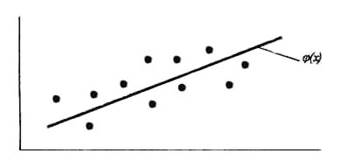
Рис. 2. График аппроксимации
Таким образом, данная система точек группируется вокруг искомой прямой. Эту прямую легко провести на глаз так, чтобы она наиболее близко подходила к исходным точкам. Однако можно найти уравнение прямой более строгими математическими методами.
Метод наименьших квадратов наиболее часто используют для решения контрольных по эконометрике для нахождения параметров уравнений (линий, степенной функции, гиперболы и т.д.)
Пусть общее количество точек равно n. Отклонение i-й точки от искомой прямой:
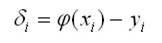
видно из рис. 2, отклонения могут быть как положительными, так и отрицательными. Поэтому для того, чтобы определить близость искомой функции к табличным точкам, необходимо составить сумму квадратов всех отклонений.
Метод наименьших квадратов заключается в минимизации суммы квадратов отклонений. В нашем случае эта функция равна
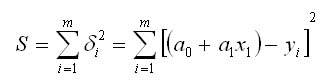
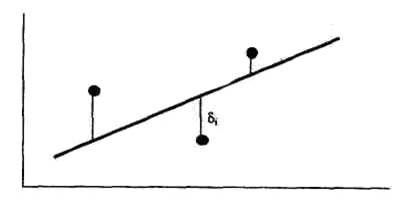
Рис. 2. График отклонения
Для нахождения минимума функции S необходимо приравнять нулю ее частные производные. В результате получим систему уравнений:
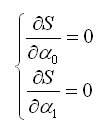
Опуская промежуточные преобразования, получим систему уравнений для нахождения неизвестных коэффициентов:
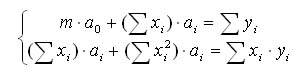
Здесь m - количество точек; суммирование здесь и далее предполагается по всем точкам.
Метод наименьших квадратов несложно распространить на общий случай, когда мы будем искать функцию ф(х) в виде полинома степени n:
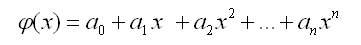
Отметим, что в случае аппроксимации всегда справедливо следующее соотношение, связывающее количество исходных точек m и степень искомого полинома:
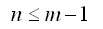
причем в случае равенства мы приходим к интерполяции (все отклонения равны нулю).
Неизвестные коэффициенты, а находим из условия минимизации суммы квадратов отклонений искомой функции от исходных точек. По аналогии с полиномом первой степени в нашем случае имеем систему уравнений: Z*A = B где Z - квадратная матрица размерностью (n+1)х(n+1), составленная из известных координат точек, А - вектор неизвестных коэффициентов; Y- вектор-столбец свободных членов.
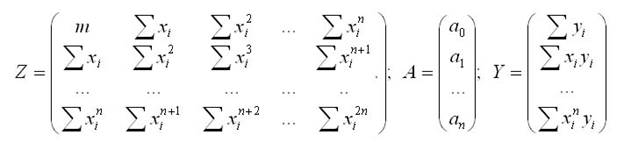
3.Постановка задачи
Для полного массива исходных данных с помощью персонального компьютера в системе MathCAD:
1) Провести сплайн – интерполяцию и построить гладкую интерполяционную кривую
2) Провести регрессионный анализ выборки и получить уравнение линейной регрессии . Построить линию регрессии.
3) Провести корреляционный анализ и определить коэффициент парной корреляции.
4) Оценить адекватность полученного уравнения регрессии , используя критерий Фишера для заданного уровня значимости
5) С помощью критерия Стьюдента оценить доверительный интервал для оценки истинных значений коэффициента корреляции и коэффициента регрессии. Расчеты выполнять для заданной доверительной вероятности.
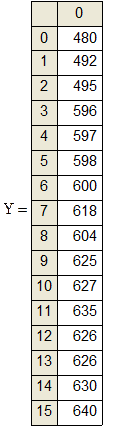
3.1 Экспериментальные данные
X: 120 125 127 148 146 150 154 163 159 165 167 170 169 168 170 176 177 178
180 176 180 179
Y: 480 492 495 596 597 598 600 618 604 625 627 635 626 626 630 640 641 645
652 648 651 650
Уровень значимости 0,05
Доверительная вероятность 0,9
3.2 Данные проверки точности X=150
Y: 581 597 599 609 605 612
3.3 Форма уравнения
Y= a0+a1x
4. Преобразование данных в МНК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

5. Расчет коэффициентов регрессии
|
|
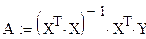
|
|
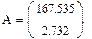
6. Построение графика линейных аргументов и точек эксперимента
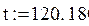
|
|
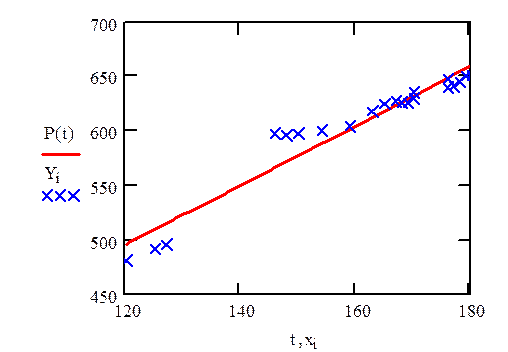
7 . Расчет моментов распределения
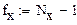
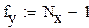
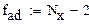
Расчет математических ожиданий
|
|
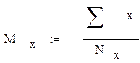
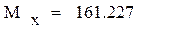
|
|
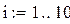
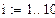
|
|
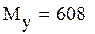
8. Расчет дисперсий
|
|
|
|
|
|
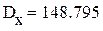
|
|
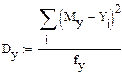
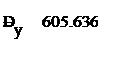
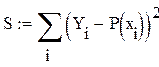
|
|
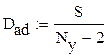
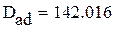
|
|
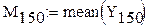
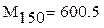
|
|
|
|
|
|
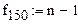
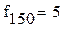
|
|
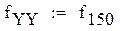
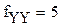
|
|
|
|
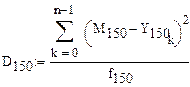
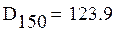
9.Оцениваем однородность дисперсий по критерию Фишера для доверительной вероятности 10% с помощью функции qF
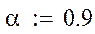
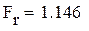
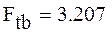
Табличное значение меньше расчетного, следовательно дисперсии неоднородны, модель адекватно описывает экспериментальные данные.
Оцениваем доверительный интервал расчетных значений по критерию Стьюдента с помощью функции qt
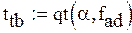
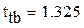
|
|
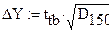
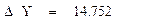
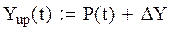
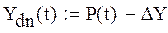
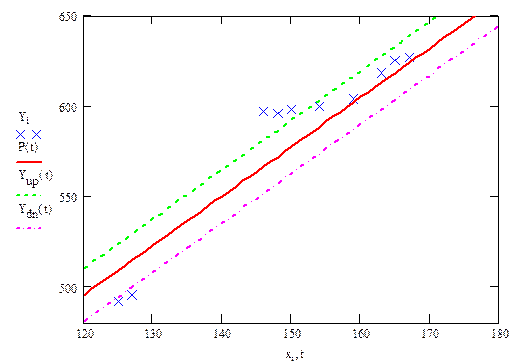
10. Строим график по полученным данным
|
|
|
|
11. Оцениваем коэффициент корреляции между X и Y по формуле
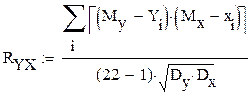 или используя функцию corr RRYX:=corr(Y,T)
или используя функцию corr RRYX:=corr(Y,T)
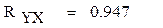
|
|
Коэффициент корреляции приближается к единице , следовательно связь между Y и X велика и функциональная зависимость между ними существует .
12. Оцениваем доверительные интервалы коэффициентов линейной модели с помощью матрицы дисперсий-ковариаций
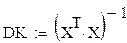
|
|
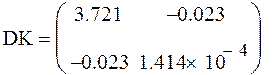
|
|
|
|
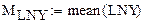
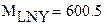
|
|
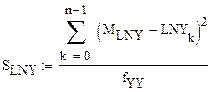
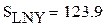
|
|
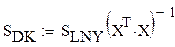
|
|
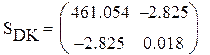
|
|
|
|
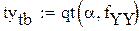
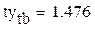
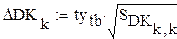
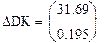
Доверительные интервалы значительно меньше соответствующих значений коэффициентов в матрице А , следовательно коэффициенты значимы.
13.Заключение
Табличное значение меньше расчетного, следовательно дисперсии неоднородны, модель адекватно описывает экспериментальные данные.
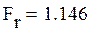
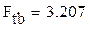
Коэффициент корреляции приближается к единице , следовательно связь между Y и X велика и функциональная зависимость между ними существует
RYX=0.947
Доверительные интервалы значительно меньше соответствующих значений коэффициентов в матрице А , следовательно коэффициенты значимы.
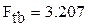
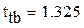
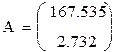
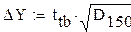
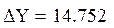
Уравнение соответствует, точки выпавшие за доверительный интервал считаем ошибочными данными:
|
|