Номер варианта – по списку в группе.
Задание №1
Номер варианта – по списку в группе.
Решить графическим методом задачу.
Из трех сортов бензина образуются две смеси. Первая состоит из А1 % бензина первого сорта, В1 % бензина 2-го сорта, С1 % бензина 3-го сорта; вторая: А2 % – 1-го, В2 % – 2-го, С2 % – 3-го сорта. Цена 1-й смеси – 305 у.е., второй – 200 у.е. за тонну. Сколько смеси первого и второго вида можно изготовить из “а” тонн 1-го сорта, “b” тонн 2-го сорта и “с” тонн 3-го сорта, чтобы получить максимальный доход?
| № задач | А1 | В1 | С1 | А2 | В2 | С2 | а | в | с |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 80 70 70 60 60 60 60 60 70 70 50 60 50 50 40 45 45 50 50 60 45 40 40 50 60 | 10 20 10 20 10 30 - 40 30 - 10 20 10 15 20 30 25 - 15 20 - 30 40 10 10 | 10 10 20 20 30 10 40 - - 30 40 20 40 35 40 25 30 50 35 20 55 30 20 40 30 | 20 20 30 30 30 30 10 20 10 20 10 20 25 30 35 40 45 50 55 10 15 20 25 30 35 | 30 40 40 20 50 30 80 10 60 60 20 40 45 35 30 45 10 15 - 20 25 30 35 40 45 | 50 40 30 50 20 40 10 70 30 20 70 40 30 35 35 5 45 35 45 70 60 50 40 30 20 | 16 28 26 24 39 27 18 24 14 28 14 16 18 22 24 26 28 30 36 38 40 42 44 46 48 | 13 32 18 10 20 15 48 14 45 42 45 40 35 30 25 20 15 55 50 45 40 35 30 25 20 | 21 30 16 16 21 8 14 42 21 20 21 18 27 24 21 27 30 33 21 27 18 15 21 27 30 |
Задание №2
Номер варианта – по списку в группе.
Симплекс методом решить ЗЛП.
Предприятие производит 3 вида продукции: А1, А2, А3, используя сырье двух видов: В1 и В2. Известны затраты сырья i-го вида на единицу изделия j-го вида аij , количество сырья каждого вида bi (i = 1, 2), а также прибыль, полученная от единицы изделия j-го вида сj (j = 1, 2, 3).
Сколько изделий каждого вида необходимо произвести, чтобы получить 1) максимум прибыли;
2) максимум товарной продукции?
Обозначения: в таблице приведена матрица затрат: А = (аij), справа от таблицы значение bi (i = 1, 2) и внизу сj (j = 1, 2, 3).
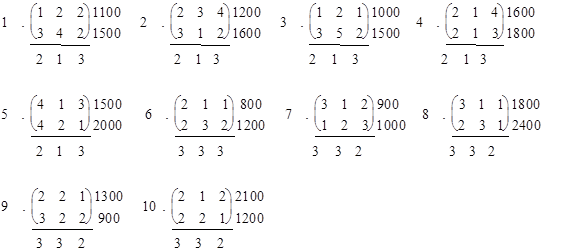
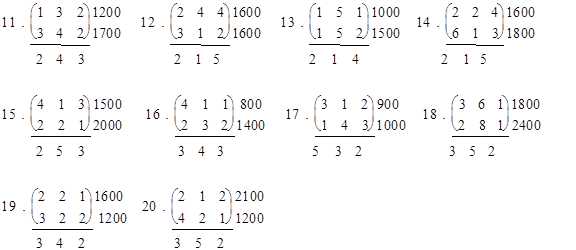
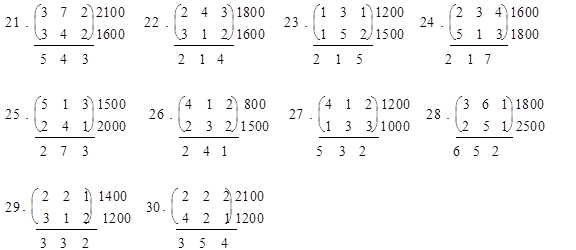
Задание №3
Решение задач линейного программирования двойственным симплекс-методом ( P – методом).








