5.8. Перевірка адекватності тренду моделі об'єкту

Дата: 2025-05-01; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Не залежно від вигляду способу побудови моделі, питання про можливість її застосування з метою аналізу й прогнозування явища може бути вирішено тільки після встановлення адекватності, тобто відповідності моделі досліджуваному процесу або об'єкту. Трендова модель 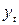конкретного часового ряду 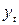вважається адекватною, якщо правильно відбиває систематичні компоненти часового ряду. Ця вимога еквівалентно вимозі, щоб залишковий компонент 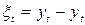задовольняв властивостям випадкового компонента часового ряду:

1. випадковість коливань рівнів залишкової послідовності;

2. відповідність розподілу випадкового компонента нормальному закону розподілу;

3. рівність математичного очікування випадкового компонента нулю;

4. незалежність значень рівнів випадкового компонента.

 

5.8.1. Перевірка випадковості коливань рівнів залишкової послідовності

 

Означає перевірку гіпотези про правильність вибору виду тренда. Для дослідження випадковості відхилень від тренда ми маємо у своєму розпорядженні набір різниць:

 

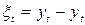(t=1,2,…,n).

 

Характер цих відхилень вивчається за допомогою ряду непараметричних критеріїв. Одним з таких критеріїв є критерій серій, заснований на медіані вибірки. Ряд з величин розташовують у порядку зростання їхніх значень і знаходять медіану 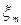отриманого варіаційного ряду, тобто серединне значення при непарному n або середню арифметичну із двох серединних значень при n парному. Вертаючись до вихідної послідовності 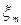й порівнюючи значення цієї послідовності з 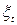, будемо ставити знак "плюс", якщо значення 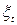перевершує медіану, і знак "мінус", якщо воно менше медіани; у випадку рівності порівнюваних величин відповідне значення 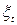опускається. Таким чином, виходить послідовність, що складається із плюсів і мінусів, загальне число яких не перевершує n. Послідовність підряд, що йдуть плюсів, або мінусів називається серією. Для того щоб послідовність 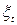була випадковою вибіркою, довжина самої довгої серії не повинна бути занадто великий, а загальне число серій − занадто малим.

Позначимо довжину самої довгої серії через Кмах, а загальне число серій − через v. Вибірка зізнається випадкової, якщо виконуються наступні нерівності для 5%-ного рівня значимості:

 

 

 

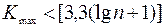
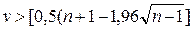
де квадратні дужки, як звичайно, означають цілу частину числа.

Якщо хоча б одна з нерівностей не виконується, то гіпотеза о випадковім характері відхилень відкидається і модель вважається не адекватною.

Іншим критерієм для даної перевірки може служити критерій піків (поворотних крапок). Рівень послідовності е( уважається максимумом, якщо він більше двох рядом вартих рівнів, Т.ч. 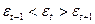, і мінімумом, якщо він менше обох сусідніх рівнів, тобто 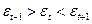. В обох випадках уважається поворотною точкою; загальне число поворотних точок для залишкової послідовності позначимо через р.

У випадковій вибірці математичне очікування числа крапок повороту 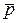і дисперсія σ2р виражаються формулами:

 

;

 

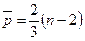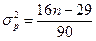
Критерієм випадковості з 5%-ним рівнем значимості, тобто з довірчою ймовірністю 95%, є виконання нерівності

,

 

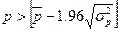де квадратні дужки, як і раніше, означають цілу частину числа.

Якщо нерівність не виконується, модель вважається не адекватною.

 

5.8.2. Перевірка відповідності розподілу випадкового компонента нормальному закону розподілу

 

Може бути зроблена лише приблизно за допомогою дослідження показників асиметрії ( 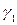) і ексцесу ( 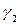),тому що тимчасові ряди, як правило, не дуже великі. При нормальному розподілі показники асиметрії й ексцесу деякої генеральної сукупності дорівнюють нулю. Ми припускаємо, що відхилення від тренда являють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії й ексцесу і їхньої помилки:

 

 

;  
;  
;  
;  

 

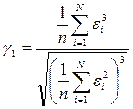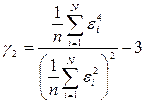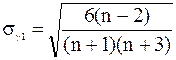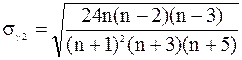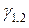− вибірна характеристика асиметрії, ексцесу;

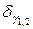− середньоквадратичні помилки.

 

 

Якщо одночасно виконуються наступні нерівності:

 

 

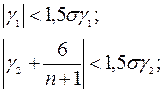
то гіпотеза о нормальнім характері розподілу випадкової компоненти приймається.

Якщо виконується хоча б одне з нерівностей:

 

 

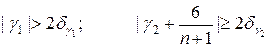
то гіпотеза відкидається та модель вважається неадекватною.

 

5.8.3. Перевірка рівності математичного очікування випадкового компонента нулю

Якщо вона розподілена за нормальним законом, здійснюється на основі t-критерію Стьюдента. Розрахункове значення цього критерію задається формулою:

 

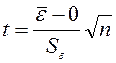
Якщо розрахункове значення t менше табличного значення tа статистики Стьюдента із заданим рівнем значимості а й числом ступенів волі n-1, то гіпотеза про рівність нулю математичного очікування випадкової послідовності приймається; у противному випадку ця гіпотеза відкидається й модель уважається неадекватною.

 

5.8.4. Перевірка незалежності значень рівнів випадкового компонента.

Т.ч. перевірка відсутності істотної автокореляції в залишковій послідовності може здійснюватися по ряду критеріїв, найпоширенішим з яких є d- критерій Дарбина-Уотсона. Розрахункове значення цього критерію визначається по формулі:

 

 

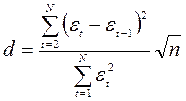
Помітимо, що розрахункове значення критерію Дарбина- Уотсона в інтервалі від 2 до 4 свідчить про негативний зв'язок; у цьому випадку його треба перетворити по формулі d' = 4 - d і в подальшому використовувати значення d'.

Розрахункове значення критерію d (або d') рівняється з верхнім d2 і нижнім d1 критичними значеннями статистики Дарбина-Уотсона, фрагмент табличних значень яких для різного числа рівнів ряду п і числа обумовлених параметрів моделі.

 

Таблица

d-критерий Дарбина-Уотсона

n

k=1

k=2

k=3
d1 d2 d1 d2 d1 d2
15 20 30 1,08 1,20 1,35 1,36 1.41 1,49 0,95 1,10 1,28 1,54 1,54 1,57 0,82 1,00 1,21 1,75 1,68 1,65

 

 

Висновок про адекватність трендової моделі робиться, якщо всі зазначені вище чотири перевірки властивостей залишкової послідовності дають позитивний результат. Для адекватних моделей має сенс ставити завдання оцінки їхньої точності. Точність моделі характеризується величиною відхилення виходу моделі від реального значення моделюючої змінної (показника). Для показника, представленого часовим рядом, точність визначається як різниця між значенням фактичного рівня тимчасового ряду і його оцінкою, отриманої розрахунковим шляхом з використанням моделі, при цьому як статистичні показники точності застосовуються наступні:

Середнє квадратичне відхилення:

 

 

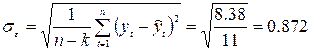
Середня відносна помилка апроксимації:

 

 

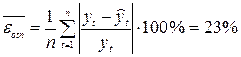
Коефіцієнт збіжності:

 

 

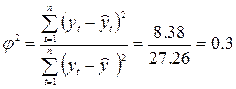
Коефіцієнт детермінації:

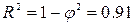
5.9. Рекомендації по виконанню на ЕОМ

Виконання курсової роботи вимагає значних по об'єму розрахунків. Проводити їх необхідно на ЕОМ. Рекомендується використовувати для розрахунків пакет програм "Маtсаd 2000", або аналогічні програми. Для оформлення розрахунків рекомендується пакет програм "Word 2000". Додаткове індивідуальне завдання передбачає самостійно складену програму. Програма приводитися в доповненні до КР. Виконання курсової роботи задовільно підготовленим студентом вимагає 20-30 години машинного часу.