5.4. Вибір моделі об'єкта дослідження.
Планування експерименту базується на кібернетичних поданнях про об'єкт досліджень. У зв'язку із цим, при новому підході до проведення експерименту в якості найбільше підходящої моделі об'єкта досліджень рекомендується вибирати так званий чорний ящик (Рис. 5.1).
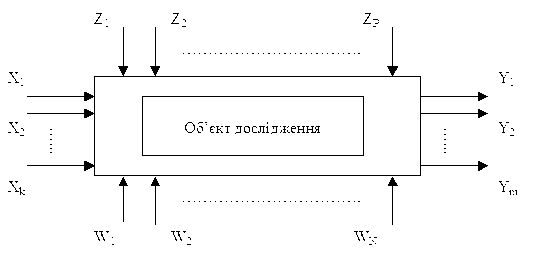
Рис.5.1. Модель об'єкта досліджень
Принципи побудови такої моделі звичайно відповідають апріорним поданням експериментатора про об'єкт дослідженні при рішенні в умовах неповного знання механізму явищ складних багатофакторних задач.
До числа вхідних параметрів об'єкта дослідження відносять керуючі, контрольовані й параметри, що обурюють. Керуючі параметри (або фактори) Х1, Х2, ... , Хk − основні, на них можна впливати з метою зміни стану об'єкта (зміни вихідних параметрів об'єкта).
Контрольовані параметри Z1, Z2, ... , ZР вимірюють у процесі дослідження, їх не змінюють цілеспрямовано (звичайно можливість впливу на них відсутній).
Параметри, що збурюють (W1, W2…,WN) − неконтрольовані, вони недоступні для виміру, їхні значення змінюються в часі випадковим образом.
Застосовувані моделі в загальному виді мають форму рівнянь виду:
.
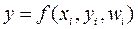де f − функція, що задає співвідношення між Xi, Zi і Wi.
Метою експерименту є вивчення залежності між вихідними параметрами й факторами, тому модель об'єкта дослідження шукається у вигляді рівняння:
.
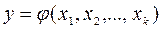Звичайно вище наведена залежність шукається у вигляді поліномінального рівняння, тобто:
.
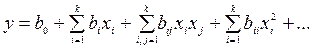По величині коефіцієнтів полінома (коефіцієнтів регресії) судять про ефекти або про ступінь впливу відповідних факторів на величину Y.
Ступінь полінома підвищують у кілька послідовних етапів, після того, як доведена необхідність цього на попередніх стадіях дослідження.
На першому етапі модель об'єкта шукається у вигляді полінома першого порядку, що містить вільний член, члени з лінійними ефектами й члени з ефектами взаємодії всіх порядків.
Так, у даній курсовій роботі для k = 4 така модель буде мати вигляд:
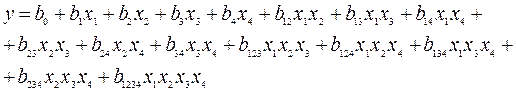
Число лінійних коефіцієнтів рівняння регресії знайти легко: воно дорівнює числу факторів, що враховують відповідною матрицею ПФЭ.
5.5. Розрахунки коефіцієнтів регресії
Лінійні коефіцієнти регресії розраховують по формулі:
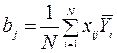
де хij − значення фактору X в i-му досвіді;
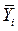− середнє значення вихідного параметра в тім же досвіді;
N − число досвідів у матриці.
При визначенні вільного члена в рівнянні регресії (b0) беруть середнє арифметичне всіх значень вихідного параметра:
.
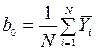Коефіцієнти регресії, що характеризують парний вплив факторів, знаходять по формулі:
.
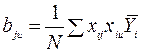Розраховуємо лінійні коефіцієнти регресії:
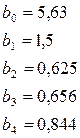
Таким чином, рівняння регресії приймає вид:
.
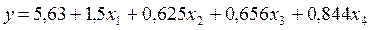Після визначення коефіцієнтів лінійної моделі оцінюємо їхню значимість і перевіряємо адекватність моделі досліджуваному об'єкту.
5.6. Перевірка значимості коефіцієнтів регресії
Знання дисперсії відтворюваності дає можливість оцінити значимість коефіцієнтів рівняння регресії. Наявність інформації про значимості коефіцієнтів дозволяє розглянути питання про можливості спрощення наступної роботи шляхом відсівання частини факторів. Крім того, така інформація полегшує інтерпретацію математичних моделей об'єктів дослідження.
Значимість коефіцієнтів рівняння регресії можна оцінити за допомогою критерію Стьюдента:
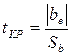
де be − модуль е-того коефіцієнта рівняння регресії;
Sb − середньоквадратичне відхилення значень коефіцієнтів рівняння регресії.
Величину Sb знаходять через дисперсію відтворюваності Sy2 за допомогою виразів:
,
,
.
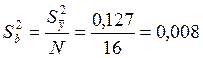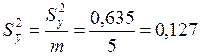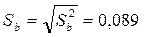Значимість коефіцієнтів рівняння регресії визначають порівнянням табличного значення t-критерію з розрахунковим. Якщо для даного коефіцієнта bг розрахункове значення критерію Стьюдента менше табличного значення (tе расч. < t табл.), то такий коефіцієнт є статистично незначущим і його можна виключити з подальшого розгляду моделі.
Табличне значення t-критерію, як і раніше, можуть бути знайдені з додатка 1. Число ступенів волі, прийняте в увагу при виборі tтабл., уважають рівним тому числу ступенів волі, що використалося при оцінці припустимого відхилення величини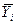 
.
Перевіряємо виконання нерівність:
.
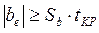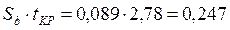
Тому що знайдені лінійні коефіцієнти регресійного рівняння більше заданого значення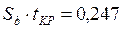 
, отже, всі ці коефіцієнти є значимими й впливають на вихідну величину.
5.7. Перевірка адекватності моделі об'єкту
Гіпотезу про адекватність (відповідності) моделі досліджуваному об'єкту перевіряють за допомогою критерію Фишера:
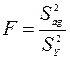
| (5.1) |
де Sag − дисперсія адекватності.
Щоб знайти дисперсію адекватності потрібно для кожного i-го досвіду обчислити за допомогою рівняння регресії значення вихідного параметра.
У даній курсовій роботі рівняння регресії має вигляд:
.
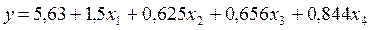Розрахункові значення вихідного параметра наведені в табл. 5.4.
Таблиця 5.4
| № | Рівень факторів | Лінійні коефіцієнти | YPi | ||||||||
| Х0 | Х1 | Х2 | Х3 | Х4 | b0 | b1 | b2 | b3 | b4 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 5,63 | 1,5 | 0,625 | 0,656 | 0,844 | 9,25 |
| 2 | 1 | -1 | 1 | 1 | 1 | 6,25 | |||||
| 3 | 1 | 1 | -1 | 1 | 1 | 8 | |||||
| 4 | 1 | -1 | -1 | 1 | 1 | 5 | |||||
| 5 | 1 | 1 | 1 | -1 | 1 | 7,938 | |||||
| 6 | 1 | -1 | 1 | -1 | 1 | 4,938 | |||||
| 7 | 1 | 1 | -1 | -1 | 1 | 6,688 | |||||
| 8 | 1 | -1 | -1 | -1 | 1 | 3,688 | |||||
| 9 | 1 | 1 | 1 | 1 | -1 | 7,563 | |||||
| 10 | 1 | -1 | 1 | 1 | -1 | 4,563 | |||||
| 11 | 1 | 1 | -1 | 1 | -1 | 6,313 | |||||
| 12 | 1 | -1 | -1 | 1 | -1 | 3,313 | |||||
| 13 | 1 | 1 | 1 | -1 | -1 | 6,25 | |||||
| 14 | 1 | -1 | 1 | -1 | -1 | 3,25 | |||||
| 15 | 1 | 1 | -1 | -1 | -1 | 5 | |||||
| 16 | 1 | -1 | -1 | -1 | -1 | 2 | |||||
Дисперсія адекватності знаходиться з виразу:
,
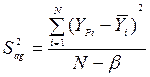де b − число коефіцієнтів регресії.
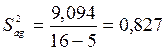
Значення F-критерію, знайдене з рівняння (5.1), порівнюють із табличним Fтабл., обраним для відповідної довірчої ймовірності й з урахуванням числа ступенів волі для більшої (r1) і меншої (r2) дисперсією. У цьому випадку:
r1=N- b =11
r2=N=16
Якщо Fрасч. < Fтабл., те гіпотеза про адекватність моделі об'єкту приймається. Якщо ж Fрасч. > Fтабл., те модель неадекватна об'єкту й рекомендується проведення додаткового експерименту для уточнення моделі.
У даній курсовій роботі:
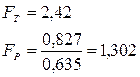
Таким чином,
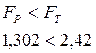
Отже, обрана модель адекватна об'єкту.