3. Структура й зміст курсової роботи
Зміст основних розділів КР визначається завданням на проектування. Завдання видається кожному студентові на першому консультаційному занятті. Оформлення студентом бланка завдання на КР є для викладача інформацією про те, що студент приступив до виконання КР.
Курсова робота складається з текстової (розрахункової) частини.
Зміст текстової частини може бути наступній:
Титульний аркуш (см. додаток А).
Завдання на курсову роботу.
Реферат.
Зміст.
Вступ.
1. Планування експерименту для розв’язання задач ідентифікації.
1.1 . Вибір факторів і їх нормалізування.
1.2 . Побудова і аналіз плану ПФЕ.
1.3 . Статистичний аналіз результатів експерименту.
2. Математична модель об’єкта.
2.1 . Розрахунок коефіцієнтів математичної моделі.
2.2 . Перевірка значимості коефіцієнтів регресії.
3. Перевірка адекватності моделі об’єкту.
4. Уточнення моделі.
Висновок.
Список використаних джерел.
Додатки (при необхідності).
У залежності від конкретного варіанта завдання в текстову частину можуть бути введені додаткові розділи або деякі можуть бути виключені з даного переліку. Структура і зміст КР визначається викладачем. Обсяг текстової частини – 30...40 аркушів формату А4, написаних від руки або роздрукованих на принтері.
4. ВКАЗІВКИ щодо виконання курсової роботи
При виконанні КР необхідно послідовно розробляти основні розділи, використовуючи літературу, що рекомендується, і дані методичні вказівки.
В вступі варто відобразити застосування теорії ідентифікації в різних галузях виробництва й інших сфер людської діяльності; указати мета й основні задачі КР.
У розділі «Планування експерименту для розв’язання задач ідентифікації» необхідно проаналізувати фактори, розрахувати нульову точку експерименту, скласти план повного факторного експерименту і проаналізувати його властивості (ортогональність, симетричність і нормірованість). А також провести статистичний аналіз результатів експерименту для підтвердження відтворюваності досвідів, що виконується за допомогою аналізу оцінок дисперсії за критерієм Кохрена.
У розділі «Математична модель об’єкта» необхідно визначити залежності між вихідними параметрами й факторами, тому модель об'єкта дослідження шукається у вигляді рівняння:
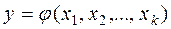
| (4.1) |
Звичайно залежність (4.1) шукається у вигляді поліноміального рівняння, тобто
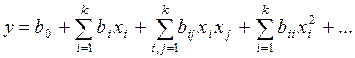
| (4.2) |
По величині коефіцієнтів полінома (коефіцієнтів регресії) судять про ефекти або про ступінь впливу відповідних факторів на величину y.
Ступінь полінома підвищують у кілька послідовних етапів, після того, як доведена необхідність цього на попередніх стадіях дослідження.
Коефіцієнти лінійної регресії розраховують за методом найменших квадратів. Значимість коефіцієнтів регресії оцінюється за допомогою критерію Стьюдента:
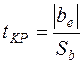
де be – модуль е-того коефіцієнта рівняння регресії;
Sb – средньоквадратичне відхилення значень коефіцієнтів рівняння регресії,
t КР – значення критерію Стьюдента з необхідною достовірністю.
У розділі «Перевірка адекватності моделі об'єкту» гіпотезу про адекватність (відповідність) моделі досліджуваному об'єкту перевіряють за допомогою критерію Фишера:
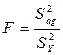
де Sag – дисперсія адекватності.
Щоб знайти дисперсію адекватності потрібно для кожного i-го досвіду обчислити за допомогою рівняння регресії значення вихідного параметра.
Висновок повинний містити висновки й оцінку отриманих результатів у цілому, з погляду відповідності їхньому завданню, порівняння результатів розрахунків, проведених у різних розділах КР.
У додатках містяться тексти програм для ЕОМ, які були написані й використані при виконанні КР, а також роздруківки з результатами виконання цих програм; блок схеми систем (якщо смороду не були поміщені в тексті пояснювальної записки).
Літературні джерела, використані при виконанні КР, заносяться в список. Джерела в списку варто розташовувати у відповідності з посиланнями на них. Список оформляється як розділ КР відповідно до вимог ДЕРЖСТАНДАРТ 7.1-84.
5. Рекомендації щодо виконання курсової роботи
Дисципліна «Методи ідентифікації систем керування» тісно пов'язана з іншими дисциплінами, такими як: «Спеціальні розділи математики», «Теорія автоматичного керування» «Оптимальне й адаптивне керування» і ін. Знання, які отримані із цих дисциплін, будуть використані при роботі над курсовою роботою по дисципліні МИСУ. У першу чергу потрібні знання по роботі з матрицями, по обробці статистичного матеріалу по програмуванню.
Необхідно скласти план повного факторіального експерименту, виконати статистичний аналіз результатів експерименту досліджуваного об'єкта, перевірити значимість коефіцієнтів моделі й оцінити адекватність побудованої моделі об'єкту. При роботі над матеріалом рекомендується використати ЕОМ. У даній курсовій роботі заданий об'єкт досліджень, основні фактори, що впливають на нього, діапазони зміни, вихідний параметр об'єкта й результати його виміру в ході повного факторного експерименту над об'єктом.
5.1. Вибір факторів рівнів їхнього варіювання й нульової точки
Фактором називається керована незалежна змінна, що впливає на об'єкт дослідження. Фактор уважається заданим, якщо вказані його назва й область визначення. Обрані для експерименту кількісні або якісні стани факторів звуться рівнів фактору. При плануванні експерименту значення факторів, що відповідають певним рівням їхнього варіювання, виражають у кодованих величинах.
Під інтервалом варіювання фактору мається на увазі різниця між двома його значеннями, прийнята за одиницю при кодуванні, від руки або в друкованому виді.
Як фактори доцільно вибирати такі незалежні змінні, які відповідають одному з розумних, у розглянутому випадку, впливів на об'єкт досліджень, які можуть бути виміряни наявними засобами з досить високою точністю і є керованими, однозначними й сумісними один з іншим. Вимога керованості пов'язано з необхідністю забезпечення в ході експерименту декількох рівнів варіювання кожного фактору, причому в окремому досвіді обраний рівень варіювання повинен підтримуватися досить точно.
При виборі області визначення факторів рекомендується звертати спеціальну увагу на вибір нульової крапки. Вибір нульової точки еквівалентний визначенню такого стану об'єкта дослідження, що приймається за вихідне. Часто при постановці задачі область визначення факторів буває заданої. Тоді центр цієї області приймається за нульову крапку.
Після встановлення нульових точок вибирають інтервали варіювання факторів у кодованих величинах. Вони відповідають значенням +1 і -1. Вибір факторів завершується складанням списку всіх факторів із вказівкою найменування й позначення факторів, їхніх інтервалів варіювання й координат нульової точки. Всі ці дані зводяться в таблицю.
Таблиця 5.1.
| Найменування й позначення факторів | Рівні варіювання | Інтервал варіювання | ||
| -1 | 0 | +1 | ||
| Відстань до об'єкта, м (Х1) | 10 | 55 | 100 | 45 |
| Кількість команд (Х2) | 5 | 15 | 25 | 10 |
| Частота проходження сигналів, кгц (Х3) | 1 | 50,5 | 100 | 49,5 |
| Амплітуда дискретного сигналу, В (Х4) | 2 | 6 | 10 | 4 |
За нульову точку приймаємо значення даного фактору, що відповідає середньому значенню даного фактору:
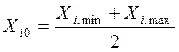
Після встановлення нульових точок вибираємо інтервали варіювання факторів у кодованих величинах +1 і -1:
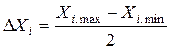
5.2. Складання плану повного факторного експерименту
Повний факторний експеримент (ПФЭ) − це експеримент, у якому реалізуються всі можливі комбінації розглянутих рівнів факторів, а результати оцінюються за допомогою статистичного аналізу. Число досвідів у повному факторному експерименті визначається зі співвідношення:
N=Pk ,
де N – число досвідів;
Р = 2 – число рівнів варіювання факторів;
k = 4 – число факторів.
Це співвідношення справедливо для випадку, коли число рівнів для всіх факторів плану однаково. У випадку двухрівневого варіювання факторів (+1 і -1) число досвідів у ПФЭ дорівнює: N=2k = 24 = 16.
У плані ПФЭ (матриці планування) при варіюванні факторів на двох рівнях показують тільки знаки + або -.
У першому стовпці матриці планування вказують кодоване значення числа (b0) у рівнянні регресії. Число стовпців матриці дорівнює числу факторів, що враховують. Іноді додають стовпці, що відповідають взаємодіям факторів.
Число рядків визначається з умови N = 2k. В окремому стовпці вказують номера досвідів.
Повний факторний експеримент ставиться до числа планів, які є найбільш ефективними при побудові лінійних моделей.
Достоїнствами ПФЭ варто вважати ортогональність, рототабельність, симетричність щодо центра експерименту й відповідність рівню нормірування.
Планування називається ортогональним, якщо сума добутків двох будь-яких стовпців матриці дорівнює нулю, тобто:
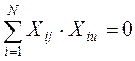при j ¹ u ,
де j, u =0,1,…, K;
K = 4 − число факторів (номер останнього стовпця плану);
N = 16 − число досвідів;
i − номер досвіду.
Ортогональність плану дозволяє одержувати оцінки для коефіцієнтів регресії незалежними друг від друга й дає можливість відкидати ті фактори, при яких коефіцієнти виявляються незначущими.
Умові симетричності плану щодо центра експерименту відповідає співвідношення:
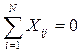при 
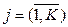
Умова нормірування плану виконується, якщо:
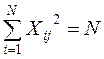при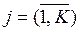 
При виконанні умов ортогональності, симетричності й нормірування плану коефіцієнти рівняння регресії оцінюються з мінімальною регресією.
5.3. Статичний аналіз результатів експерименту
Будь-який експеримент складається із групи досвідів, окремий досвід складається з декількох спостережень (повторень досвіду), а кожне спостереження − із серії повторних вимірів. Відповідно розрізняють помилку експерименту (помилку відтворюваності), помилки досвідів і помилки спостережень. Знання помилок досвідів і експерименту необхідно для правильного рішення задач, пов'язаних з оцінкою точності й надійності результатів роботи, визначенням значимості коефіцієнтів рівняння й перевіркою адекватності (придатності) одержуваних математичних моделей.
Розрізняють кілька видів помилок вимірів: грубі, систематичні й випадкові. Грубі помилки можливі через порушення основних умов виміру або у зв'язку з недоглядом дослідника, його неуважністю. Результат, що містить грубу помилку, називається промахом. При виявленні грубої помилки рекомендується відразу ж відкинути відповідний результат виміру.
Систематичні помилки викликаються впливом факторів, які проявляються однаково при багаторазовому повторенні тих самих вимірів. Після виявлення систематичних помилок (шляхом виміру, наприклад, різними приладами або різними методами тих самих величин) їх можна легко усунути шляхом введення необхідних виправлень.
При обробці результатів досліджень, пов'язаних із плануванням експерименту, уважають, що систематичні помилки попередньо усунуті й можуть мати місце лише промахи й випадкові помилки.
Передбачається, що розподіл результатів окремих спостережень підкоряється закону нормального розподілу; тому при обробці результатів експерименту визначають середнє арифметичне значення вихідного параметра Yi (i = 1, 2, ..., N) в окремому i-му досвіді й дисперсію помилки досвіду Si2 :
,
.
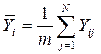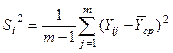Таблиця 5.2
| № | Рівень факторів | Вихідний параметр | Yi.cp | Si2 | ||||||||
| Х0 | Х1 | Х2 | Х3 | Х4 | Y1 | Y2 | Y3 | Y4 | Y5 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 7 | 8 | 9 | 9 | 6 | 7,8 | 1,7 |
| 2 | 1 | -1 | 1 | 1 | 1 | 6 | 7 | 7 | 5 | 6 | 6,2 | 0,7 |
| 3 | 1 | 1 | -1 | 1 | 1 | 7 | 8 | 9 | 10 | 7 | 8,2 | 1,7 |
| 4 | 1 | -1 | -1 | 1 | 1 | 5 | 6 | 5 | 4 | 5 | 5 | 0,5 |
| 5 | 1 | 1 | 1 | -1 | 1 | 8 | 9 | 10 | 7 | 6 | 8 | 2,5 |
| 6 | 1 | -1 | 1 | -1 | 1 | 4 | 5 | 3 | 6 | 7 | 5 | 2,5 |
| 7 | 1 | 1 | -1 | -1 | 1 | 9 | 8 | 7 | 9 | 6 | 7,8 | 1,7 |
| 8 | 1 | -1 | -1 | -1 | 1 | 3 | 4 | 3 | 2 | 5 | 3,4 | 1,3 |
| 9 | 1 | 1 | 1 | 1 | -1 | 9 | 8 | 7 | 6 | 8 | 7,6 | 1,3 |
| 10 | 1 | -1 | 1 | 1 | -1 | 5 | 6 | 8 | 4 | 4 | 5,4 | 2,8 |
| 11 | 1 | 1 | -1 | 1 | -1 | 7 | 6 | 5 | 6 | 7 | 6,2 | 0,7 |
| 12 | 1 | -1 | -1 | 1 | -1 | 4 | 3 | 2 | 4 | 3 | 3,2 | 0,7 |
| 13 | 1 | 1 | 1 | -1 | -1 | 8 | 7 | 7 | 6 | 5 | 6,6 | 1,3 |
| 14 | 1 | -1 | 1 | -1 | -1 | 1 | 3 | 2 | 3 | 2 | 2,2 | 0,7 |
| 15 | 1 | 1 | -1 | -1 | -1 | 5 | 3 | 3 | 4 | 3 | 3,6 | 0,8 |
| 16 | 1 | -1 | -1 | -1 | -1 | 2 | 3 | 4 | 2 | 5 | 3,2 | 1,7 |
Величина Si2 характеризує точність i-го досвіду. Припустимі відхилення величини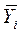 
від істинного значення вихідного параметра Y можна оцінити з обліком необхідної довірчої ймовірності (a), що характеризує надійність результатів досвідів. При цьому використається вираз:
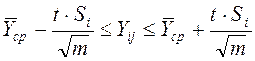
тут t − критерій Стьюдента.
Значення критерію Стьюдента при прийнятій довірчій імовірності a =0,95 і m=5 дорівнює: tКР=2,78.
Тому що є результати виміру Yij при i - м досвіді, що «вискакує» за межі довірчого інтервалу (9), те це промах і його можна виключити з результатів вимірів. Після цього середнє значення вихідного параметра (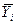 
) і дисперсія помилки (Si2) ці досвіди перераховується.
Таблиця 5.3
| № | Рівень факторів | Вихідний параметр | Yi.cp | Si2 | ||||||||
| Х0 | Х1 | Х2 | Х3 | Х4 | Y1 | Y2 | Y3 | Y4 | Y5 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 7 | 8 | 9 | 9 | 8,25 | 0,917 | |
| 2 | 1 | -1 | 1 | 1 | 1 | 6 | 7 | 7 | 6 | 6,5 | 0,333 | |
| 3 | 1 | 1 | -1 | 1 | 1 | 7 | 8 | 9 | 7 | 7,75 | 0,917 | |
| 4 | 1 | -1 | -1 | 1 | 1 | 5 | 5 | 5 | 5 | 0 | ||
| 5 | 1 | 1 | 1 | -1 | 1 | 8 | 9 | 7 | 8 | 1 | ||
| 6 | 1 | -1 | 1 | -1 | 1 | 4 | 5 | 6 | 5 | 1 | ||
| 7 | 1 | 1 | -1 | -1 | 1 | 9 | 8 | 7 | 9 | 8,25 | 0,917 | |
| 8 | 1 | -1 | -1 | -1 | 1 | 3 | 4 | 3 | 2 | 3 | 0,667 | |
| 9 | 1 | 1 | 1 | 1 | -1 | 9 | 8 | 7 | 8 | 8 | 0,667 | |
| 10 | 1 | -1 | 1 | 1 | -1 | 5 | 6 | 4 | 4 | 4,75 | 0,917 | |
| 11 | 1 | 1 | -1 | 1 | -1 | 7 | 6 | 6 | 7 | 6,5 | 0,333 | |
| 12 | 1 | -1 | -1 | 1 | -1 | 4 | 3 | 4 | 3 | 3,5 | 0,333 | |
| 13 | 1 | 1 | 1 | -1 | -1 | 8 | 7 | 7 | 6 | 7 | 0,667 | |
| 14 | 1 | -1 | 1 | -1 | -1 | 3 | 2 | 3 | 2 | 2,5 | 0,333 | |
| 15 | 1 | 1 | -1 | -1 | -1 | 3 | 3 | 4 | 3 | 3,25 | 0,25 | |
| 16 | 1 | -1 | -1 | -1 | -1 | 2 | 3 | 4 | 2 | 2,75 | 0,917 | |
Дисперсії досвідів Si2 повинні бути однорідними. Це − вимога наступного регресійного аналізу.
Однорідність дисперсій досвідів перевіряється за допомогою критерію Кохрена (G), що дорівнює відношенню максимальної дисперсії досвіду Si2max до суми всіх дисперсій:
.
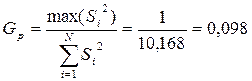Дисперсії досвідів можна вважати однорідними, якщо розрахункове значення критерію Кохрена (Gр.) менше табличного (Gт). Табличні значення критерію наведені в додатку Л і вони відносяться до довірчої ймовірності 0,95, числу досвідів N=16 і значенню числа ступеня волі f = m - 1=5-1=4.
Знаходимо: GТ = 0,229.
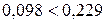тобто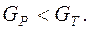 
Отже, дисперсії досвідів є однорідними.
Однорідність дисперсій досвідів можна оцінити й за критерієм Фишера (F). У цьому випадку із загального числа дисперсій досвідів беруть тільки дві − максимальну й мінімальну. Критерій Фишера є відношення максимальної дисперсії до мінімальної:
.
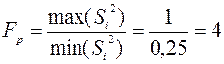Якщо розрахункове значення критерію Фишера (Fрасч.) менше табличного (F табл.), то дисперсії досвідів однорідні. Табличні значення критерію Фишера при довірчій імовірності 0,95 дані в додатку 3 [1].
При r1 = r2 = m -1 = 4 табличний критерій Фишера дорівнює: FT = 6,39.
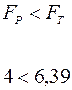
Таким чином, за критерієм Фишера дисперсії досвідів також є однорідними.
Однорідність дисперсій досвідів дає можливість переходити до оцінки дисперсії експерименту в цілому – SY2 (дисперсії відтворюваності), що характеризує помилку всього експерименту. Знання цієї дисперсії необхідно для наступного регресійного аналізу.
Дисперсія відтворюваності може бути знайдена за допомогою вираження:
.
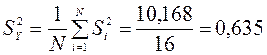