1.53. Окружная скорость рабочего колеса на диаметре .
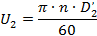
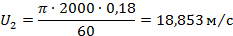
1.54.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 15 |
| КР ЛГМ и ГДП |
Меридиональная составляющая абсолютной скорости потока на выходе колеса (из уравнения неразрывности) с учетом стеснения потока лопатками:
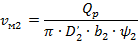
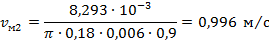
1.55. Окружная составляющая абсолютной скорости потока на выходе колеса для бесконечного числа лопастей (из треугольника скоростей) [1]:
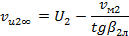
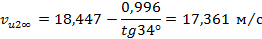
1.56. Окружная составляющая абсолютной скорости потока на выходе колеса для конечного числа лопастей при отсутствии закрутки на входе в рабочее колесо (из основного уравнения лопастных насосов) [1]:
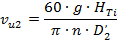
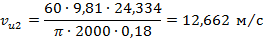
1.57. Угловой шаг лопатки [1]:
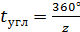
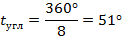
1.58. Угол охвата лопатки (угол между точками струек на входной и выходной кромках лопатки) [5]:
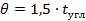
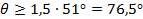
Конструктивно принимаем 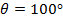
1.59. Ширина канала колеса в меридиональном сечении на диаметре D1 [1]:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 16 |
| КР ЛГМ и ГДП |
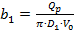 ,
,
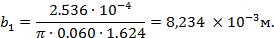
Из конструктивных соображений 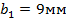 .
.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 17 |
| КР ЛГМ и ГДП |
ПОСТРОЕНИЕ МЕРИДИОНАЛЬНОГО СЕЧЕНИЯ РАБОЧЕГО КОЛЕСА И ГРАФИКА ПЛОЩАДЕЙ
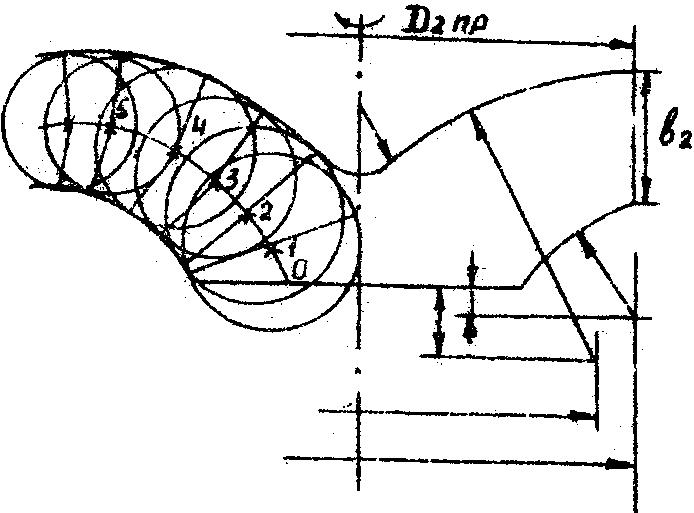
Вычерчиваем меридиональное сечение так, чтобы боковые очертания состояли из отрезков прямых и дуг круга. Строим нормальные сечения меридионального потока, изображаемые на чертеже нормальной линией (рис.1,а).
| 
|
| а | б |
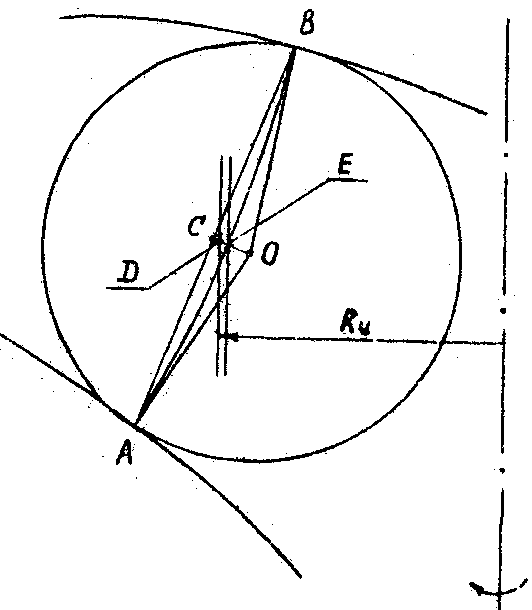
Рис.1. Построение меридионального сечения
Для этого вписываем окружности (рис.1,а) и из их центров в точки касания проводим радиусы. За нормальную линию может быть приближенно принята дуга АЕВ (рис.1,б), касающаяся радиусов ОА и ОВ в точках А и В. График F(l) строится так: от входа к выходу, вдоль линии центров l вписанных окружностей через шаг, равный, например, 1 см (точки намечаются измерителем на этой линии и на оси абсцисс графика F(l)), подсчитывается длина дуги нормальной линии lп. Поверхность вращения, образованная этой нормальной линией, дает площадь сечения F канала колеса. Приближенно длина дуги равна
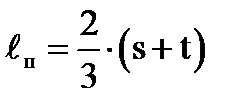 ,(61)
,(61)
где 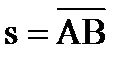 ;
; 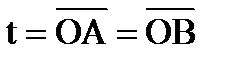 .
.
Площадь сечения канала равна
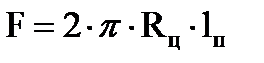 ,(62)
,(62)
где 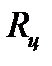 – радиус центра тяжести дуги lп.
– радиус центра тяжести дуги lп.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 18 |
| КР ЛГМ и ГДП |
Центр тяжести дуги расположен на прямой ОС, перпендикулярной хорде АВ, в точке D, отстоящей от точки С на расстоянии CD=ОС/3. На участке поворота потока площадь F следует увеличить на 20-40% по сравнению с площадью сечения горловины колеса 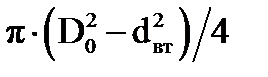 для компенсации стеснения проходной площади лопатками, которые начинаются в этой области. Кроме того, на повороте возникает неравномерное распределение скоростей по сечению из-за кривизны канала. Возрастание площади сечения канала на участке поворота приводит к увеличению радиуса кривизны внешнего очертания канала и, следовательно, к более равномерному распределению скоростей по сечению. Это уменьшает гидравлические потери.
для компенсации стеснения проходной площади лопатками, которые начинаются в этой области. Кроме того, на повороте возникает неравномерное распределение скоростей по сечению из-за кривизны канала. Возрастание площади сечения канала на участке поворота приводит к увеличению радиуса кривизны внешнего очертания канала и, следовательно, к более равномерному распределению скоростей по сечению. Это уменьшает гидравлические потери.
Результаты расчетов сведем в табл.1, в которой значения s, t, Rц , lп и l(длина вдоль линии центров от входа) снимаются с чертежа (см. прил.1).
Таблица 1. Результаты расчета для построения меридионального сечения.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, мм | 0 | 14 | 37,8 | 46,5 | 52 | 60 | 92 | 120,87 | 143,1 |
| lп, мм | 19.5 | 19.5 | 16,67 | 14,03 | 12,84 | 12 | 10,847 | 9,8 | 9 |
| Rц, мм | 27 | 27 | 30,07 | 33,7 | 36 | 38,5 | 54,5 | 68,9 | 80 |
| s, мм | 39 | 39 | 27 | 20 | 18,3 | 16.5 | 14,3 | 12,3 | 5 |
| t, мм | 9 | 9 | 8,6 | 7,25 | 6,56 | 6 | 5,42 | 4,9 | 4,5 |
| F, мм2 | 4350 | 4350 | 3664 | 3154 | 3082 | 3991 | 4061 | 5433 | 2985 |
По результатам расчетов строим график зависимости F(l) (см. прил.2).
1.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 19 |
| КР ЛГМ и ГДП |
РАЗБИЕНИЕ ПОВЕРХНОСТЯМИ ТОКА
В основе приближенного построения поверхностей тока лежат предположения:
· поверхности тока являются поверхностями вращения, независимо от воздействия лопаток на поток;
· в качестве нормальных линий к искомым поверхностям тока условно принимаем нормальные линии, полученные ранее;
· принимаем равномерное распределение меридиональной слагающей абсолютной скорости 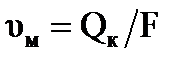 вдоль нормальной линии.
вдоль нормальной линии.
Все это достаточно справедливо для радиальных рабочих колес. Отклонение от строгого решения будет тем больше, чем больше ns.
Для линии 0-0 на входе (горловина колеса) имеем:
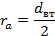
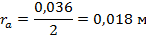
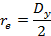
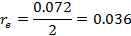
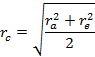
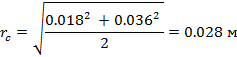
Далее двигаясь от входа к выходу, разбиваем нормальные линии на участки, образующие равные площади вращения.
Площади определяются:
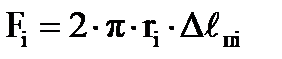 ,
,
где ri, 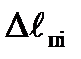 - см. рис.2.
- см. рис.2.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 20 |
| КР ЛГМ и ГДП |
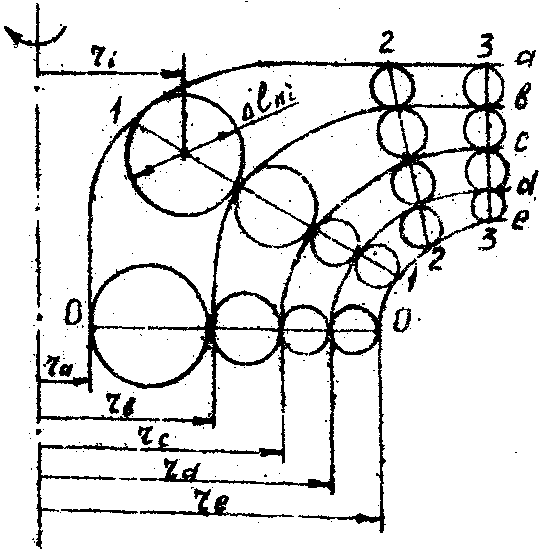
Рис. 2. Построение промежуточных поверхностей тока
Результаты расчета сведем в табл.2.
Таблица 2.
| 0 | 1 | 2 | 3 | |||||
| Δlпi, мм | 10 | 8 | 9 | 7,7 | 6 | 6 | 4,5 | 4,5 |
| ri, мм | 23 | 32 | 26 | 33 | 38,5 | 38,5 | 80 | 80 |
| Fi, мм2 | 1445 | 1608 | 1470 | 1597 | 1451 | 1451 | 2262 | 2262 |
Разбиение поверхностями тока представлено в приложении 3.
2. РАЗБИЕНИЕ НА ПАРАЛЛЕЛИ
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 21 |
| КР ЛГМ и ГДП |
При проведении меридианов выбирают Δφ =50-100. Радиус R удобно выбирать так, чтобы ΔS выражалось круглым числом миллиметров. Независимо от размеров проектируемого колеса радиус R следует выбирать в диапазоне от 150 до 200 мм. Выражая Δφ в градуса, получим:
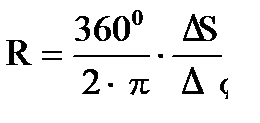
где ΔS=34мм; Δφ=100; ΔL=20мм.
|
|
|
|
|
|
|
|
|
|
| мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 22 |
| КР ЛГМ и ГДП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 23 |
| КР ЛГМ и ГДП |
Результаты расчетов сведем в таблицу 3.
Таблица 3.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Δ li, мм | 7,813 | 7,052 | 6,365 | 5,746 | 5,186 | 4,681 | 4,225 | 3,813 | 3,442 | 3,1 |
| rср , мм | 76,104 | 68,692 | 62,002 | 55,963 | 50,512 | 45,593 | 41,152 | 37,144 | 33,526 | 30,26 |
Графическое изображение разбиения на параллели приведено в приложении 4.
3.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 24 |
| КР ЛГМ и ГДП |
ПОСТРОЕНИЕ ПЛАНОВ СКОРОСТЕЙ
5.1. Построение планов скоростей на входе в рабочее колесо.
Строим три плана скоростей, т.к. на входе имеем три поверхности тока c, a и е, и определяем относительную скорость W1 и угол β1. Предварительная закрутка потока отсутствует. Построение ведем в соответствии с методикой, описанной в [5] (см.прил.5). Результаты вычислений сведем в таблицу 4.
Таблица 4.
| β 1л | Δβ | β1 | U 1 , м/с | υм1, м/с | W 1 , м/с | |
| Для средней струйки (c) | 260 | 70 | 190 | 11,692 | 4,062 | 12,37 |
| Для ведущего диска (a) | 280 | 100 | 180 | 3,881 | 12,28 | |
| Для ведомого диска ( е ) | 220 | 30 | 190 | 4,062 | 12,37 |
Здесь:
· U1 – окружная скорость на входе в рабочее колесо;
· υм1 – меридиональная составляющая абсолютной скорости на входе в рабочее колесо;
· W1 – относительная скорость на входе в рабочее колесо.
5.2. Построение плана скоростей на выходе рабочего колеса.
Построим план скоростей на выходе рабочего колеса в соответствии с методикой, описанной в [5] (см.прил.6) по известным величинам: β2л, U2, υм2, υм2∞, υu2, υu2∞. Из плана скоростей найдем значения неизвестных углов и скоростей. Результаты сведем в таблицу 5.
Таблица 5.
| β 2 | U2 , м/с | υм2, м/с | υ u2 , м/с | α 2 | W 2 , м/с | υ 2 , м/с | |
| Для конечного числа лопаток | 130 | 23,702 | 20,88 | 14,648 | 40 | 9,309 | 14,8 |
| Для бесконечного числа лопаток | 350 | 2,088 | 20,636 | 90 | 3,724 | 20,74 |
Здесь:
· U2 – окружная скорость на выходе из рабочего колеса;
· υ2 – абсолютная скорость жидкости на выходе из рабочего колеса;
·
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 25 |
| КР ЛГМ и ГДП |
υм2 – меридиональная составляющая абсолютной скорости на выходе из рабочего колеса;
· υu2 – окружная составляющая абсолютной скорости на выходе из рабочего колеса;
· W1 – относительная скорость на входе в рабочее колесо.
4.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 26 |
| КР ЛГМ и ГДП |
ПОСТРОЕНИЕ КОНФОРМНОЙ ДИАГРАММЫ
Поверхность тока представляет собой поверхность вращения, которая в общем случае не развертывается на плоскость. Это затрудняет профилирование лопатки, т.е. построение линии пересечения поверхности лопатки с поверхностями тока. Поэтому широкое распространение получило конформное отображение поверхности тока на поверхность вращения, которую можно развернуть на плоскость. Такой поверхностью будет коническая поверхность и в пределе – плоскость перпендикулярная оси, а так же круглый цилиндр. Под конформным отображением одной поверхности на другую понимается такое соответствие точек поверхностей, при котором величина угла между любыми пересекающимися линиями сохраняется.
У лопатки имеются две поверхности, называемые лицевой и тыльной. Вследствие конечной толщины лопатки форма этих поверхностей различна. Задача профилирования – найти обе поверхности лопатки. В качестве расчетной следует принять среднюю поверхность между лицевой и тыльной сторонами. После расчета этой поверхности производим необходимые построения на чертеже, позволяющие изготовить обе стороны лопатки.
Струйка должна иметь монотонно изменяющийся угол от β1л до β2л.
Участок лопатки вблизи выхода должен иметь постоянный угол β2л на длине примерно 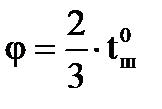 , где
, где 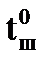 - угловой шаг лопатки.
- угловой шаг лопатки.
Угол охвата лопатки Θ должен быть больше шагового угла лопаток. Описание построения конформной диаграммы приведено в [6].
Для построения принимаем
ΔS=30мм;
Δφ=100;
ΔL=20мм.
Конформная диаграмма приведена в приложении 6.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 27 |
| КР ЛГМ и ГДП |
ЗАКЛЮЧЕНИЕ
В результате выполнения курсовой работы выбран тип насоса и рабочего колеса, проведен расчет основных конструктивных параметров насоса, построено меридиональное сечение рабочего колеса, построены планы скоростей на входе и выходе рабочего колеса. Также построена конформная диаграмма по результатам разбиения меридионального сечения на струйки тока и параллели.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 28 |
| КР ЛГМ и ГДП |
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Михайлов А.К., Малюшенко В.В. Конструкция и расчет центробежных насосов высокого давления. М.: Машиностроение, 1971, 304с.
2. Башта Т. М., Руднев С. С., Некрасов Б. Б. и др. Гидравлика, гидромашины и гидроприводы. М.: Машиностроение, 1982, 423с.
3. Ломакин Н.А. Центробежные и осевые насосы. М.: Машиностроение, 1966, 364с.
4. Байбаков О.В. и др. Лабораторный курс гидравлики, насосов и гидропередач. М.: Машиностроение, 1974, 416с.
5. Руднев С.С, Матвеев И.В. Методическое пособие по курсовому проектированию лопастных насосов. М.: изд. МВТУ им. Н.Э. Баумана, 1974, 71с.
6. Воронов С.А., Микипорис Ю.А. Расчет и проектирование рабочего колеса лопастного насоса. Владимир, изд. ВПИ, 1989, 35с.









 мм
мм
 мм
мм мм
мм


 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм
 мм
мм