Этап 2. Определение вектора приоритетов
В качестве вектора приоритетов для каждого уровня иерархии принят нормализованный главный собственный вектор матрицы попарных сравнений. Для расчета этих векторов используется приближенный метод 4 из [1] оценки через средние геометрические.
Собственный вектор обеспечивает упорядочение приоритетов. Чем больше i-я компонента СВ, тем больше влияние i-го элемента в комплексе всех элементов анализируемого уровня иерархии на выделенный элемент С вышестоящего уровня.
Таким образом, все векторы приоритетов для второго и третьего уровней иерархии получены.
Этап 3. Определение максимальных собственных значений и степени согласованности матриц парных сравнений
Прежде чем перейти к синтезу оптимальной альтернативы с учетом всех элементов второго и третьего уровней иерархии, нужно убедиться в достаточном уровне согласованности всех матриц суждений Ас.1, Ас.2, Ас.2, Ас.4. Для этого нужно вычислить максимальные собственные значения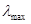 
этих матриц. В теории МАИ приводится следующий алгоритм [1] расчета 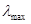. Сначала суммируется каждый столбец суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца – на вторую компоненту и т.д. Затем полученные числа суммируются:
, 
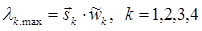(8)
где k – номер матрицы парных сравнений (суждений);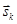 
– вектор-строка столбцовых сумм матрицы суждений с номером k; 
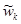– нормализованный собственный главный вектор матрицы суждений Ас.k, принадлежащий наибольшему собственному значению 
.
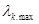Этап 4. Определение индексов согласованности и отношений согласованности для матриц суждений
В общем случае под согласованностью понимается то, что при наличии основного (базового) массива необработанных данных все другие данные логически могут быть получены из них. Или другими словами, отношения элементов всей матрицы А не должны быть противоречивыми.
Из теории МАИ известно, что идеальная согласованность положительной обратносимметричной матрицы эквивалентна требованию
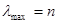
Заметим, что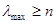 
всегда верно, поэтому
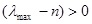
Тогда степень согласованности матрицы суждений можно оценить мерой, называемой индексом согласованности (ИС)
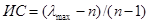. (9)
Знаменатель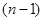 
– это число всех возможных парных сравнений данного элемента 
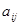в фиксированной строке i для квадратной матрицы n-го порядка.
Следовательно, ИС имеет смысл отклонения от абсолютной согласованности, приходящегося на одно парное сравнение.
Вводится критерий, называемый отношением согласованности (ОС):
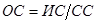, (10)
где СС – индекс случайной согласованности (СС).
СС определяется путем задания оценок по шкале отношений для случайно выбранных суждений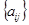 
при парных сравнениях и соответствующих им обратных величин для матрицы А. Значения СС в теории МАИ заранее вычислены и представлены в таблице 7.
Таблица 7
Случайная согласованность для случайных матриц
| Порядок матрицы n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Случайная согласованность СС | 0 | 0 | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Приемлемая величина ОС – порядка 10% или менее. Если ОС выходит из этих пределов, то ЛПР должно провести более глубокие исследования задачи и проверить свои суждения, т.е. назначение величин 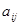в матрице парных сравнений.
Этап 5. Синтез приоритетов уровней
В математической теории иерархий разработан метод оценки воздействия уровня на соседний вышестоящий уровень путем композиции соответствующего вклада (приоритетов) элементов данного уровня по отношении к каждому элементу соседнего верхнего уровня. Композиция распространяется снизу-вверх. В принципе, можно рассматривать также распространение композиции сверху-вниз.
Математически «композиция» отображается оператором умножения. Как известно [3], в математической логике операция умножения отображает совместное действие сомножителей.
Приоритеты синтезируются, начиная со второго уровня вниз. Локальные приоритеты (приоритеты альтернатив А1, А2, А3, А4,А5 по каждому критерию) перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии критериями на которые воздействует этот элемент. Процедура продолжается до самого нижнего уровня. В формализованном виде процедура синтеза приоритетов имеет следующий вид.
Общий вектор приоритетов взаимного влияния уровня 3 альтернатив (А1, А2, А3, А4,А5) и уровня 2 критериев (К1, К2, К3,К4,К5) на общую цель (уровень 1) равен:
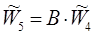, (11)
где В – матрица компонент нормированных векторов приоритетов альтернатив первого снизу уровня (см. таблицы 2, 3 и 4);
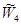– нормированный вектор приоритета критериев второго уровня (таблица 5).
Для нашего примера:
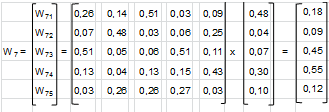
Этап 6. Выбор оптимальной альтернативы
Алгоритм оптимального выбора прост:
Таким образом, алгоритм оптимального многокритериального выбора приводит к выбору языка программирования №4 (С++), так как ему соответствует наибольшее значение компонента вектора общего приоритета 0,55.