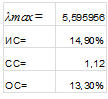Задание 2. Построение модели многокритериального выбора альтернатив с использованием метода анализа иерархий
Выбор языка программирования или интегрированной среды разработки приложений (для разработки некоторого конкретного программного продукта). Предпочтительность альтернатив оценивать с позиций качества разрабатываемых приложений, сроков разработки, требований к квалификации разработчиков либо уровня их квалификации в отношении той или иной среды и т.п.
Целью данной работы: Выбор языка программирования или интегрированной среды разработки приложений (для разработки некоторого конкретного программного продукта)с использованием МАИ.
В работе решаются следующие задачи:
- поиск и выбор объектов для оценки,
- формулирование задачи выбора,
- расстановка оценок объектов по критериям и уровням иерархии,
- итоговое свертывание по нормированным оценкам и принятие решения о выборе проекта.
Пример:
Нужно произвести выбор языка программирования.
Оценивается пять платформ:
1. Jawa . Имеет мало внешних зависимостей, предназначен для работы на любой физической машине,
2. PHP . Язык с открытым исходным кодом (скриптовый), применяется для WEB разработок, код на нем без проблем внедряется в HTML код.
3. Perl . Высокоуровневый интерпретируемый динамический язык программирования. Основной особенностью языка считаются его богатые возможности для работы с текстом, в том числе работа с регулярными выражениями , встроенными в синтаксис.
4. С++. Компилируемый, статический типизированный язык программирования общего назначения, один из самых распространенных языков, отличительная особенность это быстрый процессинг и компиляция.
5. Delphi . Императивный, структурированный объектно ориентированный язык программирования со строгой статической типизацией переменных.
Отбор девушек происходит по пяти критериям:
1. Область применения.
2. Интерфейс
3. Функциональность.
4. Прибыльность.
5. Быстродействие.
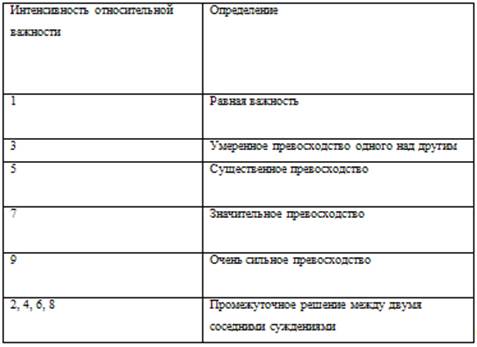
Для оценки используется следующая шкала относительной важности:
Таблица 1
Шкала относительной важности
Этап 1. Выполнение попарных экспертных сравнений элементов каждого уровня иерархий
Рассмотрим элементы С1, С2, …, Сn некоторого зафиксированного уровня иерархи. Мы хотим определить веса ѡ1, ѡ2, …,ѡn влияния этих элементов на некоторый элемент вышестоящего уровня. Основным инструментом оценки влияния является матрица чисел по шкале отношений 1, …, 9 (табл. 1), представляющих суждения о парных сравнениях. Для представления приоритетов в МАИ выбран собственный вектор, принадлежащий наибольшему собственному значению указанной матрицы А. Обозначим через 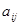 число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня
число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня
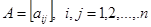 . (5)
. (5)
Матрица А с содержательной точки зрения, будет согласованной по оценкам при введении условия
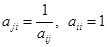 . (6)
. (6)
С математической точки зрения это условие наделяет матрицу А свойством обратно-симметричной матрицы. На главной диагонали матрицы А стоят 1.
Если оценки попарных сравнений известны точно, т.е. оценки основаны на экспериментальных измерениях, то
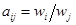 , (7)
, (7)
т.е. веса влияния элементов известны.
Например, если взвешиваются два предмета: С1=305,2 и С2=244,2, тогда отношение 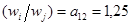 означает, что предмет С1 в 1,25 раз тяжелее предмета С2.
означает, что предмет С1 в 1,25 раз тяжелее предмета С2.
Для случая экспериментального измерения весов ѡ1, ѡ2, …,ѡi,…, ѡn сравниваемых элементов на уровне иерархии согласованность считается полной, естественно, с точностью до погрешности измерительных приборов или расчетных методик. При экспертной оценке отношений (7) согласованность суждений и соответственно матрицы А будет не полной. Значит нужно разработать некоторую числовую меру отклонения согласованности матрицы А от идеальной (см. ниже формулу отношения согласованности (9).
Теперь рассмотрим подробнее содержательный смысл требования согласованности в МАИ.
В МАИ под согласованностью суждений подразумевается не просто традиционное требование транзитивности предпочтений [3]: если например, для индивидуума яблоки предпочтительнее апельсинов, а апельсины предпочтительнее бананов, то яблоки должны быть предпочтительнее бананов.
Схематически это можно записать так:
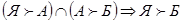 .
.
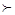 – знак предпочтения элемента в отношении двух элементов;
– знак предпочтения элемента в отношении двух элементов;
∩ – знак пересечения множеств (совместности).
В МАИ транзитивность наделяется количественными отношениями. Например, если яблоки в 2 раза предпочтительнее апельсин (по цене), а апельсины предпочтительнее бананов в 3 раза, то яблоки должны быть в 6 раз предпочтительнее бананов. Именно это автор МАИ Саати называет числовой (кардинальной) согласованностью предпочтений. Несогласованность означает отсутствие пропорциональности, которое может нарушить транзитивность.
МАИ не только показывает наличие несогласованности отдельных сравнений, но и дает численную оценку того, как сильно нарушена согласованность для всей рассматриваемой задачи.
Замечание. В простейшей версии МАИ считается, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы между собой, но все они влияют на каждый элемент другого (вышестоящего) уровня. Таким образом, общая задача многокритериального выбора сводится к задаче оценки влияния уровней иерархи (снизу-вверх либо сверху-вниз). иерархия экспертный приоритет альтернатива
Теперь обратимся к расчетам для нашего примера.
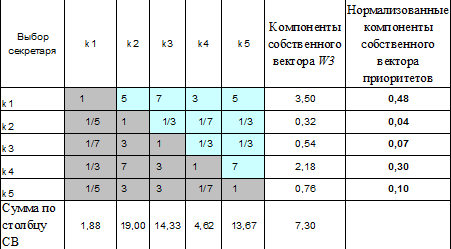
Зафиксируем нижний (третий) уровень иерархи Рис. 2, содержащий элементы А1, А2, А3, А4, А5 претендентов на должность. Зафиксируем также один элемент К1 –знание делопроизводства на уровне 2 иерархии.
Матрица АС.1 парных сравнений альтернатив по первому критерию
Таблица 2
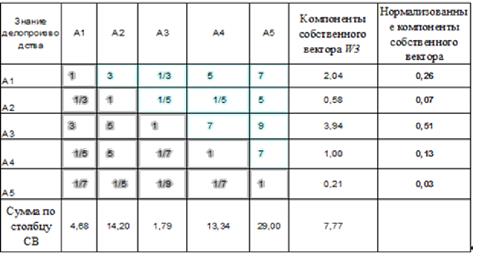

| ИС= | 17,82% |
| СС= | 1,12 |
| ОС= | 15,91% |
Аналогично поступим с остальными критериями
Таблица 3
Матрица АС.2 парных сравнений альтернатив по первому критерию
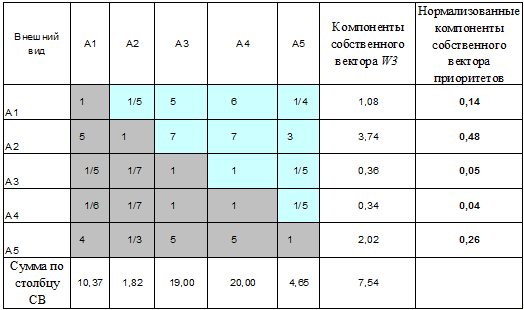
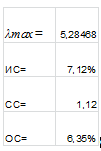
Таблица 4
Матрица АС.2 парных сравнений альтернатив по первому критерию
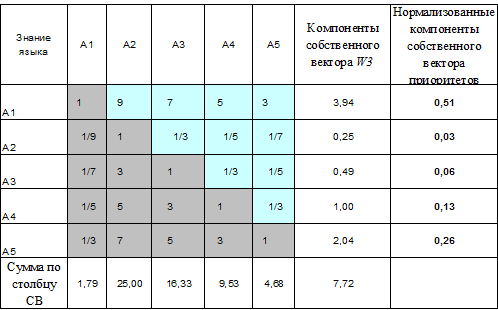
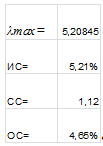
Таблица 5
Матрица АС.2 парных сравнений альтернатив по первому критерию
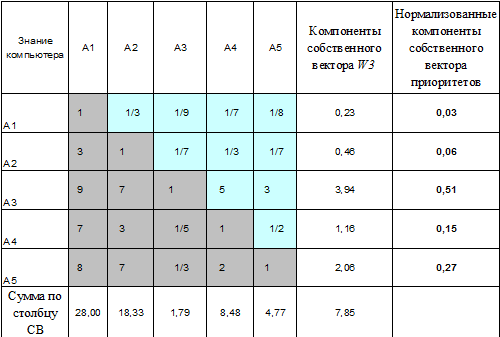
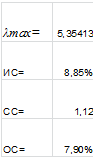
Таблица 6
Матрица АС.2 парных сравнений альтернатив по первому критерию
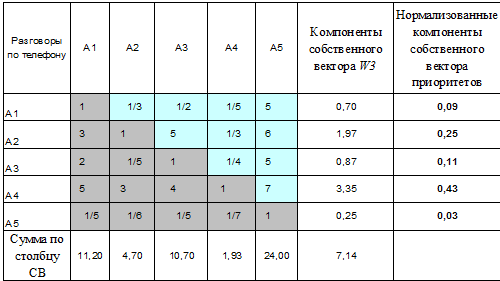
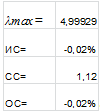
Таблица 7
Матрица АС.4 парных сравнений критериев