2. Кэт расшифровывает сообщение, также используя ключ KА.
Методы и средства защиты информации
Лекция 7
Симметричные криптосистемы (продолжение)
2. Хеширование паролей
Для того, чтобы не заставлять человека запоминать ключ – длинную последовательность цифр, были разработаны методы преобразования строки символов любой длины (так называемого пароля) в блок байт заранее заданного размера (ключ). На алгоритмы, используемые в этих методах, накладываются требования, сравнимые с требованиями на сами криптоалгоритмы.
От методов, повышающих криптостойкость системы в целом, перейдем к блоку хеширования паролей – методу, позволяющему пользователям запоминать не 128 байт, то есть 256 шестнадцатиричных цифр ключа, а некоторое осмысленное выражение, слово или последовательность символов, называющуюся паролем. Действительно, при разработке любого криптоалгоритма следует учитывать, что в половине случаев конечным пользователем системы является человек, а не автоматическая система. Это ставит вопрос о том, удобно, и вообще реально ли человеку запомнить 128-битный ключ (32 шестнадцатиричные цифры). На самом деле предел запоминаемости лежит на границе 8-12 подобных символов, а, следовательно, если мы будем заставлять пользователя оперировать именно ключом, тем самым мы практически вынудим его к записи ключа на каком-либо листке бумаги или электронном носителе, например, в текстовом файле. Это, естественно, резко снижает защищенность системы.
Для решения этой проблемы были разработаны методы, преобразующие произносимую, осмысленную строку произвольной длины – пароль – в указанный ключ заранее заданной длины. В подавляющем большинстве случаев для этой операции используются так называемые хеш-функции (от англ. hashing – мелкая нарезка и перемешивание). Напомним:
Хэш (Hash) - блок данных фиксированного размера, полученный в результате хэширования массива данных.
Хэширование (Hashing) - в криптографии - преобразование массива данных произвольного размера в блок данных фиксированного размера, служащий (в некоторых случаях) заменителем исходного массива. Хеширование выполняется с помощью хэш-функций.
Хэш-функция (Hash-function) – функция (математическое или логическое преобразование), осуществляющая хэширование массива данных посредством отображения значений из (очень) большого множества значений в (существенно) меньшее множество значений. Под хэш-функцией понимается процедура получения контрольной характеристики двоичной последовательности, основанная на контрольном суммировании и криптографических преобразованиях.
Хеш-функция отображает сообщения произвольной длины в короткие блоки фиксированной длины. Хеш-функция обладает следующими свойствами:
1. хеш-функция имеет бесконечную область определения,
2. хеш-функция имеет конечную область значений,
3. она необратима, т.е. это требование односторонности хэш-функции: легко создать хэш-код по данному сообщению, но невозможно восстановить сообщение по данному хэш-коду;
4. изменение входного потока информации на один бит меняет около половины всех бит выходного потока, то есть результата хеш-функции.
Однонаправленная функция Н(М) применяется к сообщению произвольной длины М и возвращает значение фиксированной длины h:
h = Н(М),
где h имеет длину т.
Многие функции позволяют вычислять значение фиксированной длины по входным данным произвольной длины, но у однонаправленных хэш-функций есть дополнительные свойства, делающие их однонаправленными.
Зная М, легко вычислить h.
Зная Н, трудно определить М, для которого H( M)= h.
Зная М, трудно определить другое сообщение, М’, для которого Н(М)=Н(М’)'
Эти свойства позволяют подавать на вход хеш-функции пароли, то есть текстовые строки произвольной длины на любом национальном языке и, ограничив область значений функции диапазоном 0..2N-1, где N – длина ключа в битах, получать на выходе достаточно равномерно распределенные по области значения блоки информации – ключи.
Невозможно найти другое сообщение, чье значение хэш-функции совпадало бы со значением хэш-функции данного сообщения. Это предотвращает подделку аутентификатора при использовании зашифрованного хэш-кода. В данном случае противник может читать сообщение и, следовательно, создать его хэш-код. Но так как противник не владеет секретным ключом, он не имеет возможности изменить сообщение так, чтобы получатель этого не обнаружил. Если данное свойство не выполняется, атакующий имеет возможность выполнить следующую последовательность действий: перехватить сообщение и его зашифрованный хэш-код, вычислить хэш-код сообщения, создать альтернативное сообщение с тем же самым хэш-кодом, заменить исходное сообщение на поддельное. Поскольку хэш-коды этих сообщений совпадают, получатель не обнаружит подмены.
Еще одно свойство защищает против класса атак, известных как атака "день рождения". Так называемый "парадокс дня рождения" (файл INTUIT_ru Курс Криптографические __ Лекция №8 Хэш-функции и аутентификация сообщений_ Часть 1_стр2.htm) состоит в следующем. Предположим, количество выходных значений хэш-функции Н равно n. Каким должно быть число k, чтобы для конкретного значения X и значений Y1, …, Yk вероятность того, что хотя бы для одного Yi выполнялось равенство H(X) = H(Y) была бы больше 0,5.
Путем определенных вычислений выясняется, что для m-битового хэш-кода достаточно выбрать 2m-1 сообщений, чтобы вероятность совпадения хэш-кодов была больше 0,5.
Теперь рассмотрим следующую задачу: обозначим P (n, k) вероятность того, что в множестве из k элементов, каждый из которых может принимать n значений, есть хотя бы два с одинаковыми значениями. Чему должно быть равно k, чтобы P (n, k) была бы больше 0,5?
Если хэш-код имеет длину m бит, т.е. принимает 2m значений, то
k = √2m = 2m/2
Подобный результат называется "парадоксом дня рождения", потому что в соответствии с приведенными выше рассуждениями для того, чтобы вероятность совпадения дней рождения у двух человек была больше 0,5, в группе должно быть всего 23 человека. Этот результат кажется удивительным, возможно, потому, что для каждого отдельного человека в группе вероятность того, что с его днем рождения совпадет день рождения кого-то другого в группе, достаточно мала.
Тем не менее, возможны различного рода атаки, основанные на "парадоксе дня рождения". Возможна следующая стратегия:
1. Противник создает 2m/2 вариантов сообщения, каждое из которых имеет некоторый определенный смысл. Противник подготавливает такое же количество сообщений, каждое из которых является поддельным и предназначено для замены настоящего сообщения.
2. Два набора сообщений сравниваются в поисках пары сообщений, имеющих одинаковый хэш-код. Вероятность успеха в соответствии с "парадоксом дня рождения" больше, чем 0,5. Если соответствующая пара не найдена, то создаются дополнительные исходные и поддельные сообщения до тех пор, пока не будет найдена пара.
3. Атакующий предлагает отправителю исходный вариант сообщения для подписи. Эта подпись может быть затем присоединена к поддельному варианту для передачи получателю. Так как оба варианта имеют один и тот же хэш-код, будет создана одинаковая подпись. Противник будет уверен в успехе, даже не зная ключа шифрования.
Нетрудно заметить, что требования, предъявляемые к хеш-функции, выполняют блочные шифры. Это указывает на один из возможных путей реализации стойких хеш-функций – проведение блочных криптопреобразований над материалом строки-пароля. Этот метод и используется в различных вариациях практически во всех современных криптосистемах. Материал строки-пароля многократно последовательно используется в качестве ключа для шифрования некоторого заранее известного блока данных – на выходе получается зашифрованный блок информации, однозначно зависящий только от пароля и при этом имеющий достаточно хорошие статистические характеристики. Такой блок или несколько таких блоков и используются в качестве ключа для дальнейших криптопреобразований.
Характер применения блочного шифра для хеширования определяется отношением размера блока используемого криптоалгоритма и разрядности требуемого хеш-результата.
Если указанные выше величины совпадают, то используется схема одноцепочечного блочного шифрования. Первоначальное значение хеш-результата H0 устанавливается равным 0, вся строка-пароль разбивается на блоки байт, равные по длине ключу используемого для хеширования блочного шифра, затем производятся преобразования по реккурентной формуле:
Hj=Hj-1 XOR EnCrypt(Hj-1, PSWj),
где EnCrypt(X, Key) – используемый блочный шифр (рис.1);
PSWj – материал строки пароля.
Последнее значение Hk используется в качестве искомого результата.
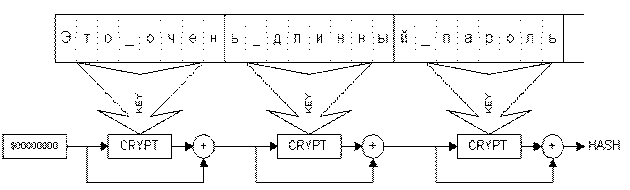
Рис. 1.
В том случае, когда длина ключа ровно в два раза превосходит длину блока, а подобная зависимость довольно часто встречается в блочных шифрах, используется схема, напоминающая сеть Фейштеля. Характерным недостатком и приведенной выше формулы, и хеш-функции, основанной на сети Фейштеля, является большая ресурсоемкость в отношении пароля. Для проведения только одного преобразования, например, блочным шифром с ключом длиной 128 бит используется 16 байт строки-пароля, а сама длина пароля редко превышает 32 символа. Следовательно, при вычислении хеш-функции над паролем будут произведено максимум 2 "полноценных" криптопреобразования.
Решение этой проблемы можно достичь двумя путями: 1) предварительно "размножить" строку-пароль, например, записав ее многократно последовательно до достижения длины, скажем, в 256 символов; 2) модифицировать схему использования криптоалгоритма так, чтобы материал строки-пароля "медленнее" тратился при вычислении ключа.
По второму пути пошли исследователи Девис и Майер, предложившие алгоритм также на основе блочного шифра, но использующий материал строки-пароля многократно и небольшими порциями. В нем просматриваются элементы обеих приведенных выше схем, но криптостойкость этого алгоритма подтверждена многочисленными реализациями в различных криптосистемах. Алгоритм получил название "Tandem DM" (рис.2): В качестве стартового вектора хэширования принимают, например, нулевой вектор.
G0=0; H0=0 ;
FOR J = 1 TO N DO
BEGIN
TMP=EnCrypt(H, [G, PSWj]); H'=H XOR TMP;
TMP=EnCrypt(G, [PSWj, TMP]); G'=G XOR TMP;
END;
Key=[Gk, Hk]
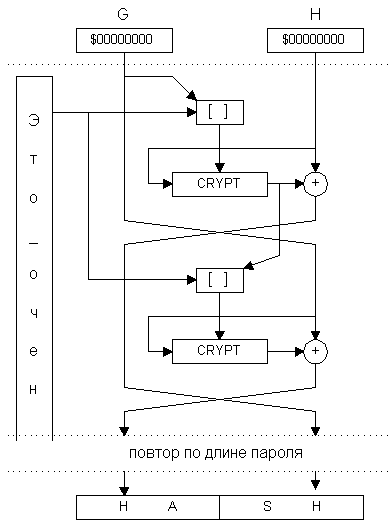
Рис. 2.
Квадратными скобками (X16=[A8, B8]) здесь обозначено простое объединение (склеивание) двух блоков информации равной величины в один – удвоенной разрядности. А в качестве процедуры EnCrypt(X, Key) опять может быть выбран любой стойкий блочный шифр. Как видно из формул, данный алгоритм ориентирован на то, что длина ключа двукратно превышает размер блока криптоалгоритма. А характерной особенностью схемы является тот факт, что строка пароля считывается блоками по половине длины ключа, и каждый блок используется в создании хеш-результата дважды. Таким образом, при длине пароля в 20 символов и необходимости создания 128 битного ключа внутренний цикл хеш-функции повторится 3 раза.
Итерационный процесс вычисления хэш-функции по ГОСТ 28147-89 предусматривает:
- генерацию четырех ключей (слов длиной 256 бит);
- шифрующее преобразование с помощью ключей текущего значения Н методом простой замены;
- перемешивание результатов;
- поразрядное суммирование по mod2 слов длиной 256 бит исходной последовательности;
- вычисление функции Н.
В результате получается хэш-функция длиной 256 бит. Значение хэш-функции можно хранить вместе с контролируемой информацией, т.к. не имея стартового вектора хэширования, злоумышленник не может получить новую правильную функцию хэширования после внесения изменений в исходную последовательность. А получить стартовый вектор по функции хэширования практически невозможно.
Для каждой двоичной последовательности используются две контрольные характеристики: стартовый вектор и хэш-функция. При контроле по стартовому вектору и контролируемой последовательности вычисляется значение хэш-функции и сравнивается с контрольным значением.
3.Транспортное кодирование
В некоторых системах передачи информации требуется, чтобы поток содержал только определенные символы ASCII кодировки. Однако выходной поток криптоалгоритма имеет очень высокую рандомизацию и в нем встречаются с равной вероятностью все 256 символов. Для преодоления этой проблемы используется транспортное кодирование.
Поскольку системы шифрования данных часто используются для кодирования текстовой информации: переписки, счетов, платежей электронной коммерции, и при этом криптосистема должна быть абсолютно прозрачной для пользователя, то над выходным потоком криптосистемы часто производится транспортное кодирование, то есть дополнительное кодирование (не шифрование!) информации исключительно для обеспечения совместимости с протоколами передачи данных и чтобы гарантировать безопасную его транспортировку через сеть.
Все дело в том, что на выходе криптосистемы байт может принимать все 256 возможных значений, независимо от того был ли входной поток текстовой информацией или нет. А при передаче почтовых сообщений многие системы ориентированы на то, что допустимые значения байтов текста лежат в более узком диапазоне: все цифры, знаки препинания, алфавит латиницы плюс, возможно, национального языка. Первые 32 символа набора ASCII служат для специальных целей. Для того, чтобы они и некоторые другие служебные символы никогда не появились в выходном потоке используется транспортное кодирование.
Наиболее простой метод состоит в записи каждого байта двумя шестнадцатиричными цифрами-символами (0123456789ABCDEF). Так байт 252 будет записан двумя символами 'FC'; байт с кодом 26, попадающий на специальный символ CTRL-Z, будет записан двумя допустимыми символами '1A'. Но эта схема очень избыточна: в одном байте передается только 4 бита информации.
На самом деле практически в любой системе коммуникации без проблем можно передавать около 68 символов (латинский алфавит строчный и прописной, цифры и знаки препинания). Из этого следует, что вполне реально создать систему с передачей 6 бит в одном байте (26<68), то есть кодировать 3 байта произвольного содержания 4-мя байтами из исключительно разрешенных (так называемых печатных) символов. Подобная система была разработана и стандартизирована на уровне протоколов сети Интернет – это система Base64 (стандарт RFC1251).
Процесс кодирования преобразует 4 входных символа в виде 24-битной группы, обрабатывая их слева направо. Эти группы затем рассматриваются как 4 соединенные 6-битные группы, каждая из которых транслируется в одиночную цифру алфавита base64. При кодировании base64 входной поток байтов должен быть упорядочен старшими битами вперед.
Каждая 6-битная группа используется как индекс для массива 64-х печатных символов. Символ, на который указывает значение индекса, помещается в выходную строку. Эти символы выбраны так, чтобы быть универсально представимыми и исключают символы, имеющие специальное значение (".", CR, LF – последние два являются частью последовательности разрыва строки).
Таблица 1
Алфавит Base64
Значение Код Значение Код Значение Код Значение Код
(6 бит) ASCII (6 бит) ASCII (6 бит) ASCII (6 бит) ASCII
0 A 17 (11) R 34 (22) I 51 (33) z
1 B 18 (12) S 35 (23) j 52 (34) 0
2 C 19 (13) T 36 (24) k 53 (35) 1
3 D 20 (14) U 37 (25) l 54 (36) 2
4 E 21 (15) V 38 (26) m 55 (37) 3
5 F 22 (16) W 39 (27) n 56 (38) 4
6 G 23 (17) X 40 (28) o 57 (39) 5
7 H 24 (18) Y 41 (29) p 58 (3A) 6
8 I 25 (19) Z 42 (2A) q 59 (3B) 7
9 J 26 (1A) a 43 (2B) r 60 (3C) 8
10 (A) K 27 (1B) b 44 (2C) s 61 (3D) 9
11 (B) L 28 (1C) c 45 (2D) t 62 (3E) +
12 (C) M 29 (1D) d 46 (2E) u 63 (3F) /
13 (D) N 30 (1E) e 47 (2F) v заполнитель =
14 (E) O 31 (1F) f 48 (30) w
15 (F) P 32 (20) g 49 (31) x
16 (10) Q 33 (21) h 50 (32) y
Выходной поток (закодированные байты) должен иметь длину строк не более 76 символов. Все признаки перевода строки и другие символы, отсутствующие в таблице 1, должны быть проигнорированы декодером base64. Среди данных в Base64 символы, не перечисленные в табл. 1, переводы строки и т.п. должны говорить об ошибке передачи данных, и, соответственно, программа-декодер должна оповестить пользователя о ней.
Если в хвосте потока кодируемых данных осталось меньше, чем 24 бита, справа добавляются нулевые биты до образования целого числа 6-битных групп. А до конца 24-битной группы может оставаться только от 0 до 3-х недостающих 6-битных групп, вместо каждой из которых ставится символ-заполнитель "=". Поскольку весь входной поток представляет собой целое число 8-битных групп (т.е., просто байтных значений), то возможны лишь следующие случаи:
1. Входной поток оканчивается ровно 24-битной группой (длина файла кратна 3). В таком случае выходной поток будет оканчиваться четырьмя символами Base64 без каких либо дополнительных символов.
2. "Хвост" входного потока имеет длину 8 бит. Тогда в конце выходного кода будут два символа Base64, с добавлением двух символов "=".
3. "Хвост" входного потока имеет длину 16 бит. Тогда в конце выходного будут стоять три символа Base64 и один символ "=".
Так как символ "=" является хвостовым заполнителем, его появление в теле письма может означать только то, что конец данных достигнут. Но опираться на поиск символа "=" для обнаружения конца файла неверно, так как, если число переданных битов кратно 24, то в выходном файле не появится ни одного символа "=". Любые символы, не входящие в алфавит base64-должны игнорироваться.
Следует позаботиться о том, чтобы использовались корректные октеты в качестве разделителей строк при работе с base64. В частности, разрывы строк должны быть преобразованы в последовательности CRLF до выполнения кодирования base64.
3.Общая схема симметричной криптосистемы
Схема объединения всех рассмотренных выше методов.
Общая схема симметричной криптосистемы с учетом всех рассмотренных пунктов изображена на рисунке 3.
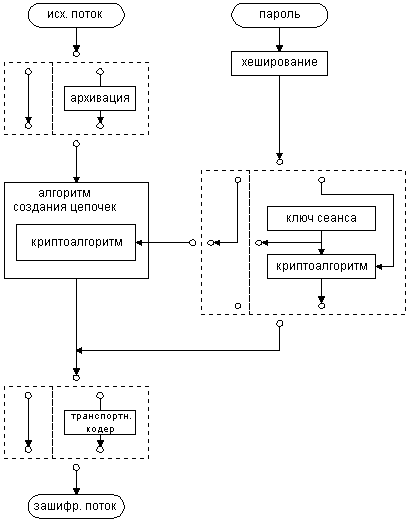
Рис.3. Симметричная криптосистема
Подпись документов при помощи симметричных криптосистем
Первые варианты цифровой подписи были реализованы при помощи симметричных криптосистем, в которой абоненты, участвующие в обмене сообщениями, используют один и тоже секретный ключ для простановки и проверки подписи под документом. В качестве алгоритма криптографического преобразования может использоваться любая из симметричных криптосистем, обладающая специальными режимами функционирования (например, DES, ГОСТ 28147-89 и т.п.).
Процедура подписи документов при помощи симметричной криптосистемы может выглядеть следующим образом:
1. Алекс и Юстас обладают одинаковым секретным ключом K.
2. Алекс зашифровывает цифровое сообщение, используя ключ K, и посылает зашифрованное сообщение Юстасу. При этом, как уже отмечалось, используется криптосистема, обладающая специальными механизмами функционирования, например ГОСТ 28147-89 в режиме выработки имитовставки.
3. Юстас расшифровывает сообщение при помощи ключа K.
Так как только Алекс и Юстас обладают секретным ключом, то тем самым обеспечивается гарантия, что сообщение подписано именно Алексом, а не стариком Мюллером. Однако, данная схема применима только в тех сетях, в которых можно дать стопроцентную гарантирую надежности каждого из абонентов, т.к. в обратном случае существует потенциальная возможность мошенничества со стороны одного из абонентов, владеющих секретным ключом.
Для устранения указанного недостатка была предложена схема с доверенным арбитром. В данной схеме помимо Алекса и Юстаса существует арбитр - радистка Кэт. Она может обмениваться сообщениями и с Алексом, и с Юстасом, и владеет секретными ключами обоих - KА и KЮ. Процедура подписания документов в данной схеме выглядит следующим образом:
1. Алекс зашифровывает сообщение, используя ключ KА, и посылает его Кэт.
2. Кэт расшифровывает сообщение, также используя ключ KА.
3. Расшифрованное сообщение Кэт зашифровывает на ключе Юстаса KЮ.
4. Данное сообщение Кэт посылает Юстасу.
5. Юстас расшифровывает сообщение, полученное от Кэт, используя ключ KЮ.
Насколько эффективна данная схема? Рассмотрим ее с учетом вышеуказанных требований, предъявляемых к цифровой подписи.
Во-первых, Кэт и Юстас знают, что сообщение пришло именно от Алекса. Уверенность Кэт основана на том, что секретный ключ KА имеют только Алекс и Кэт. Подтверждение Кэт служит доказательством Юстасу. Во-вторых, только Алекс знает ключ KА (и Кэт, как доверенный арбитр). Кэт может получить зашифрованное сообщение на ключе KА только от Алекса. Если Мюллер пытается послать сообщение от имени Алекса, то Кэт сразу обнаружит это на 2-м шаге. В-третьих, если Юстас пытается использовать цифровую подпись, полученную от Кэт, и присоединить ее к другому сообщению, выдавая его за сообщение от Алекса, это выявляется. Арбитр может потребовать от Юстаса данное сообщение и затем сравнивает его с сообщением, зашифрованном на ключе KА. Сразу выявляется факт несоответствия между двумя сообщениями. Если бы Юстас попытался модифицировать присланное сообщение, то Кэт аналогичным способом выявила бы подделку. В-четвертых, даже если Алекс отрицает факт посылки подписанного сообщения, подтверждение от Кэт говорит об обратном.
В случае возникновения спорных ситуаций, например, связанных с отказом отправителя от факта подписания документа, используются услуги третьей, независимой стороны, так называемого арбитра, который расследует каждую такую ситуацию и принимает решение в пользу одной из сторон, участвующих в обмене данными.
Можно заметить, что самым критичным звеном этой схемы является именно арбитр. Во-первых, он должен быть действительно независимой ни от кого стороной. А во-вторых, арбитр должен быть абсолютно безошибочным. Ошибка в рассмотрении даже одной из нескольких тысяч спорных ситуаций подорвет доверие не только к арбитру, но и ко всем предыдущим подписанным документам, достоверность которых удостоверялась арбитром.
Именно поэтому, несмотря на теоретическую возможность применения симметричных криптосистем, на практике для выработки подписи они не используются, поскольку требуют дорогостоящих и громоздких мероприятий по поддержанию достаточного уровня достоверности передаваемых данных.
В Российской Федерации установлен государственный стандарт (ГОСТ 28147—89) на алгоритмы криптографического преобразования информации в ЭВМ, вычислительных комплексах и вычислительных сетях. Эти алгоритмы допускается использовать без ограничений для шифрования информации любого уровня секретности. Алгоритмы могут быть реализованы аппаратными и программными способами.
Стандартом определены следующие алгоритмы криптографичского преобразования информации:
• простая замена;
• гаммирование;
• гаммирование с обратной связью;
• выработка имитовставки.
Общим для всех алгоритмов шифрования является использование ключа размерностью 256 бит, разделенного на восемь 32-разрядных двоичных слов и разделение исходной шифруемой двоичной последовательности на блоки по 64 бита.
Сущность алгоритма простой замены состоит в следующем. Блок из 64-х бит исходной последовательности разбивается на два двоичных слова А и В по 32 разряда. Слово А образуют младшие биты, а слово В - старшие биты блока. Эти слова подвергаются итерационной обработке с числом итераций равным i=32. Слово, находящееся на месте младших бит блока, (А на первой итерации) суммируется по mod 232 с 32-разрядным словом ключа; разбивается на части по 4 бита в каждой (4-х разрядные входные векторы); с помощью специальных узлов замены каждый вектор заменятся на другой вектор (4 бита); полученные векторы объединяются в 32-разрядное слово, которое циклически сдвигается влево на 32 разряда и суммируется по mod 2 с другим 32-разрядным словом из 64-разрядного блока (слово В на первой итерации).
После выполнения первой итерации в блоке на месте младших бит будет расположено слово В, а слева преобразованное слово А.
На следующих итерациях операции над словами повторяются.
На каждой итерации i 32-разрядное слово ключа j (всего их 8) выбирается по следующему правилу:
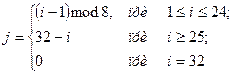
Блок замены состоит из 8 узлов замены, которые выбираются поочередно. Узел замены представляет собой таблицу из шестнадцати строк, в каждой из которых находятся векторы замены (4 бита). Входной вектор определяет адрес строки в таблице, число из которой является выходным вектором замены. Информация в таблицы замены заносится заранее и изменяется редко.
Алгоритм гаммирования предусматривает сложение по mod 2 исходной последовательности бит с последовательностью бит гаммы. Гамма получается в соответствии с алгоритмом простой замены. При выработке гаммы используются две специальные константы, заданные в ГОСТ 28147-89, а также 64-разрядная двоичная последовательность - синхропосылка. Расшифрование информации возможно только при наличии синхропосылки, которая не является секретной и может в открытом виде храниться в памяти ЭВМ или передаваться по каналам связи.








