§3. Наибольшее и наименьшее значения функции на отрезке.
При решении прикладных задач бывает нужно найти глобальные экстремумы функции на некотором промежутке. Если этот промежуток является отрезком, то экстремумы функция может достигать как в точках экстремума, так и на концах отрезка.
Пример. Найти наибольшее значение функции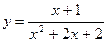 
на отрезке 
.
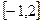Решение. Данная функция является непрерывной на данном отрезке (т.к. знаменатель не обращается в нуль), а следовательно, может принимать экстремальные значения либо в точках экстремума, либо на концах отрезка. Вычислим производную:
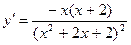. Тогда критическими точками являются точки х=0 и х=-2. Данному отрезку принадлежит только точка х=0. Вычислим значения функции в точке экстремума и на концах отрезка:
, 
, 
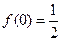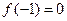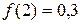. Сравнивая эти значения, заключаем, что наибольшее значение функции достигается в точке х=0.
§4. Выпуклость функции. Точки перегиба.
Опр. Функция называется выпуклой вверх (выпуклой) на промежутке Х, если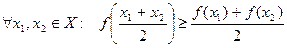 
. График выпуклой на промежутке Х функции расположен над любой ее секущей (и под любой ее касательной) на этом промежутке.
Аналогично вводится определение функции, выпуклой вниз (вогнутой).
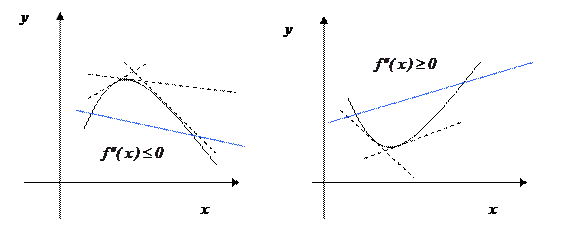
выпуклая (вверх) вогнутая (выпуклая вниз)
Теорема (критерий выпуклости функции). Пусть функция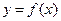 
дифференцируема в интервале (а,в). Тогда для выпуклости функции вниз необходимо и достаточно, чтобы 
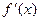монотонно возрастала на этом интервале. Для выпуклости функции вверх необходимо и достаточно, чтобы 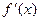монотонно убывала на этом интервале.
Следствие (достаточное условие выпуклости). Если вторая производная дважды дифференцируемой функции неотрицательна (неположительна) внутри некоторого промежутка, то функция выпукла вниз (вверх) на этом промежутке.
Опр. Точки, в которых график функции меняет направление выпуклости, называются точками перегиба графика функции.
Абсциссы точек перегиба являются точками экстремума первой производной.
Теорема (необходимое условие точки перегиба). Вторая производная дважды дифференцируемой функции в точке перегиба равна нулю: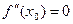 
.
Абсциссы точек, в которых выполняется необходимое условие, называются критическими точками второго рода. Если перегиб графика есть, то только в таких точках.
Теорема (достаточное условие точки перегиба). Пусть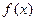 
- дважды дифференцируема в интервале (а,в). Тогда если вторая производная при переходе через критическую точку второго рода 
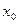меняет знак, то точка 
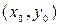является точкой перегиба графика функции.
Замечание. Если смены знака второй производной не происходит, то перегиба графика в точке нет.
Пример.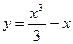 
, 
; 
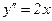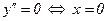- точка перегиба.
Итак, чтобы найти интервалы выпуклости функции, нужно:
1. Найти вторую производную функции.
2. Найти точки, в которых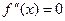 
или не существует.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод о направлении выпуклости и точках перегиба на основании достаточных условий.
§5. Асимптоты графика функции.
Графики некоторых функций расположены на плоскости так, что при неограниченном удалении от начала координат они неограниченно приближаются к некоторым прямым, но не пересекают их. Такие прямые называются асимптотами функции.
Асимптоты могут быть горизонтальными, вертикальными, наклонными.
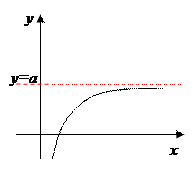
Прямая y = a называется горизонтальной асимптотой к графику функции y = f ( x ), если существует конечный предел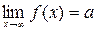 
.
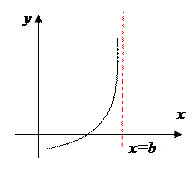
Прямая x = b называется вертикальной асимптотой к графику функции y = f ( x ), если существует конечный предел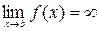 
.
Вертикальные асимптоты следует искать в точках разрыва функции или на концах области определения.
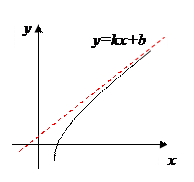
Если у функции нет горизонтальных асимптот, то, возможно, есть наклонные.
Наклонная асимптота к графику функции существует в том случае, когда существуют конечные числа к и в, вычисляемые по формулам:
, 
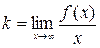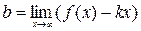. Тогда наклонная асимптота задается уравнением y = kx + b. Если хотя бы одно из чисел к и в несобственное, то наклонных асимптот у графика функции нет.
§6. Общая схема исследования функции.
I . 1. Область определения.
2. Точки пересечения с осями координат.
3. Четность.
4. Периодичность.
5. непрерывность.
6. Асимптоты.
II . 7. Монотонность.
8. Точки экстремума, экстремумы.
III . 9. Направления выпуклости.
10. Точки перегиба графика.
IV.11. Дополнительные точки.
12. Построение графика.