13. Общая характеристика нелинейных процессов переменного тока и методы их расчета
13.1 Особенности периодических процессов в нелинейных электрических цепях
В цепях переменного тока у нелинейных элементов обнаруживается ряд дополнительных особенностей, связанных с частотой воздействующих колебаний.
В достаточно широком диапазоне частот многие нелинейные элементы являются безынерционными: их нелинейная характеристика выражает зависимость между мгновенными значениями тока и напряжения. Если к такому нелинейному элементу подвести синусоидальное напряжение, то вследствие нелинейности характеристики ток будет несинусоидальным. В свою очередь, если через нелинейный элемент будет проходить синусоидальный ток, то напряжение на нем будет несинусоидальным.
Следовательно, нелинейный элемент обладает способностью преобразовывать спектр воздействующих на него колебаний; в токе появляются гармонические составляющие, которые в приложенном напряжении отсутствуют, а в другом случае в напряжении появляются гармонические составляющие, отсутствующие в токе.
Для инерционных элементов зависимость 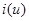 между мгновенными значениями тока и напряжения сохраняется линейной; зависимость же
между мгновенными значениями тока и напряжения сохраняется линейной; зависимость же 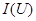 между действующими значениями тока и напряжения будет нелинейной. К их числу относятся, например, электрические лампы накаливания, бареттеры и различные терморезисторы.
между действующими значениями тока и напряжения будет нелинейной. К их числу относятся, например, электрические лампы накаливания, бареттеры и различные терморезисторы.
13.2 Метод эквивалентных синусоид
При анализе безынерционных элементов можно воспользоваться приближенным методом, основанным на замене действительных несинусоидальных кривых тока и напряжения эквивалентными им синусоидами. Соответственно такой метод можно назвать методом эквивалентных синусоид.
Другое название метода – метод эквивалентной линеаризации, поскольку в этом случае нелинейный элемент заменяется линейным. Такой метод используется для систем, имеющих относительно малую нелинейность, т.е. вклад высших гармоник невелик.
Основная задача здесь – найти выражение (или значение) нелинейного эквивалентного элемента.
Замена нелинейного элемента линейным может быть осуществлена по принципу гармонического или энергетического баланса в предположении, что через оба элемента проходит одинаковый синусоидальный ток 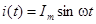
Если используется принцип гармонического баланса, то предполагается, что амплитуда основной гармоники напряжения на НЭ равна амплитуде напряжения на ЛЭ. Если используется принцип энергетического баланса, то эквивалентный ЛЭ подбирается из условия равенства активных или реактивных мощностей на выводах линейного и нелинейного элементов.
13.3 Катушка с ферромагнитным сердечником
Предположим, что к катушке с ферромагнитным сердечником приложено гармонически изменяющееся напряжение. Обычно активное сопротивление катушки невелико, и им в первом приближении можно пренебречь. Тогда приложенное напряжение будет полностью уравновешиваться противодействующей э.д.с. самоиндукции, которая является производной от потокосцепления. Поэтому магнитный поток F и потокосцепление должны также изменяться по гармоническому закону.
Пусть 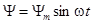 . Если пренебречь влиянием вихревых токов, то связь
. Если пренебречь влиянием вихревых токов, то связь 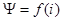 определяется петлей гистерезиса. В этом случае кривая тока в обмотке катушки содержит высшие гармоники, преимущественно третью, пятую и седьмую.
определяется петлей гистерезиса. В этом случае кривая тока в обмотке катушки содержит высшие гармоники, преимущественно третью, пятую и седьмую.
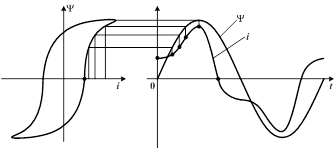
| Кривая тока 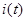 строится путем нахождения значений тока для различных значений потокосцепления Y в соответствующие моменты времени. Соединяя найденные из построения точки, получим кривую изменения тока во времени. Кривая тока несинусоидальная. строится путем нахождения значений тока для различных значений потокосцепления Y в соответствующие моменты времени. Соединяя найденные из построения точки, получим кривую изменения тока во времени. Кривая тока несинусоидальная.
|
При этом ток проходит через нуль раньше, чем потокосцепление, т.е. потокосцепление отстает по фазе от тока. Это обусловлено гистерезисом. Вихревые токи, индуктированные сердечником, вызывают еще большее отставание по фазе переменного потока от тока i.
13.4 Потери в магнитопроводах
Для правильного выбора эквивалентных синусоид, заменяющих действительные несинусоидальные кривые тока и напряжения в катушках с ферромагнитными сердечниками, необходимо рассмотреть потери энергии в сердечниках при периодическом изменении магнитного потока. Эти потери складываются из потерь на вихревые токи и на гистерезис.
Потери на вихревые токи пропорциональны квадрату частоты и квадрату амплитуды индукции. Обычно их описывают формулой
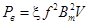 ,
,
где коэффициент x зависит от формы сечения элементов, на которые разделен сердечник, геометрических размеров этого сечения и удельной проводимости материала.
Мощность потерь на гистерезис в объеме V, обычно представляют в виде
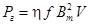
Таким образом, суммарная мощность потерь в сердечнике может быть представлена формулой
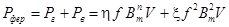
Заменим несинусоидальный ток в катушке с ферромагнитным сердечником и напряжение на ее зажимах эквивалентными синусоидами. Для этого следует выбрать амплитуды 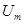 и
и 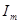 эквивалентных синусоид и угол сдвига фаз j между ними. Будем пренебрегать активным сопротивлением обмотки и индуктивным падением напряжения, определяемого потоками рассеяния. Связь между указанными величинами будем определять из условия сохранения потерь в сердечнике, т.е. из условия:
эквивалентных синусоид и угол сдвига фаз j между ними. Будем пренебрегать активным сопротивлением обмотки и индуктивным падением напряжения, определяемого потоками рассеяния. Связь между указанными величинами будем определять из условия сохранения потерь в сердечнике, т.е. из условия:
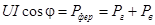
Необходимы еще два условия для определения всех трех величин. Этим условием может быть, например, соответствие 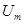 и
и 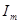 амплитудам первых гармоник напряжения и тока.
амплитудам первых гармоник напряжения и тока.
13.5 Векторная диаграмма и схема замещения катушки с ферромагнитным сердечником
Рассмотрим процессы в катушке с замкнутым ферромагнитным сердечником, обмотка которой имеет w витков.Уравнение, описывающее процесс в катушке, имеет вид
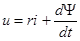 ,
,
где r — сопротивление обмотки.
Полное потокосцепление представим в виде суммы 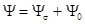 .
.
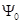 – потокосцепление, определяемое линиями магнитной индукции, замыкающимися целиком вдоль сердечника. Следовательно,
– потокосцепление, определяемое линиями магнитной индукции, замыкающимися целиком вдоль сердечника. Следовательно, 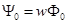 , где
, где 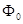 – поток сквозь сечение сердечника, определяемый этими линиями.
– поток сквозь сечение сердечника, определяемый этими линиями.
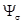 – потокосцепление, определяемое линиями магнитной индукции, замыкающимися частично или полностью в воздухе. Это потокосцепление пропорционально току:
– потокосцепление, определяемое линиями магнитной индукции, замыкающимися частично или полностью в воздухе. Это потокосцепление пропорционально току: 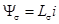 . Так как магнитное сопротивление пути, по которому замыкаются линии потока, практически не зависит от тока и, следовательно, индуктивность
. Так как магнитное сопротивление пути, по которому замыкаются линии потока, практически не зависит от тока и, следовательно, индуктивность 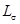 постоянна. Потокосцепление
постоянна. Потокосцепление 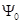 нелинейно связано с током i, так как магнитная проницаемость и, следовательно, магнитное сопротивление сердечника зависят от напряженности магнитного поля.
нелинейно связано с током i, так как магнитная проницаемость и, следовательно, магнитное сопротивление сердечника зависят от напряженности магнитного поля.
Уравнение катушки теперь можно переписать в виде:
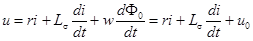 .
.
Это уравнение нелинейное. Поэтому, даже если приложенное напряжение и синусоидально, ток i будет несинусоидальным. Заменяя несинусоидальные кривые тока и потока эквивалентными синусоидами, можем записать это уравнение в комплексной форме для комплексных амплитуд:
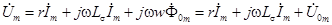 .
.
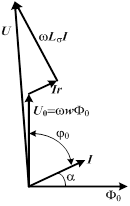
| Эквивалентная синусоида тока отстает от эквивалентной синусоиды напряжения | |
|
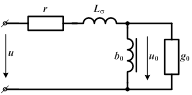
| Соответственно катушку можно представить в виде эквивалентной схемы, в которой проводимости определяют как
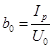 , , 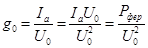 . .
| |
Процессы в такой эквивалентной цепи, распределение токов и напряжений такое же, как и в реальном устройстве.
13.6 Явление феррорезонанса
Пусть дана цепь, состоящая из последовательно соединенных реактивной катушки с ферромагнитным сердечником, линейного резистора и конденсатора. Заменим несинусоидальные кривые напряжения и тока эквивалентными синусоидами, выбрав их равными первым гармоникам реальных кривых. ВАХ катушки задана. ВАХ конденсатора и линейного резистора изображаются прямыми линиями: 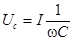 ,
, 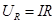 .
.
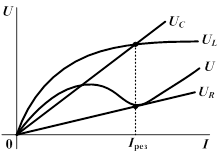
| При указанных условиях напряжение на зажимах катушки и напряжение на зажимах конденсатора по фазе противоположны друг другу. Точки, принадлежащие результирующей ВАХ схемы, получаем следующим образом: произвольно задаемся некоторым током I, находим для него разность напряжений 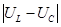 , напряжение , напряжение 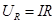 и строим результирующую кривую. и строим результирующую кривую.
|
При сравнительно малом R на результирующей ВАХ цепи имеется падающий участок, который исчезает с увеличением активного сопротивления.
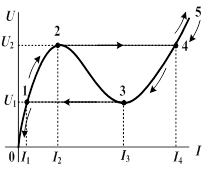
| Будем, начиная с нуля, плавно увеличивать напряжение источника э.д.с. При этом мы перемещаемся от точки 0 через точку 1 к точке 2. Если напряжение и дальше повышать, то происходит скачкообразное перемещение из точки 2 в точку 4, а затем движение будет происходить по участку 4-5. При уменьшении напряжения происходит перемещение от точки 5 через 4 к точке 3, затем произойдет скачок в точку 1 и далее от точки 1 к точке 0. |
Таким образом, при увеличении напряжения и достижении им значения 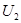 в цепи происходит скачкообразное увеличение тока со значения
в цепи происходит скачкообразное увеличение тока со значения 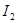 до
до 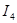 .При этом резко изменяется сдвиг фаз между током в цепи и общим напряжением: в точке 2 ток отстает от напряжения
.При этом резко изменяется сдвиг фаз между током в цепи и общим напряжением: в точке 2 ток отстает от напряжения 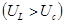 , в точке 4 ток опережает напряжение
, в точке 4 ток опережает напряжение 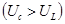 При плавном уменьшении напряжения источника э. д. с. и достижении им значения
При плавном уменьшении напряжения источника э. д. с. и достижении им значения 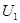 ток в цели скачком уменьшается со значения
ток в цели скачком уменьшается со значения 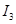 до
до 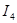 .
.
Явление резкого изменения тока в цепи при незначительном изменении напряжения на входе называют триггерным эффектом в последовательной феррорезонансной цепи.
Аналогичные процессы, наблюдаемые при параллельном соединении конденсатора и катушки со стальным сердечником, называют феррорезонансом токов.









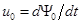 на угол
на угол 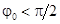 вследствие наличия потерь в сердечнике. Таким образом, эквивалентная синусоида потока
вследствие наличия потерь в сердечнике. Таким образом, эквивалентная синусоида потока 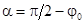 , так как эквивалентная синусоида потока
, так как эквивалентная синусоида потока 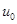 на угол
на угол 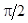 .
.