Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в узле равна нулю, .
Под узлом разветвленной магнитной цепи здесь подразумевается точка, в которой сходятся три или большее число средних линий магнитной индукции. Это понятие является условным, так как размеры поперечных сечений ветвей магнитной цепи соизмеримы с длинами ветвей. При этом под длинами ветвей магнитной цепи понимаются расстояния между соседними узлами вдоль средней линии магнитной индукции.
При этом магнитным потокам, направленным к узлу, приписывается один знак (например, положительный), а магнитным потокам, направленным от узла, – противоположный знак.
Второй закон Кирхгофа: алгебраическая сумма МДС в любом контуре равна алгебраической сумме произведений потоков на соответствующие магнитные сопротивления участков данного контура.
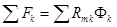
При этом необходимо задаться положительным направлением обхода контура.
Обычно рассматривают прямую и обратную задачу расчета магнитной цепи. При решении прямой задачи по заданному магнитному потоку требуется найти МДС. Соответственно, при решении обратной задачи надо по заданной величине МДС найти поток.
12. 4 Расчет разветвленных магнитных цепей
В разветвленной магнитной цепи может существовать несколько магнитных потоков, которые складываются или вычитаются на некоторых участках. Магнитодвижущие силы в этом случае аналогичны э. д. с. электрической цепи, а разность магнитных потенциалов между концами участков аналогична напряжениям между концами ветвей электрической цепи. В результате каждая магнитная цепь может представлена в виде, подобном электрической цепи.
В некоторых случаях можно произвести однократный расчет без введения эквивалентной электрической цепи. Например, в следующей схеме на участке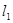 
предполагается заданным магнитный поток 
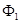и требуется определить МДС, создаваемую обмоткой.
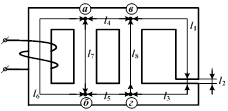
Каждый из участков имеет одинаковое сечение и одинаковую магнитную проницаемость по всей своей длине.
| 
|
Расчетные величины в этом случае определяются в следующем порядке:
разность магнитных потенциалов между точками в и г: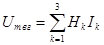 
;
напряженность магнитного поля на участке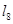 
: 
.
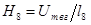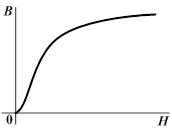
Далее по кривой намагничивания находится индукция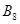 
, по которой определяется поток на этом участке 
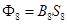, что дает возможность вычислить магнитные потоки 
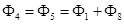и значения индукции 
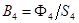и 
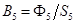. По кривой намагничивания находятся 
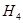и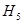 
, что позволяет вычислить разность магнитных потенциалов 
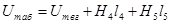. Аналогичным образом определяется 
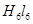и в итоге МДС: 
.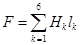