10. Анализ переходных процессов в линейных электрических цепях операторным методом
10.1 Основные положения
При использовании операторного метода действительные функции времени, называемые оригиналами, заменяются их операторными изображениями. Соответствие между оригиналом и изображением устанавливается с помощью некоторого функционального преобразования. Это преобразование выбирается так, чтобы операции дифференцирования и интегрирования оригиналов заменялись алгебраическими операциями над их изображениями. При таком подходе дифференциальные уравнения для оригиналов переходят в алгебраические уравнения для их изображений. Связь между оригиналом f(t) и его изображением F(p) устанавливается с помощью интеграла Лапласа:
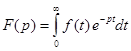, где p=s+j.
Полученное соотношение называется прямым преобразованием Лапласа. С его помощью находят операторное изображение F(p) оригинала f(t). Связь между оригиналом и изображением условно записывается так: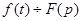 
10.2 Операторные изображения простейших функций
Из основных свойств определенных интегралов вытекают два важных следствия для изображений. Если известны изображения нескольких функций, например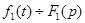 
, 
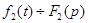и т.д., то 
,
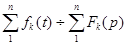т. е, изображение суммы функций равно сумме их изображений.
При a=const, соответственно, имеем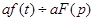 
,
т. е. при умножении функции, на постоянную величину изображение функции должно быть умножено на эту величину.
Изображение постоянной во времени функции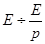 
.
Изображение показательной функции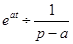 
.
Из этого соотношения могут быть найдены изображения следующих функций:
, 
.
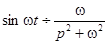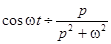10.3 Изображения производной и интеграла функции
Если известны начальное значение f(0) функции f(t) и ее изображение F(р), то изображение производной f ¢(t) можно получить, интегрируя по частям: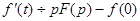 
.
Изображение второй производной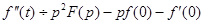 
.
Изображение напряжения на катушке: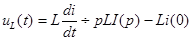 
.
Изображение неопределенного интеграла:
.
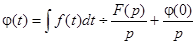Изображение напряжения на конденсаторе:
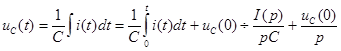
10.4 Законы электрических цепей в операторной форме
Пусть цепь с последовательным соединением r, L, С при ненулевых начальных условиях включается на напряжение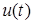 
. Тогда
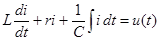
Применим к этому уравнению изображение Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений:
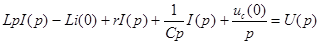
В результате вместо интегро-дифференциального уравнения получаем алгебраическое, откуда ток в такой цепи есть:
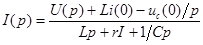
Это выражение представляет собой аналог закона Ома в операторной форме для переходного процесса при ненулевых начальных условиях. В знаменателе стоит операторное сопротивление: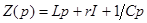 
В общем случае сложной цепи ее операторное сопротивление имеет вид:
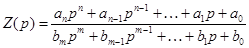
Первый закон Кирхгофа в операторном виде: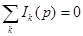 
Второй закон Кирхгофа в операторном виде при нулевых начальных условиях и отсутствии взаимной индукции имеет вид:
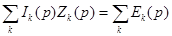
При составлении операторных уравнений удобнее использовать операторные схемы замещения, которые составляются на основе заданной электрической схемы для оригиналов. Сопротивления элементов ветвей записываются в операторной форме: R, pL, 1/pC. Изображения заданных ЭДС и токов находят, как правило, по таблицам. Ненулевые начальные условия учитывают введением дополнительных источников ЭДС (внутренних ЭДС). Полученную операторную схему рассчитывают по законам Кирхгофа в операторной форме или любым другим методом, используемым при расчете цепей постоянного тока.
10.5 Последовательность расчета операторным методом
Расчет переходных процессов в сложных цепях операторным методом состоит из двух основных этапов:
1) составления изображения искомой функции времени.
Для этого записываются законы Кирхгофа и соответствующая им алгебраическая система уравнений для изображений. При этом необходимо учесть ненулевые начальные условия. Решение системы дает изображения искомых токов и напряжений. Эти изображения имеют вид рациональных дробей.
2) переход от изображения к функции времени.
Для перехода от изображений к оригиналам можно использовать таблицы, приведенные в справочниках или, в случае сложного вида функции воспользоваться теоремой разложения.
10.6 Теорема разложения
В большинстве случаев изображение представляет собой правильную дробь:
,
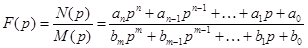у которой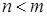 
.
Если полином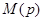 
не имеет кратных корней, то такая дробь может быть разложена на простые дроби:
,
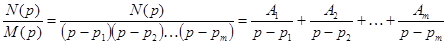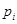- корни уравнения 
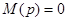, коэффициенты Ak: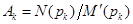 
Тогда для оригиналов можно записать следующее выражение:
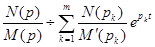
Это и есть теорема разложения, позволяющая по изображению в виде рациональной дроби найти оригинал. Если при этом один из корней 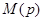равен нулю, соответствующая показательная функция превращается в постоянную величину.