8. Периодические несинусоидальные напряжения и токи в линейных цепях
8.1 Разложение периодических функций в ряд Фурье
Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. Явления, происходящие в линейных цепях при периодических, несинусоидальных напряжениях и токах проще всего поддаются исследованию, если кривые напряжения или тока разложить в тригонометрический ряд Эйлера - Фурье.
Как известно из курса математики, всякую периодическую функцию 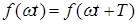 с периодом
с периодом 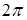 , удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Этот ряд состоит из суммы постоянной составляющей А0 (нулевая гармоника) и синусоид разных частот (гармоник)
, удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Этот ряд состоит из суммы постоянной составляющей А0 (нулевая гармоника) и синусоид разных частот (гармоник) 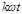 .
.
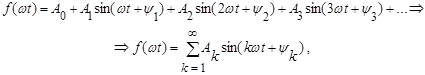 (*)
(*)
где k – целые числа, начиная с единицы, 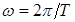 - основная частота, Т - период функции.
- основная частота, Т - период функции.
Здесь составляющая 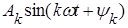 при k = 1 носит название первой гармоники, все остальные члены вида
при k = 1 носит название первой гармоники, все остальные члены вида 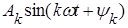 при k > 1 носят название высших гармоник. Гармоники для которых k - нечетное число, называются нечетными, а для которых k - четное число, называются четными.
при k > 1 носят название высших гармоник. Гармоники для которых k - нечетное число, называются нечетными, а для которых k - четное число, называются четными.
Суммы синусов с вспомогательными углами 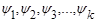 можно представить рядом Фурье, имеющим следующую форму:
можно представить рядом Фурье, имеющим следующую форму:
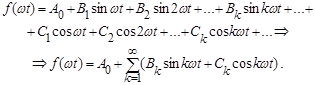 (**)
(**)
Здесь 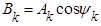 ;
; 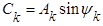 .
.
Коэффициенты 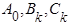 могут быть вычислены при помощи следующих интегралов:
могут быть вычислены при помощи следующих интегралов:
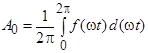 ;
; 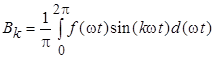 ;
; 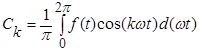 .
.
Постоянная составляющая 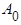 равна среднему значению функции
равна среднему значению функции 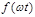 за ее период
за ее период 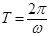 .
.
Зная коэффициенты ряда (**) можно перейти к форме (*), вычисляя
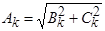 и
и 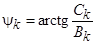 .
.
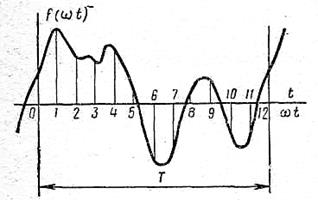
В том случае, если периодическая функция задана не аналитически, а в виде графической кривой, то при разложении ее в ряд Фурье коэффициенты ряда можно отыскать приближенно, заменяя интегралы суммой. В этом случае период Т кривой на графике разбивают на n равных частей, после чего коэффициенты 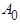 ,
, 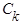 ,
, 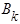 находят из выражений, где вместо
находят из выражений, где вместо 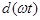 следует подставить
следует подставить 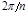 .
.
| 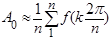 ; ;
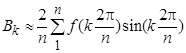 ; ; 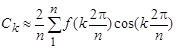 . .
|
8.2 Действующие значения напряжения и тока при несинусоидальных формах
Действующее значение несинусоидальной величины 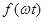 за период определяется выражением:
за период определяется выражением:
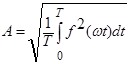 .
.
Если кривая разложена в тригонометрический ряд, то ее действующее значение можно представить в виде:
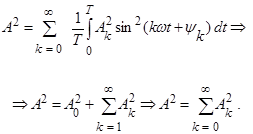
Или
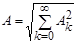 .
.
Если напряжение u состоит из ряда гармоник, действующее значение которых 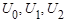 и т.д., то действующее напряжение запишется в виде:
и т.д., то действующее напряжение запишется в виде:
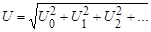 .
.
Аналогично для тока:
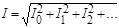 .
.
8.3 Мощность периодических несинусоидальных напряжений и токов
Активная мощность периодических функций напряжения и тока произвольной формы определяется как средняя мощность за период:
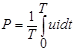 .
.
Если напряжение и ток состоят из ряда гармонических составляющих, то под знаком интеграла окажется сумма произведений гармонических равных частот:
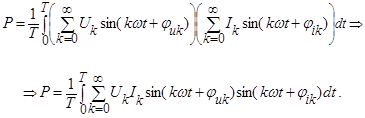
После интегрирования приходим к следующему результату:
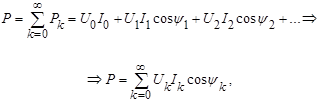
где 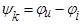 .
.
Здесь постоянные составляющие 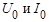 рассматриваются как гармонические составляющие с нулевой частотой.
рассматриваются как гармонические составляющие с нулевой частотой.
Аналогично реактивная мощность определится как сумма реактивных мощностей отдельных гармоник:
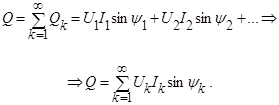
Полная мощность определится как произведение действующих значений напряжения и тока:
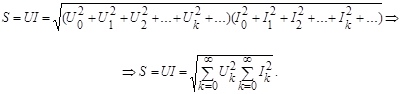
Для несинусоидальных функций в отличие от синусоидальных квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей 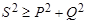 , поэтому вводят еще один вид мощности, которую называют мощностью искажения, определяемую из соотношения:
, поэтому вводят еще один вид мощности, которую называют мощностью искажения, определяемую из соотношения:
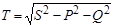 .
.
9. АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ КЛАССИЧЕСКИМ МЕТОДОМ
9.1 Общие сведения
Под переходным процессом понимают процесс перехода от одного режима работы электрической цепи (обычно периодического) к другому (обычно также периодическому), чем-либо отличающемуся от предыдущего, например, амплитудой, фазой, формой или частотой действующей в схеме э.д.с., значениями параметров схемы, а также вследствие конфигурации цепи.
Физически переходные процессы представляют собой переход от одного энергетического состояния, соответствующего докоммутационному режиму, к другому энергетическому состоянию, соответствующему послекоммутационному режиму.
Энергия магнитного поля, создаваемого током i, протекающим через индуктивность L: 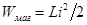
Энергия электрического поля, возникающего вследствие того, что к конденсатору емкостью C приложено напряжение 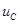 :
: 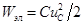 .
.
Энергии электрического и магнитного полей не могут меняться скачком на конечную величину за бесконечно малый промежуток времени, поэтому не могут меняться скачком ток в цепи с индуктивностью и напряжение на конденсаторе.
Тем самым, мы получаем два закона коммутации:
1. Ток через индуктивный элемент L непосредственно до коммутации равен току через этот же индуктивный элемент после коммутации, что принято записывать следующими образом: 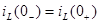 (момент времени непосредственно до коммутации и непосредственно после).
(момент времени непосредственно до коммутации и непосредственно после).
2. Напряжение на конденсаторе непосредственно до коммутации равно напряжению на этом конденсаторе после коммутации: 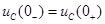 .
.
Для расчета переходных процессов в цепях составляется система уравнений по законам Ома и Кирхгофа для мгновенных значений напряжений и токов. Эта система приводится к одному уравнению для одного из напряжений или токов. Поскольку мы будем пока рассматривать линейные цепи, то итоговое уравнение будет линейным дифференциальным уравнением. Порядок этого уравнения равен числу независимых начальных условий для токов индуктивностей и напряжений на емкостях.
Решение линейных дифференциальных уравнений с постоянными коэффициентами представляет собой сумму частного решения неоднородного уравнения 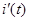 и общего решения однородного уравнения
и общего решения однородного уравнения 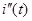 . Т.о,
. Т.о, 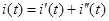
Частное решение неоднородного уравнения определяется видом функции, стоящей в правой части уравнения, и поэтому называется вынужденным. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников энергии вынужденное решение совпадает с установившимися значениями искомых величин. Оно может быть найдено теми способами расчета, которые вы рассматривали в прошлом семестре.
Общее решение i " однородного уравнения описывает процесс, происходящий без воздействия внешних источников за счет изменения запаса энергии, накопленной в цепи до начала переходного процесса; оно имеет одинаковый вид для любого переходного процесса в данной цепи. Это решение называют свободной составляющей переходного процесса.
Решение однородного дифференциального уравнения ищется в виде
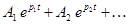 ,
,
где 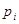 – корни характеристического уравнения.
– корни характеристического уравнения.
Постоянные интегрирования 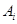 , входящие в выражение для переходной величины, определяют из начальных условий – значений напряжений на емкостях и токов в индуктивностях, которые в соответствии с законами коммутации не могут изменяться скачком.
, входящие в выражение для переходной величины, определяют из начальных условий – значений напряжений на емкостях и токов в индуктивностях, которые в соответствии с законами коммутации не могут изменяться скачком.
9.2 Переходные процессы в цепи с одним реактивным элементом
Здесь приведены примеры задач с индуктивным элементом, аналогичные задачи могут быть рассмотрены и для цепей с емкостным элементом.
1. Короткое замыкание цепи
Рассмотрим следующую цепь.
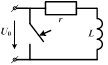
| При коротком замыкании цепи с последовательным соединением r и L уравнение переходного тока i, равного в этом случае свободному току i", имеет вид:
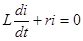
|
Характеристическое уравнение 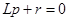 имеет корень
имеет корень 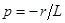 , тогда
, тогда
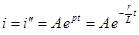
Если до момента короткого замыкания по цепи шел постоянный ток 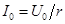 , где
, где 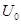 – постоянное напряжение цепи, это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования:
– постоянное напряжение цепи, это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования: 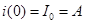 .
.
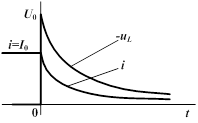
| Следовательно, 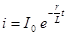 , ,
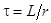 называется постоянной времени.
В цепи появляется э. д. с. самоиндукции: называется постоянной времени.
В цепи появляется э. д. с. самоиндукции:
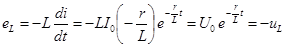 . .
|
Энергия, расходуемая на нагрев сопротивления r цепи за время переходного процесса равна энергии, запасенной в индуктивности до замыкания цепи:
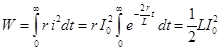
2. Включение цепи на постоянное напряжение
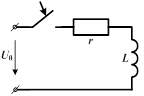
| При включении цепи r , L на постоянное напряжение 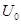 вынужденный ток вынужденный ток 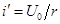 , а переходный ток , а переходный ток
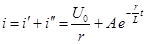 . .
|
Ток до переходного процесса, а следовательно, и в первый момент после включения равен нулю:
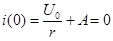 ,
,
откуда 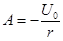 и
и 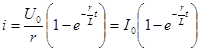 ,
,
т. е. переходный ток постепенно нарастает до своего окончательного значения 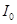 и тем медленней, чем больше постоянная времени t.
и тем медленней, чем больше постоянная времени t.
Напряжения на участках цепи
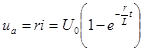 ;
; 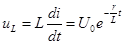
Следовательно, в первый момент напряжение цепи целиком сосредоточивается на индуктивности и затем постепенно переходит на сопротивление.
3. Включение цепи на синусоидальное напряжение
Пусть цепь r , L включается на синусоидальное напряжение 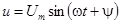 . Тогда значение напряжения в момент включения
. Тогда значение напряжения в момент включения 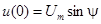 определяется величиной начальной фазы y, которая в этом случае называется также фазой включения.
определяется величиной начальной фазы y, которая в этом случае называется также фазой включения.
Вынужденный ток (в случае активно-индуктивного характера цепи ток отстает от напряжения):
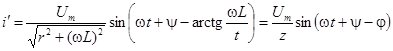
Переходный ток: 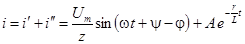 .
.
Учет начального условия дает: 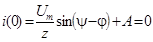 Þ
Þ 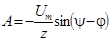
и окончательно 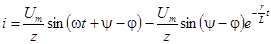 .
.
Переходное напряжение на активном сопротивлении пропорционально току, а на индуктивности есть
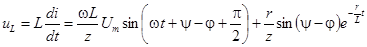 .
.
При включении в момент времени, когда вынужденный ток равен нулю, например при 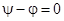 , уравнения принимают вид
, уравнения принимают вид
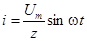 и
и 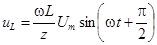 ,
,
т. е. свободного тока и свободных напряжений на участках цепи нет, и сразу после включения наступает установившийся процесс.
В общем же случае на синусоидальные установившиеся напряжения на участках цепи и ток налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток i и напряжения 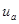 и
и 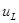 в течение некоторых промежутков времени могут превосходить их максимальные значения
в течение некоторых промежутков времени могут превосходить их максимальные значения 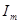 ,
, 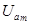 и
и 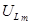 при установившемся режиме. В результате может возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения y и от постоянной времени t, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
при установившемся режиме. В результате может возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения y и от постоянной времени t, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
Так, при включении в момент времени, когда вынужденный ток получает максимальное значение 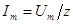 , например при
, например при 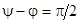 ,
,
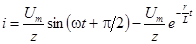 ;
; 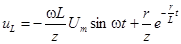
При большой постоянной времени получается большой сверхток, однако он не может превзойти двойную амплитуду 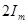 установившегося тока.
установившегося тока.
9.3 Переходные процессы в линейных электрических цепях с двумя реактивными элементами
Рассмотрим характер этих процессов на примере короткого замыкания цепи с последовательным соединением индуктивности и емкости.
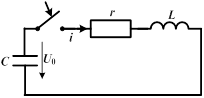
| Пусть емкость, заряженная до напряжения 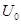 , замыкается на цепь с последовательным соединением сопротивления и индуктивности. Тогда уравнение по второму закону Кирхгофа будет однородным: , замыкается на цепь с последовательным соединением сопротивления и индуктивности. Тогда уравнение по второму закону Кирхгофа будет однородным: 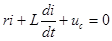 , откуда , откуда 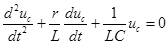 . .
|
Характеристическое уравнение 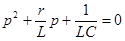 имеет два корня:
имеет два корня:
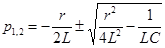 .
.
Если 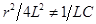 т.е.
т.е. 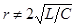 , корни будут различными
, корни будут различными 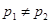 .
.
В этом случае решение дифференциального уравнения 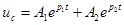 , а ток в цепи
, а ток в цепи 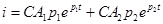
В момент t = 0 напряжение на емкости и ток индуктивности, равный току всей цепи, будут такими же, как и до замыкания:
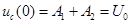 ,
, 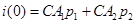
откуда постоянные интегрирования 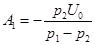 ,
, 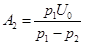
и, следовательно, ток и напряжения на участках будут:
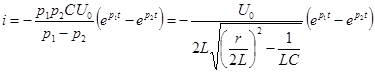 ;
; 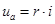 ;
;
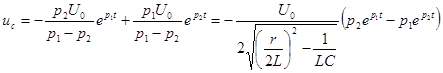 ;
;
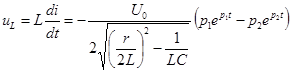
Характер переходного процесса зависит от соотношения между параметрами r , L и С.
1. Если 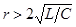 , корни
, корни 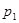 и
и 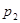 будут вещественными, причем
будут вещественными, причем 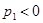 ,
, 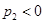 ,
, 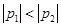 .
.
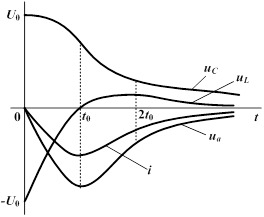
| Напряжение конденсатора, начиная с 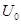 , непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение на сопротивлении, начинаясь с нуля, всегда отрицательны, что соответствует току разряда. Напряжение , непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение на сопротивлении, начинаясь с нуля, всегда отрицательны, что соответствует току разряда. Напряжение 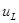 на индуктивности возникает скачком, принимая значение на индуктивности возникает скачком, принимая значение 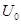 ; проходит через нуль в момент ; проходит через нуль в момент 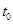 при равенстве значений своих экспонент, т.е. при при равенстве значений своих экспонент, т.е. при 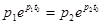 ,откуда ,откуда 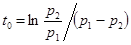 и затем становится положительным. и затем становится положительным.
|
Так как 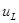 пропорционально производной от тока, то в момент времени
пропорционально производной от тока, то в момент времени 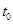 абсолютное значение тока проходит через максимум. Приравняв производную
абсолютное значение тока проходит через максимум. Приравняв производную 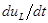 нулю, можно видеть, что
нулю, можно видеть, что 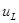 имеет максимум при
имеет максимум при 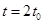 .
.
Рассмотренный вид разряда называется апериодическим.
2. Пусть 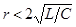 .
.
Введем обозначения: 
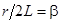 ,
, 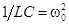 ,
, 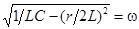 .
.
Тогда выражение для корней характеристического уравнения можно переписать следующим образом:
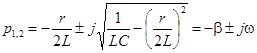
Так как w – число вещественное, корни 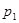 и
и 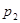 будут комплексными. После подстановки значений
будут комплексными. После подстановки значений 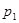 и
и 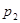 выражения для тока и напряжений на участках примут вид:
выражения для тока и напряжений на участках примут вид:
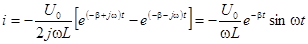 ,
, 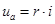 ,
,
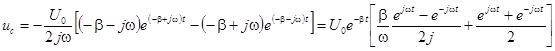 .
.
Обозначим 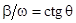
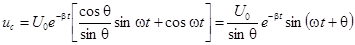 .
.
Аналогично
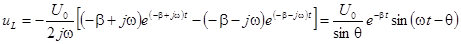 .
.
Ток и напряжения цепи, в которой 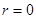 и, следовательно,
и, следовательно, 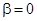 ,
, 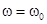 ,
, 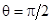 :
:
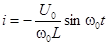 ,
, 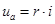 ,
,  ,
, 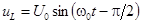 .
.
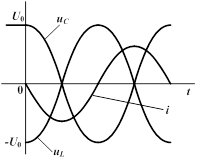
Следовательно, если бы в цепи не происходило рассеяние энергии, ток и напряжения на участках были бы синусоидальными функциями времени, т.е. имели бы место собственные незатухающие колебания, угловая частота которых равна резонансной частоте этой цепи 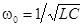 . Для незатухающих колебаний векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости аналогичны тем, которые имеют место при резонансе в цепи с последовательным соединением r , L и С. Следовательно, и здесь происходит полный обмен энергиями между С и L. . Для незатухающих колебаний векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости аналогичны тем, которые имеют место при резонансе в цепи с последовательным соединением r , L и С. Следовательно, и здесь происходит полный обмен энергиями между С и L.
| 
|
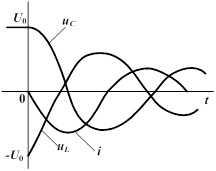
| Если в цепи есть сопротивление 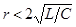 , разряд также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как , разряд также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как 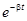 с ростом t стремится к нулю. Угловая частота этих собственных затухающих колебаний с ростом t стремится к нулю. Угловая частота этих собственных затухающих колебаний 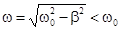 . Энергетический процесс заключается в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда запасенная энергия полностью рассеется. . Энергетический процесс заключается в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда запасенная энергия полностью рассеется.
|
3. Если 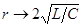 , частота
, частота 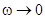 и в выражении для тока возникает неопределенность:
и в выражении для тока возникает неопределенность: 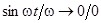 . Такой режим разряда называется критическим.
. Такой режим разряда называется критическим.
Раскрывая неопределенность 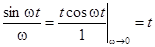 , для этого случая получаем:
, для этого случая получаем:
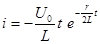 ,
, 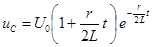 ,
, 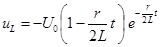 .
.
Характер разряда будет апериодическим.








