Рассмотрим несимметричную трехфазную цепь с неравномерной нагрузкой, соединенной в «треугольник».
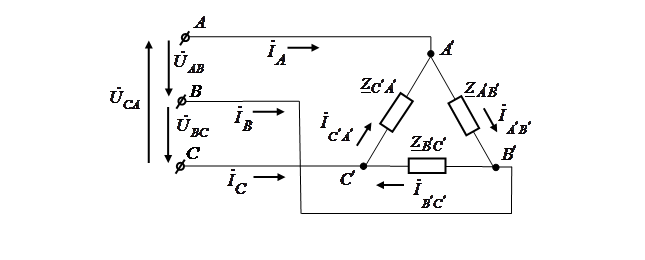
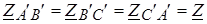 .
.
При соединении «треугольником» линейные напряжения равны фазным, а линейные токи равны разности соответствующих фазных токов: 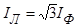 ;
; 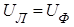 ;
;
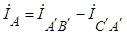 ;
; 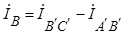 ;
; 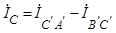 ; .
; .
Токи в фазах приемника: 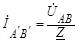 ;
; 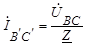 ;
; 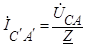 .
.
В симметричной системе выполняется равенство:
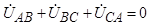 .
.
Расчет трехфазных систем выполняют с применением комплексных амплитуд. При расчете используются все рассмотренные ранее методы анализа линейных электрических цепей (узловых напряжений, контурных токов, преобразования схем).
Преобразование трехфазной цепи со смешанной нагрузкой
К преобразованию схемы следует прибегать в том случае, когда цепь включает в себя несколько приемников, имеющих различные схемы соединений. Рассмотрим трехфазную цепь:
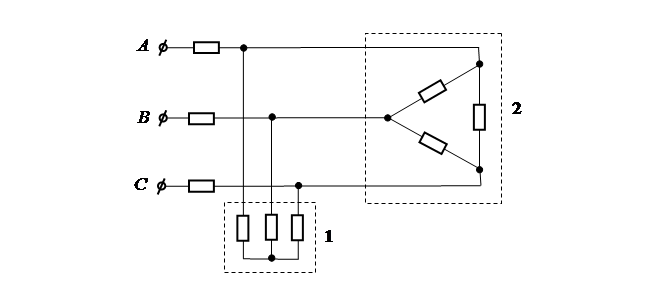
При расчете токов в приведенной схеме звезду 1 следует преобразовать в эквивалентный треугольник, ветви которого будут параллельны ветвям треугольника 2. В этом случае получим эквивалентную схему.
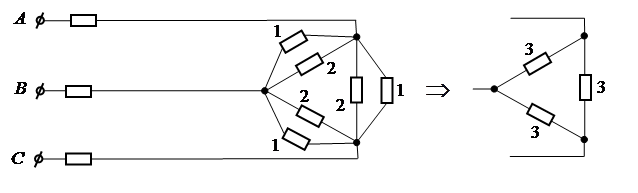
Полученную трехфазную цепь рассчитывают по приведенным выше формулам.
6.4 Энергия и мощность в трехфазных цепях
В трехфазной системе с нулевым проводом активная мощность складывается из активных мощностей фаз нагрузки (РА, РВ, РС), потерь в линии ( 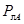 ,
, 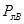 ,
, 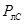 ) и нейтральном проводе
) и нейтральном проводе 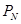 :
:
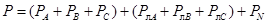 .
.
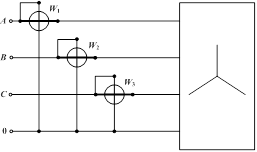
Для измерения активной мощности в трехфазной цепи с нейтральным проводом необходимо включить три ваттметра.
|
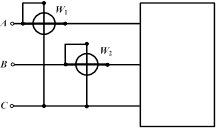
Если нулевой провод отсутствует, то измерение активной мощности можно осуществить двумя ваттметрами.
|
При измерении мощностей в симметричной системе достаточно измерить мощность, потребляемую одной фазой. Активная мощность при симметричной нагрузке
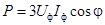 ,
,
где φ – угол между напряжением и током в фазе нагрузки.
7. ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ
7.1 Уравнения четырехполюсников
Электрическая цепь, имеющая два входных и два выходных зажима, называется четырехполюсником.
Активные четырехполюсники содержат внутри себя также источники электрической энергии. Соответственно, пассивные четырехполюсники внутри себя источников энергии не содержат. Примером их могут служить линия передачи, трансформатор, мостовая схема.
Принято изображать 4-полюсник в виде прямоугольника с двумя парами зажимов.
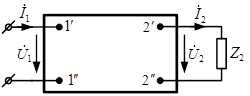
| 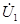 и и 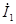 – комплексные напряжение и ток на входе четырехполюсника, – комплексные напряжение и ток на входе четырехполюсника, 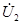 и и 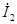 – комплексные напряжение и ток на его выходе, – комплексные напряжение и ток на его выходе, 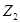 – комплексное сопротивление нагрузки. – комплексное сопротивление нагрузки.
|
Для вывода уравнений, связывающих входные и выходные напряжения и токи, удобно заменить приемник 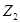 с напряжением
с напряжением 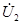 эквивалентным источником напряжения без внутреннего сопротивления с ЭДС равной
эквивалентным источником напряжения без внутреннего сопротивления с ЭДС равной 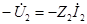 .
.
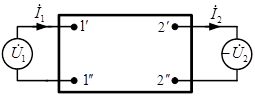
| Применим метод наложения. Сначала учитываем только источник 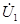 . Замыкая накоротко зажимы источника . Замыкая накоротко зажимы источника 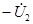 , находим токи , находим токи 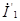 и и 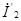 , которые, будут пропорциональны напряжению , которые, будут пропорциональны напряжению 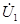 : :
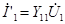 , , 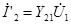
|
Аналогично, при наличии источника 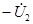 и коротком замыкании
и коротком замыкании 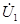 :
:
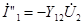 ,
, 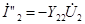
Здесь 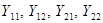 –комплексные коэффициенты пропорциональности, имеющие размерность проводимости;
–комплексные коэффициенты пропорциональности, имеющие размерность проводимости; 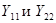 называются входными, a
называются входными, a 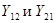 взаимными проводимостями. Проводимости
взаимными проводимостями. Проводимости 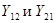 определяют токи в короткозамкнутом выходном или входном контуре при заданном напряжении в другом контуре.
определяют токи в короткозамкнутом выходном или входном контуре при заданном напряжении в другом контуре.
При одинаковом напряжении U токи 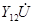 и
и 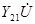 по принципу взаимности были бы равны между собой. Следовательно, взаимные проводимости:
по принципу взаимности были бы равны между собой. Следовательно, взаимные проводимости: 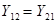 .
.
Действительные токи на входе и выходе четырехполюсника
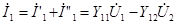 и
и 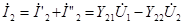 .
.
Совместное решение этих уравнений дает
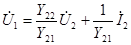 ,
,
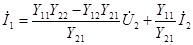 .
.
После введения обозначений
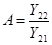 ,
, 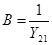 ,
, 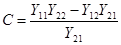 и
и 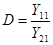
получаются уравнения четырехполюсника:
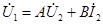 ,
, 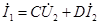
где комплексы А, В, С, D называются параметрами четырехполюсника. Между ними существует следующая связь:
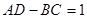 .
.
Следовательно, из четырех параметров независимыми являются три.
В симметричном четырехполюснике, который со стороны выходных зажимов представляет ту же цепь, что и со стороны входных,
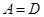 и
и 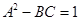 .
.
С помощью уравнений четырехполюсника можно определить нагрузочный режим, т. е. найти 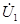 и
и 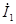 для заданных
для заданных 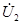 и
и 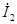 или две любые величины из указанных, если заданы две другие.
или две любые величины из указанных, если заданы две другие.
7.2 Холостой ход и короткое замыкание четырехполюсника
При холостом ходе ток на выходе 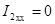 и уравнения четырехполюсника дают
и уравнения четырехполюсника дают 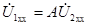 ,
, 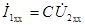 .
.
При коротком замыкании напряжение на выходе 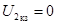 и из уравнений четырехполюсника вытекает, что
и из уравнений четырехполюсника вытекает, что 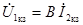 ,
, 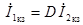 .
.
Отсюда видно, что параметр A представляет собой отношение входного и выходного комплексных напряжений при холостом ходе четырехполюсника, a D – отношение входного и выходного комплексных токов при коротком замыкании.
Если при холостом ходе напряжение на выходе будет равно напряжению 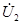 при нагрузке, а при коротком замыкании ток на выходе – току
при нагрузке, а при коротком замыкании ток на выходе – току 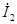 при нагрузке, уравнения четырехполюсника получают вид:
при нагрузке, уравнения четырехполюсника получают вид:
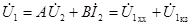 ,
, 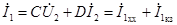
Следовательно, напряжение 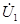 и ток
и ток 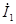 при любом заданном режиме работы приемника (
при любом заданном режиме работы приемника ( 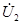 и
и 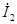 ) могут быть определены путем наложения соответствующих режимов холостого хода и короткого замыкания.
) могут быть определены путем наложения соответствующих режимов холостого хода и короткого замыкания.
Чтобы осуществить это наложение, надо знать, как расположить друг относительно друга векторные диаграммы холостого хода и короткого замыкания Для этой цели нужно измерить сдвиг фаз σ между векторами 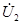 и
и 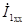 при опыте холостого хода и сдвиг фаз β между векторами
при опыте холостого хода и сдвиг фаз β между векторами 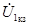 и
и 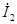 при опыте короткого замыкания.
при опыте короткого замыкания.
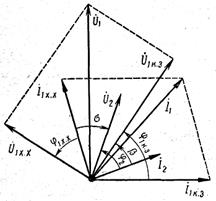
| После этого построение ведется в следующем порядке: строится заданная диаграмма 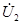 и и 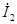 , затем под углом σ к вектору , затем под углом σ к вектору 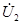 строится вектор строится вектор 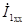 , а под углом , а под углом 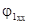 к нему вектор к нему вектор 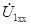 . Далее под углом β к вектору . Далее под углом β к вектору 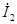 строится вектор строится вектор 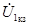 , а под углом , а под углом 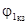 к нему – вектор к нему – вектор 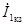 . После этого строятся векторы напряжения и тока на входе ( . После этого строятся векторы напряжения и тока на входе ( 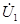 и и 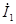 ) как суммы напряжений и токов при холостом ходе и коротком замыкании. ) как суммы напряжений и токов при холостом ходе и коротком замыкании.
|
Так как в симметричном четырехполюснике А = D , то
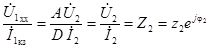
т. е. угол сдвига фаз между векторами 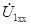 и
и 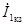 равен заданному углу φ2 сдвига фаз в нагрузке, что сразу определяет взаимное расположение векторных диаграмм холостого хода и короткого замыкания без добавочных измерений.
равен заданному углу φ2 сдвига фаз в нагрузке, что сразу определяет взаимное расположение векторных диаграмм холостого хода и короткого замыкания без добавочных измерений.
Указанное применение принципа наложения имеет большое значение при испытании мощных электротехнических устройств, описываемых линейными уравнениями, так как позволяет заменить опыт нагрузки, требующий источников большой мощности, опытами холостого хода и короткого замыкания при значительно меньшей мощности.
7.3 Определение параметров четырехполюсника
Если известны конкретная схема и сопротивления (проводимости) ветвей четырехполюсника, то его параметры могут быть определены расчетным путем по входным и взаимным проводимостям. Можно также исходить непосредственно из зависимостей, устанавливаемых законами Кирхгофа.
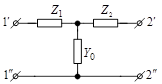
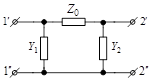
В качестве примера рассмотрим простейшие схемы четырехполюсников. Так как из четырех параметров четырехполюсника независимыми являются три, то простейшие схемы должны содержать три ветви, т. е. представлять собой соединение звездой (Т-образная схема) или треугольником (П-образная схема).
| 
|
Для Т-образной схемы при режиме холостого хода очевидны следующие соотношения:
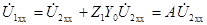 ,
, 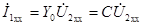 ;
;
при коротком замыкании:
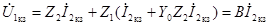 ,
, 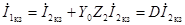
Отсюда параметры этого четырехполюсника:
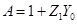 ,
, 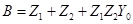 ,
, 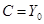 ,
, 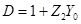
Параметры П-образной схемы могут быть определены аналогично:
при холостом ходе:
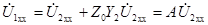 ,
, 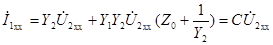 ;
;
при коротком замыкании
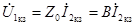 ,
, 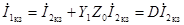
Отсюда параметры П-схемы
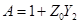 ,
, 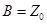 ,
, 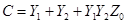 ,
, 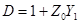
Любой сложный четырехполюсник можно заменить простейшим эквивалентным ему, т. е. Т- или П-схемой. Параметры этих эквивалентных схем выражаются через параметры четырехполюсника.
Для Т-схемы: 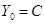 ,
, 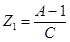 ,
, 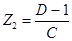 ;
;
Для П-схемы: 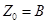 ,
, 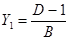 ,
, 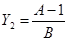 .
.
Видно, что схемы, эквивалентные симметричным четырехполюсникам, сами тоже симметричны, так как, если 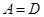 , то
, то 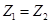 и
и 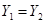 .
.
Если конкретная схема и параметры ветвей четырехполюсника неизвестны, его параметры могут быть определены из опытов холостого хода и короткого замыкания при питании и измерениях со стороны входа и со стороны выхода. Эти измерения позволяют определить комплексы сопротивлений короткого замыкания 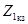 и холостого хода
и холостого хода 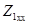 при питании схемы со стороны входных зажимов 1'-1″ и
при питании схемы со стороны входных зажимов 1'-1″ и 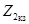 и
и 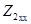 при питании схемы со стороны выходных зажимов 2' -2":
при питании схемы со стороны выходных зажимов 2' -2":
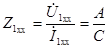 ;
; 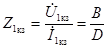 ;
;
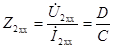 ;
; 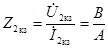 ;
;
Как видно из этих выражений, полные сопротивления при коротком замыкании и холостом ходе связаны между собой соотношением:
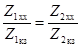 ,
,
поэтому из четырех вышеупомянутых опытов необходимы лишь три, а четвертый может служить для контроля.
Параметры четырехполюсника находят по формулам:
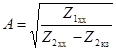 ;
; 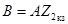 ;
; 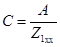 ;
; 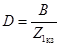 .
.








