5. Анализ процессов в цепях с индуктивной связью
5.1 Явление взаимной индукции
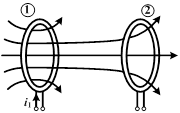
| Рассмотрим цепь, включающую в себя две катушки. При этом, магнитный поток, создаваемый током в первой катушки пересекает площадь витков второй катушки или, как принято говорить, магнитный поток сцеплен со второй катушкой. В этом случае изменение тока 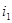 первой катушки приведет не только к появлению в ней ЭДС самоиндукции первой катушки приведет не только к появлению в ней ЭДС самоиндукции 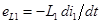 , но и к появлению во второй катушке ЭДС взаимной индукции: , но и к появлению во второй катушке ЭДС взаимной индукции: 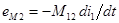 . .
|
Аналогично, изменение тока 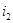 второй катушки приведет к появлению в ней ЭДС самоиндукции
второй катушки приведет к появлению в ней ЭДС самоиндукции 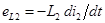 , и к появлению в первой катушке ЭДС взаимной индукции:
, и к появлению в первой катушке ЭДС взаимной индукции: 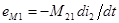 .
.
При этом можно показать, что 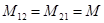 – коэффициент взаимной индукции (взаимная индуктивность).
– коэффициент взаимной индукции (взаимная индуктивность).
При рассмотрении связанных катушек вводят понятие об одноименных зажимах катушек. Зажимы двух катушек называются одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции 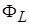 и взаимоиндукции
и взаимоиндукции 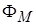 в каждой катушке совпадают по направлению. Одноименность зажимов катушек зависит от их взаимного расположения и направления намотки витков. Одну из двух пар одноименных зажимов обозначают «точками» или «звездочками».
в каждой катушке совпадают по направлению. Одноименность зажимов катушек зависит от их взаимного расположения и направления намотки витков. Одну из двух пар одноименных зажимов обозначают «точками» или «звездочками».
5.2 Последовательное и параллельное соединения индуктивно связанных катушек
При последовательном соединении катушек ток в них один и тот же, а приложенное напряжение должно преодолеть все ЭДС и сопротивления цепи.
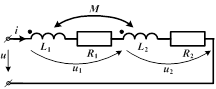
| Рассмотрим согласное включение катушек, когда магнитные потоки самоиндукции и взаимоиндукции в обеих катушках направлены одинаково. В этом случае ЭДС самоиндукции и взаимоиндукции имеют одинаковые знаки. |
Тогда приложенное напряжение при обходе контура по принятому положительному направлению тока:
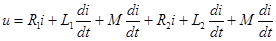 .
.
При встречном включении катушек магнитные потоки самоиндукции и взаимоиндукции направлены в противоположные стороны и ЭДС взаимоиндукции имеет знак, обратный знаку ЭДС самоиндукции. Тогда приложенное напряжение:
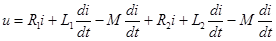
В общем виде можно записать:
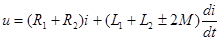 .
.
Для синусоидального напряжения и тока это же соотношение может быть записано в комплексной форме:
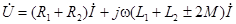 .
.
Следовательно, результирующая индуктивность всей цепи при согласном включении 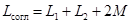 ,
,
при встречном включении 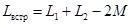
Векторные диаграммы:
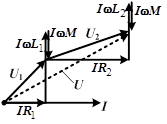
| согласное включение | встречное включение |
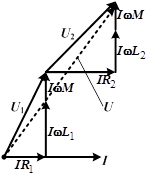
| 
|
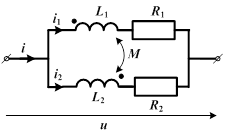
При параллельном соединении катушек их напряжение одинаково.
согласное
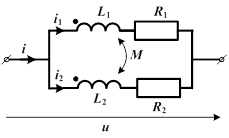
| встречное
|
Тогда выражения для напряжений на первой и второй катушках имеют вид:
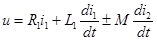 ,
, 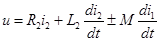 ;
;
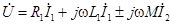 ,
, 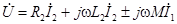 .
.
Здесь верхний знак относится к согласному включению, а нижний – к встречному.
Обозначая 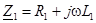 ,
, 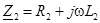 ,
, 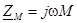 , для согласного включения можно записать:
, для согласного включения можно записать:
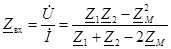 ,
,
для встречного:
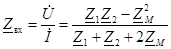 .
.
5.3 Трансформатор без стального сердечника
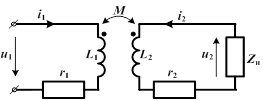
| Широкое применение в электротехнике имеет трансформатор – устройство, предназначенное для преобразования величины переменных напряжений и токов. В простейшем случае он не имеет ферромагнитного сердечника и представляет собой две катушки с индуктивной связью. |
Напряжение 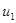 источника приложено к первичной катушке трансформатора, к вторичной катушке подключена нагрузка. Тогда уравнения по второму закону Кирхгофа для первичной и вторичной цепей при показанных на рисунке одноименных зажимах и положительных направлениях токов, при которых потоки самоиндукции и взаимоиндукции складываются, получают следующий вид:
источника приложено к первичной катушке трансформатора, к вторичной катушке подключена нагрузка. Тогда уравнения по второму закону Кирхгофа для первичной и вторичной цепей при показанных на рисунке одноименных зажимах и положительных направлениях токов, при которых потоки самоиндукции и взаимоиндукции складываются, получают следующий вид:
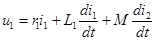 ,
,
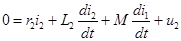 ,
,
где 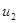 – напряжение на приемнике,
– напряжение на приемнике, 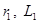 и
и 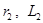 – сопротивление и индуктивность первичной и вторичной, катушек, соответственно.
– сопротивление и индуктивность первичной и вторичной, катушек, соответственно.
При холостом ходе вторичная катушка разомкнута и ток 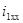 первичной цепи индуктирует во вторичной ЭДС взаимоиндукции
первичной цепи индуктирует во вторичной ЭДС взаимоиндукции 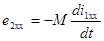 .
.
При сопротивлении приемника 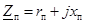 уравнения трансформатора в комплексной форме имеют вид:
уравнения трансформатора в комплексной форме имеют вид:
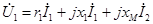 ,
,
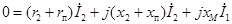 .
.
Здесь 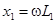 ,
, 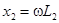 ,
, 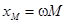 .
.
Из второго уравнения может быть определен комплекс вторичного тока:
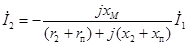 .
.
Переход от комплекса вторичного тока к его действующему значению дает:
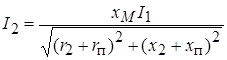 ,
,
откуда может быть определен коэффициент трансформации тока
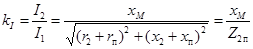 .
.
Из этих соотношений видно, что коэффициент трансформации тока не является постоянной величиной, а зависит от сопротивления приемника.
Коэффициент трансформации напряжения 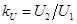 также зависит от сопротивления приемника.
также зависит от сопротивления приемника.
После подстановки значения 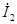 в первое уравнение трансформатора получается выражение первичного тока:
в первое уравнение трансформатора получается выражение первичного тока:
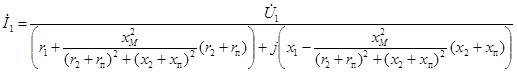 .
.
Знаменатель этого выражения представляет собой результирующее полное сопротивление цепи, эквивалентной трансформатору.








