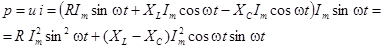3. Нахождение комплексных изображений искомых функций.
4. Переход к оригиналам этих функций.
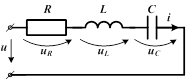
| В качестве примера рассмотрим цепь с последовательно соединенными участками R,L и C, к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону  .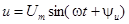
|
Требуется найти ток в цепи: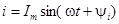 
.
1) В соответствии с алгоритмом заменяем функции времени их изображениями: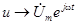 
, 
.
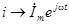2) Составляем уравнение по второму закону Кирхгофа:
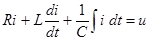и записываем его для комплексных изображений, заменив ток, его производную и интеграл их комплексными выражениями:
.
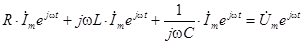Полученное уравнение уже является алгебраическим. Все слагаемые имеют одинаковый множитель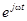 
, на который уравнение можно поделить. Окончательно получаем уравнение для комплексных амплитуд:
.
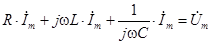Поэтому рассматриваемый метод расчета часто называют методом комплексных амплитуд. В дальнейшем сразу не будем писать множитель 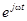, а составлять уравнение для комплексных амплитуд.
3) Из последнего уравнения легко определяется комплексная амплитуда тока:
,
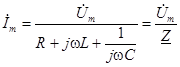где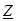 
– полное комплексное сопротивление цепи.
4) Зная выражение для комплексной амплитуды тока в виде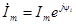 
, легко записать выражение для мгновенного тока: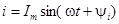
Нас обычно интересуют действующие токи и напряжения. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в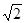 
, то обычно вместо комплексных амплитуд рассматривают комплексные действующие величины: 
, 
.
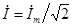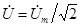Комплексные сопротивление и проводимость
Отношение комплексного напряжения к комплексному току называют комплексным сопротивлением цепи и обозначают .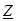
,
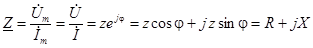где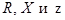 
– активное, реактивное и полное сопротивления цепи.
В частности, для последовательного соединения R,L и C
.
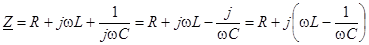Аналогично, отношение комплексного тока к комплексному напряжению называют комплексной проводимостью цепи и обозначают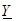 
. Имеем:
,
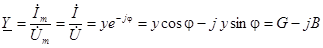где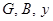 
– активная, реактивная и полная проводимости цепи.
Для параллельного соединения трех элементов
.
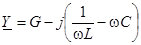Очевидно, существует связь: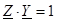 
или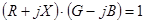 
Основные законы электрических цепей в комплексной форме
Вид законов электрических цепей переменного тока в комплексной форме такой же, как и для цепи постоянного тока. Только необходимо произвести замену соответствующих постоянных величин комплексными: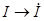 
, 
, 
, 
, 
, 
.
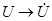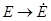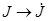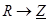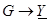Закон Ома в комплексной форме имеют вид: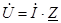 
.
Достоинство этих выражений заключается в том, что в них учитывается как связь между действующими значениями тока и напряжения, так и сдвиг фаз между ними.
Первый закон Кирхгофа в применении к узлу цепи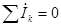 
.
Второй закон Кирхгофа применительно к контуру цепи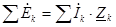 
.
Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.
При последовательном соединении участков цепи напряжение на зажимах всей цепи равняется сумме падений напряжений на отдельных участках. Следовательно, при последовательном соединении комплексное сопротивление всей цепи равно алгебраической сумме комплексных сопротивлений отдельных участков цепи: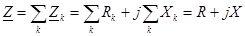 
При параллельном соединении участков цепи общий ток на входе цепи равен сумме токов в отдельных участках. Таким образом, при параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных участков цепи:
.
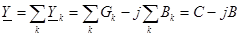При смешанном соединении:
|  ;  ,  .
 ,  ,  .
|
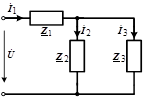
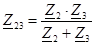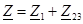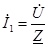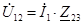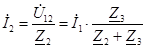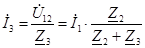Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.
4.5 Энергетические соотношения в цепях синусоидального тока
В цепях постоянного тока и напряжения мощность определялась как
.
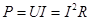В цепях синусоидального тока принято говорить о мгновенной мощности цепи.
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
