Следовательно, в цепи с емкостью С напряжение отстает от тока по фазе на 90°. .
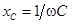 – емкостное сопротивление (тоже реактивное), учитывающее реакцию емкости на протекание переменного тока.
– емкостное сопротивление (тоже реактивное), учитывающее реакцию емкости на протекание переменного тока.
Действующие и средние значения периодических ЭДС и токов
Так как тепловое действие тока пропорционально квадрату этого тока, то о величине периодических токов и ЭДС в технике обычно судят по их средним квадратичным значениям за полный период.
Понятие о среднем квадратичном значении можно получить, рассматривая тепловое действие тока. Пусть сопротивление цепи, в которой протекает периодический ток, равно r . Тогда по закону Джоуля – Ленца количество тепла, выделяемое в этой цепи током за элементарный промежуток времени dt, будет 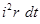 , а за каждый полный период
, а за каждый полный период 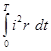 .
.
Обозначим через I такой постоянный ток, который за этот промежуток времени Т выделит в сопротивлении r такое же количество тепла. Тогда имеем:
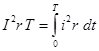 , откуда
, откуда 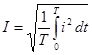 .
.
Величина I, определяемая последним равенством, называется действующим или средним квадратичным значением периодического тока.
Для синусоидального тока имеем: 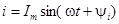 и, следовательно,
и, следовательно,
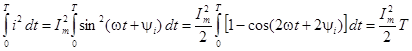 .
.
так интеграл от второго слагаемого равен нулю. Окончательно для действующего значения синусоидального тока получим
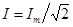 .
.
Аналогично определяется действующее значение Е периодической ЭДС:
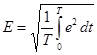 .
.
Для действующего значения синусоидальной ЭДС: 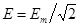 .
.
Приборы, применяемые для измерения периодических ЭДС и токов, обычно дают их действующие значения.
Кроме средних квадратичных значений периодических ЭДС и токов, используют их средние арифметические значения.
Под средними арифметическими или просто средними значениями ЭДС и тока за промежуток времени от t1 до t2 понимают, соответственно, величины:
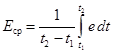 и
и 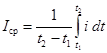 .
.
Для синусоидальных ЭДС и токов среднее значение за полный период равно нулю, так как площади положительной и отрицательной полуволн синусоиды равны по величине и противоположны по знаку. Обычно для таких ЭДС и токов под средним значением понимают среднее значение, соответствующее положительной полуволне. В этом случае:
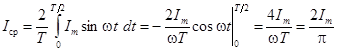 .
.
Аналогично 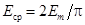 .
.
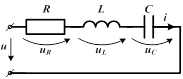
4.2 Установившиеся процессы в простейших цепях с последовательным и соединением элементов
|
В соответствии с законом Кирхгофа в такой схеме приложенное напряжение распределяется между тремя элементами, т.е.
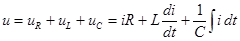 .
.
Задавшись током цепи в виде 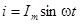 (т.е.
(т.е. 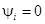 ), для входного напряжения получим
), для входного напряжения получим
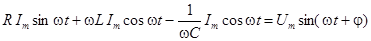 .
.
В данном случае сдвиг фазы совпадает с фазой напряжения 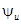 . Найдем амплитуду тока и угол фазного сдвига.
. Найдем амплитуду тока и угол фазного сдвига.
Приведенное выражение справедливо для любых значений t, в том числе для 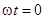 и
и 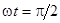 .
.
Использование условия 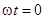 дает равенство
дает равенство 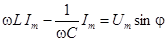
Второе условие 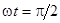 дает:
дает: 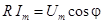 .
.
Возводим каждое из полученных выражений в квадрат и складываем:
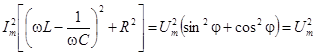 ,
,
откуда 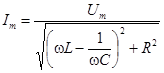 .
.
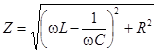 – полное сопротивление последовательной цепи,
– полное сопротивление последовательной цепи, 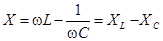 – реактивное сопротивление цепи.
– реактивное сопротивление цепи.
Второе уравнение получим, поделив первое выражение на второе:
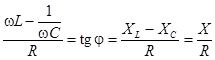 ,
,
откуда угол фазного сдвига 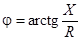 .
.
Следовательно, угол сдвига фаз лежит в пределах: 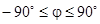 .
.
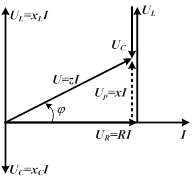
| Можно построить векторную диаграмму для данного случая. Вектор приложенного напряжения равен геометрической сумме трех векторов составляющих напряжения.
Данная диаграмма построена для векторов, равных по величине действующим значениям напряжения и тока.
Направление вектора тока тока выберем произвольно. Вектор активного напряжения 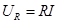 совпадает по фазе с вектором тока. совпадает по фазе с вектором тока.
|
Индуктивное напряжение опережает ток на 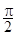 , следовательно, вектор индуктивного напряжения
, следовательно, вектор индуктивного напряжения 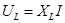 сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение и его вектор
сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение и его вектор 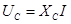 противоположен по фазе вектору
противоположен по фазе вектору 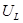 . Замыкающий вектор и есть вектор полного напряжения U .
. Замыкающий вектор и есть вектор полного напряжения U .
При построении этой векторной диаграммы векторы напряжений на участках цепи откладывались в той же последовательности, в какой эти участки включены в цепь. Поэтому отдельным точкам векторной диаграммы (0, a , b , d ) соответствуют одноименные точки цепи. Такая диаграмма может быть названа топографической. Она позволяет сразу найти векторы напряжений между любыми точками цепи, соединив их прямой линией.
В результате сложения векторов получается прямоугольный треугольник напряжений с гипотенузой, равной полному напряжению U, катетом, равным активному напряжению 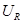 и катетом
и катетом 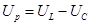 , напряжение которого называется реактивным. На построенной диаграмме преобладает индуктивное напряжение и поэтому реактивное напряжение совпадает по фазе с индуктивным.
, напряжение которого называется реактивным. На построенной диаграмме преобладает индуктивное напряжение и поэтому реактивное напряжение совпадает по фазе с индуктивным.
Следует отметить, что полученные выражения, связывающие амплитудные значения тока и напряжения, могут рассматриваться как аналог закона Ома для переменного тока. Закон Ома в таком виде справедлив только для максимальных и действующих значений переменного тока и напряжения, но не для мгновенных значений, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
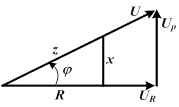
| Если разделить все стороны треугольника напряжений на общий множитель I, получится подобный ему треугольник сопротивлений с гипотенузой Z и катетами R и X, откуда
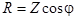 , , 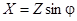 , , 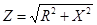 . .
|
4.3 Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости
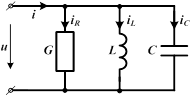
| При параллельном соединении сопротивления R , индуктивности L и емкости С мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников:
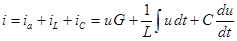 . .
|
Положим 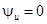 , тогда фаза тока
, тогда фаза тока 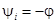 , т.е.
, т.е. 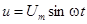 ,
, 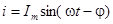 .
.
Подставляя эти выражения в записанное уравнение, получим:
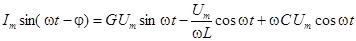 .
.
Это уравнение справедливо для любого момента времени, следовательно мы можем рассмотреть, как и в случае последовательного соединения элементов, два момента 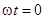 и
и 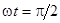 .
.
1) 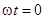 :
: 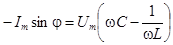 или
или 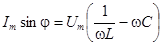
2) 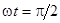 :
: 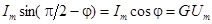 .
.
Далее действуем по аналогии с предыдущим случаем. Возводим в квадрат каждое из этих выражений, складываем и получаем:
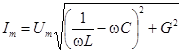 ,
,
где 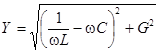 – носит название полной проводимости цепи,
– носит название полной проводимости цепи,
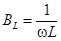 – индуктивная,
– индуктивная, 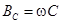 – емкостная,
– емкостная, 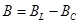 – реактивная проводимость.
– реактивная проводимость.
Угол сдвига фаз 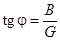 , откуда
, откуда 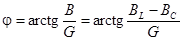 .
.
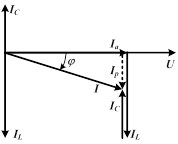
Построим для этого случая векторную диаграмму токов.
|
| Задаемся положением вектора приложенного напряжения U. Активный ток 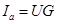 совпадает по фазе с напряжением U, индуктивный ток совпадает по фазе с напряжением U, индуктивный ток 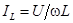 отстает от напряжения на отстает от напряжения на 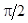 , емкостный ток , емкостный ток 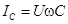 опережает напряжение на опережает напряжение на 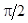 , реактивный ток , реактивный ток 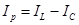 . Тогда действующее значение тока всей цепи . Тогда действующее значение тока всей цепи
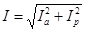 . .
| |
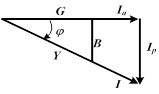
| Полученный треугольник носит название треугольника токов. Если все стороны треугольника поделить на величину напряжения U, то получим подобный треугольник, который носит название треугольника проводимости. | |
Связь между параметрами сопротивлений и проводимостей:
Эту связь легко найти, анализируя треугольники сопротивлений и проводимостей.
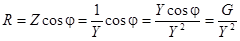 , аналогично
, аналогично 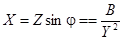 .
.
Проводя подобные преобразования для проводимостей, получим
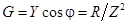 и
и 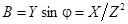 .
.
4.4 Комплексный метод расчета электрических цепей переменного тока
Существенное упрощение достигается изображением синусоидальных функций времени комплексными числами.
Существует несколько форм представления комплексного числа:
- алгебраическая форма: 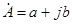 ;
;
- показательная (или экспоненциальная) форма: 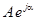 ;
;
- тригонометрическая форма: 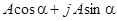 .
.
Все эти формы связаны между собой, в частности, модуль числа 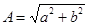 , аргумент
, аргумент 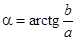 .
.
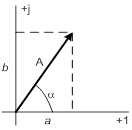
| Для геометрического изображения используется прямоугольная система координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые. Такая плоскость называется плоскостью Гаусса.
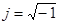 , , 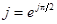 , , 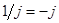
|
Для вещественной и мнимой частей комплексного числа употребляют также обозначения: 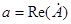 ,
, 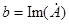 .
.
Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называют сопряженными.
Если 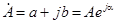 , то сопряженное ему комплексное число запишется в форме
, то сопряженное ему комплексное число запишется в форме 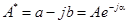 . При этом соблюдается равенство:
. При этом соблюдается равенство: 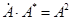 .
.
Пусть имеется синусоидально изменяющийся ток 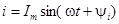 .
.
Его можно представить в форме 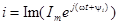 .
.
Комплексное число 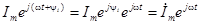 будем рассматривать как символическое изображение действительного синусоидального тока, которое определяется при заданной частоте ω двумя величинами – амплитудой и начальной фазой.
будем рассматривать как символическое изображение действительного синусоидального тока, которое определяется при заданной частоте ω двумя величинами – амплитудой и начальной фазой.
Комплексное число 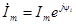 называют комплексной амплитудой тока.
называют комплексной амплитудой тока.
Рассмотрим теперь выражение для производной по времени от синусоидального тока
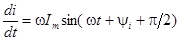
Изображение производной будет иметь вид:
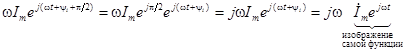
Таким образом, операция дифференцирования действительной функции заменяется умножением на 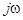 ее комплексного изображения.
ее комплексного изображения.
Рассмотрим изображение интеграла от синусоидальной функции. В частности, заряд сможет быть найден как
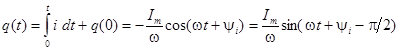 .
.
(Так как мы рассматриваем только случаи, когда приложенное к зажимам цепи напряжение и э. д. с, действующие в цепи, синусоидальны и не содержат постоянных составляющих, то напряжения на конденсаторах и заряды на конденсаторах также не содержат постоянных составляющих).
Искомое изображение интеграла будет
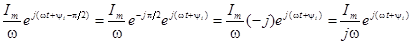
Т. о. операция интегрирования действительной функции заменяется делением на 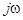 ее комплексного изображения.
ее комплексного изображения.
Таким образом, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.
Алгоритм метода:
1. Замена заданных функций времени их комплексными изображениями.
2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.