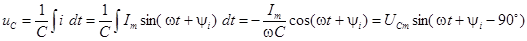Необходимо отметить, что наложение неприменимо для мощностей, так как они являются квадратичными функциями токов и напряжений.
4.3 Принцип взаимности
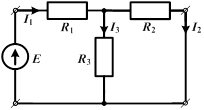
| Пусть в первую ветвь Т-образной схемы, состоящей из трех разных сопротивлений 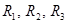 соединенных звездой, включена ЭДС Е, а выходные зажимы замкнуты. Направление токов всех ветвей определяется направлением ЭДС E. соединенных звездой, включена ЭДС Е, а выходные зажимы замкнуты. Направление токов всех ветвей определяется направлением ЭДС E.
|
Ток 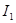 распределится между параллельно соединенными второй и третьей ветвями обратно пропорционально их сопротивлениям. Тогда ток во второй ветви
распределится между параллельно соединенными второй и третьей ветвями обратно пропорционально их сопротивлениям. Тогда ток во второй ветви
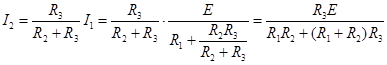 .
.
Если поменять местами индексы 1 и 2, очевидно, получится значение тока 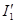 в первой ветви при таком переносе ЭДС Е во вторую ветвь, чтобы ее направление совпало с направлением тока в первой ветви при таком переносе ЭДС Е во вторую ветвь, чтобы ее направление совпало с направлением тока 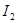 . Выражение . Выражение 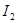 симметрично относительно этих индексов, поэтому симметрично относительно этих индексов, поэтому 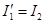 . .
| 
|
Установленный принцип взаимности для Т-образной схемы имеет самый общий характер и может быть сформулирован следующим образом:
если ЭДС Е, действуя в любой ветви сколь угодно сложной цепи, не содержащей других ЭДС, вызывает в другой ветви ток I , то перенесенная в нее та же ЭДС вызовет в первой ветви такой же ток I .
Принцип взаимности был установлен Кирхгофом.
На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одной ЭДС, когда ее перенос упрощает цепь.
4.4 Расчет электрических цепей, основанный на применении уравнений Кирхгофа
Обычно заданными являются величины и направления всех ЭДС источников напряжения и внутренних токов источников тока и значения всех внутренних и внешних сопротивлений или проводимостей цепи, а определяют токи и по ним – напряжения ветвей. Поэтому число неизвестных равно числу р ветвей схемы и, следовательно, столько же независимых уравнений нужно составить по первому и второму законам Кирхгофа,
Так как при составлении уравнений необходимо учесть направления всех токов, то направлениями токов следует задаться. Применяя первый закон, токи, приходящие к узлу и уходящие от него, следует брать с разными знаками. Применяя второй закон, ЭДС и токи, направления которых совпадают с произвольно выбранным направлением обхода контура, следует считать имеющими положительный знак, остальные – отрицательный.
Уравнения, составленные по первому закону Кирхгофа для цепи с q узлами, будут независимыми лишь для 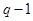 узлов, так как уравнение для последнего узла является следствием предыдущих. Следовательно, по второму закону Кирхгофа надо составить
узлов, так как уравнение для последнего узла является следствием предыдущих. Следовательно, по второму закону Кирхгофа надо составить 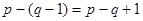 независимых уравнений. Если в цепи присутствуют ветви с источниками тока, количество уравнению по второму закону Кирхгофа
независимых уравнений. Если в цепи присутствуют ветви с источниками тока, количество уравнению по второму закону Кирхгофа 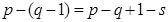 , где s – количество ветвей, содержащих источники тока.
, где s – количество ветвей, содержащих источники тока.
Пример составления системы уравнений.
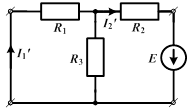
Изображенная на рисунке цепь имеет 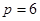 ветвей,
ветвей, 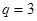 узла и
узла и 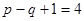 элементарных контура.
элементарных контура.
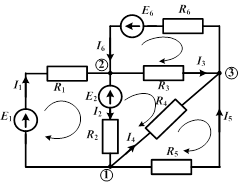
|
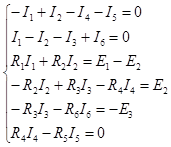
|
Решая систему уравнений любым известным из алгебры способом, находят все неизвестные токи ветвей. Отрицательный знак указывает на то, что действительное направление тока обратно выбранному направлению.
Достоинством рассмотренного метода является его общность, а недостатком – громоздкость решения системы, состоящей из большого числа уравнений. Поэтому кроме непосредственного использования уравнений по законам Кирхгофа применяются специальные методы расчета сложных цепей: либо упрощающие их схемы (методы наложения и эквивалентного источника энергии), либо уменьшающие число неизвестных (методы контурных токов и узловых напряжений).
5. МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
5.1 Метод контурных токов
Метод основан на том, что каждому независимому контуру приписывается некоторый контурный ток, который замыкается по этому контуру.
Обычно в качестве независимых контуров используются элементарные контуры, при этом всем контурным токам придается одно и то же направление, совпадающее с направлением обхода, например по часовой стрелке. Эти контурные токи становятся основными неизвестными задачи, на основе которых определяются реальные токи ветвей.
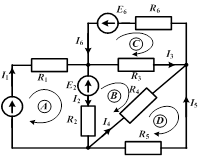
|
Контурные токи, проходящие также по внешним ветвям, являются для этих ветвей реально существующими, например ток 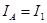 контура А. Контурные токи внутренних контуров, например ток
контура А. Контурные токи внутренних контуров, например ток 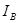 контура В, являются фиктивными величинами, введенными для удобства расчетов. Реальные токи внутренних ветвей можно найти как разность токов двух контуров, в которые входит эта ветвь. Например, для тока
контура В, являются фиктивными величинами, введенными для удобства расчетов. Реальные токи внутренних ветвей можно найти как разность токов двух контуров, в которые входит эта ветвь. Например, для тока 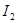 ветви с
ветви с 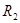 выбранное направление тока совпадает с
выбранное направление тока совпадает с 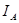 , тогда
, тогда
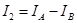 .
.
Взятая по направлению обхода алгебраическая сумма всех ЭДС, входящих в контур, называется контурной ЭДС, сумма всех сопротивлений контура называется контурным сопротивлением. Так, для контуров А и В контурные ЭДС и сопротивления, соответственно, имеют вид:
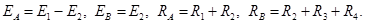
Сопротивление общей ветви двух контуров называется общим сопротивлением, например,
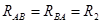 .
.
Тогда вместо уравнения по второму закону Кирхгофа для контура А можно написать:
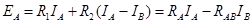 .
.
В это уравнение члены с контурным сопротивлением входят с положительным знаком, члены с общим сопротивлением – с отрицательным.
Если в каком-либо контуре нет источников ЭДС, в правую часть соответствующего уравнения надо подставить нуль. Если два контура не имеют общей ветви, то их общее сопротивление также равно нулю.
Таким образом, вместо системы из р уравнений по первому и второму законам Кирхгофа, по методу контурных токов составляется система из 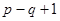 уравнений по второму закону Кирхгофа. Так, для цепи, изображенной на рисунке, вместо шести уравнений (двух по первому и четырех по второму законам Кирхгофа) по методу контурных токов составляется следующая система из четырех уравнений:
уравнений по второму закону Кирхгофа. Так, для цепи, изображенной на рисунке, вместо шести уравнений (двух по первому и четырех по второму законам Кирхгофа) по методу контурных токов составляется следующая система из четырех уравнений:
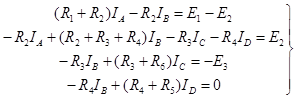
После определения контурных токов находят действительные токи ветвей.
Если в схеме имеются источники тока, то независимый контур следует выбирать таким образом, чтобы каждый источник тока входил только в один контур, тогда контурный ток в этом контуре будет равен току источника.
3.6 Метод узловых потенциалов (напряжений)
Метод основан на применении первого закона Кирхгофа. Составляется 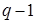 уравнение для потенциалов узлов схемы, при условии, что потенциал одного из узлов принят равным нулю. После того как найдены потенциалы узлов, находят токи в ветвях по закону Ома.
уравнение для потенциалов узлов схемы, при условии, что потенциал одного из узлов принят равным нулю. После того как найдены потенциалы узлов, находят токи в ветвях по закону Ома.
Рассмотрим принцип составления уравнений методом узловых потенциалов на примере конкретной схемы.
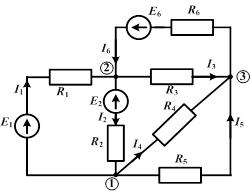
| Здесь 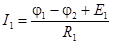 ; ;
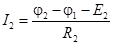 ; ; 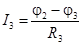 ; ;
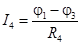 ; ; 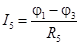 ; ;
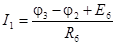 . .
|
Запишем уравнения по первому закону Кирхгофа для узлов 1 и 2 с учетом приведенных выражений для токов:
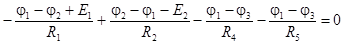 ;
;
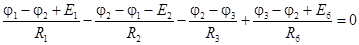 .
.
Далее приведем их к следующему виду:
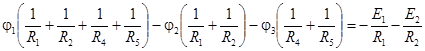 ;
;
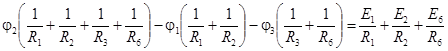 .
.
Пусть потенциал третьего узла равен нулю 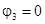 , тогда
, тогда
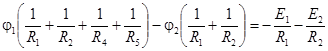 ;
;
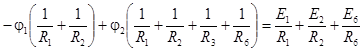 .
.
В результате можно сформулировать следующее правило составления узлового уравнения для потенциалов:
Собственный потенциал узла следует умножить на суммарную проводимость ветвей, образующих этот узел, и вычесть произведения, учитывающие связи между соседними узлами, в которых потенциал соседнего узла умножается на суммарную проводимость ветвей связи.
Правая часть уравнений представляет собой алгебраическую сумму произведений э.д.с. на соответствующие проводимости тех ветвей, которые присоединены к рассматриваемому узлу. Это произведение берется с положительным знаком, когда э.д.с. направлена к узлу.
Если ветвь содержит идеальный источник тока, то он учитывается в правой части уравнения со знаком «плюс», если направлен к узлу.
После решения системы уравнений для потенциалов, токи в ветвях рассчитывают по закону Ома.
3.7 Метод эквивалентного источника
Теоремы компенсации
Теорема Тевенена:
Токи и напряжения в линейной цепи не изменятся, если ветвь заменить источником напряжения, ЭДС которого равна падению напряжения на этой ветви, а направление противоположно направлению заменяемого напряжения.
Теорема Нортона:
Токи и напряжения в линейной цепи не изменятся, если ветвь заменить источником тока, ток которого равен току в этой ветви и совпадает с направлением тока в ветви.
Метод эквивалентного источника
Этот метод применяется для определения тока (или напряжения)
в сопротивлении (проводимости) одной ветви сложной цепи. Если эта
ветвь содержит источники энергии, их следует считать принадлежащими к остальной части сложной цепи.
| Предположим, что нам требуется найти ток в некоторой ветви сложной цепи. Выделим на рисунке эту ветвь, а всю остальную часть цепи условно обозначим прямоугольником А. («А» - активная часть цепи, содержит источники ЭДС) | 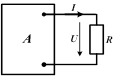
|
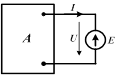
Сопротивление R исследуемой ветви в соответствии с теоремой Тевенена заменяется эквивалентной ЭДС 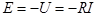 где I и U – искомые ток и напряжение, совпадающие по направлению. где I и U – искомые ток и напряжение, совпадающие по направлению.
| 
|
После этого применяется метод наложения.
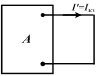
Сначала принимаются в расчет все источники энергии активного двухполюсника, а ЭДС Е замыкается накоротко. Тогда ток 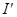 ветви равен, очевидно, току ветви равен, очевидно, току 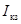 короткого замыкания активного двухполюсника, и совпадает по направлению с током I. короткого замыкания активного двухполюсника, и совпадает по направлению с током I.
| 
|
| Затем учитывается только ЭДС Е. При этом источники энергии, включенные в активный двухполюсник, заменяются их внутренними. В частности, идеальные источники напряжения замыкаются накоротко, а идеальные источники тока – размыкаются. | 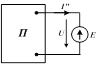
|
Активный двухполюсник превращается в пассивный П. Пусть эквивалентная проводимость этого двухполюсника относительно его зажимов равна GB. Тогда ток ветви для этого этапа, если считать его направление совпадающим с 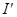 , равен
, равен 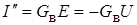 .
.
Действительный ток исследуемой ветви с проводимостью 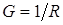 равен алгебраической сумме токов обоих этапов:
равен алгебраической сумме токов обоих этапов:
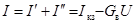 .
.
С другой стороны по закону Ома 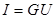 .
.
Откуда 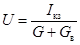 .
.
Если сопоставить эту формулу с выражением для напряжения источника тока, то можно сделать следующий вывод:
активный двухполюсник эквивалентен источнику тока с внутренним током, равным току короткого замыкания двухполюсника, и с внутренней проводимостью, равной проводимости этого же двухполюсника, но без источников энергии.
Из полученного выражения следует, что при холостом ходе, т. е. при 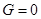 , напряжение на выходных зажимах двухполюсника будет:
, напряжение на выходных зажимах двухполюсника будет:
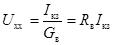
Искомый ток
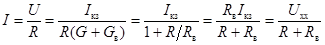
Из аналогии этой формулы с выражением для тока, создаваемого источником напряжения, видно, что
активный двухполюсник эквивалентен источнику напряжения с ЭДС, равной напряжению холостого хода на зажимах разомкнутого двухполюсника и внутренним сопротивлением, равным сопротивлению этого же двухполюсника, но без источников энергии.
Можно предложить следующий алгоритм метода эквивалентного генератора:
1. Изъять ветвь, в которой надо определить ток, заменив ее разностью потенциалов.
2. Любым известным методом, например методом узловых напряжений, определить указанную разность потенциалов (т.е. напряжение холостого хода).
3. Определить входной сопротивление соответствующего пассивного двухполюсника со стороны разомкнутых зажимов.
4. Возвращаясь к исходной схеме записать ток в искомой ветви.
3.8 Потенциальная диаграмма
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Потенциальная диаграмма строится, когда все токи и напряжения в цепи рассчитаны.
3.9 Баланс мощностей
Условие энергетического баланса для любой электрической цепи постоянного тока выражается в виде равенства нулю суммы мощностей по всем элементам:
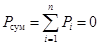 , где п – суммарное число элементов
, где п – суммарное число элементов
схемы.
Уравнение баланса мощностей можно записать в иной форме:
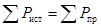 .
.
Это означает, что суммарная мощность, развиваемая источниками электрической энергии, всегда равна суммарной мощности, которая потребляется в цепи. Первая обычно называется генерируемой мощностью, а вторая – потребляемой.
Свойство баланса мощностей, являясь следствием закона сохранения энергии, отражается в уравнениях состояния электрических цепей и относится к общим свойствам электрических цепей.
Потребляемая энергия в цепях постоянного тока связана с выделением на сопротивлениях при протекании тока теплоты и определяется в соответствии с законом Джоуля – Ленца: 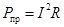
Для идеального источника напряжения генерируемая мощность определяется как 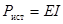 , причем если направление тока совпадает с направлением ЭДС, то произведение берется со знаком «+». Это означает, что источник ЭДС доставляет в цепь энергию.
, причем если направление тока совпадает с направлением ЭДС, то произведение берется со знаком «+». Это означает, что источник ЭДС доставляет в цепь энергию.
Если направление тока встречно направлению ЭДС, то источник не поставляет энергию, а потребляет ее (например, идет заряд аккумулятора). При этом произведение 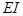 в уравнение энергетического баланса входит со знаком «−».
в уравнение энергетического баланса входит со знаком «−».
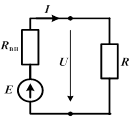
| Если источник неидеальный, то
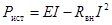
|
Для источника тока
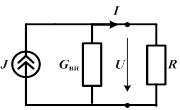
| 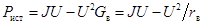 .
Если направление тока источника совпадает с направлением напряжения, то .
Если направление тока источника совпадает с направлением напряжения, то 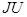 берется со знаком «+», в противном случае – со знаком «−». берется со знаком «+», в противном случае – со знаком «−».
|
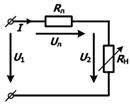
3.9 Линии передачи постоянного тока
Рассмотрим задачу о передаче электрической энергии постоянным током от источника с напряжением 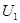 к потребителю. Схема включает в себя постоянное сопротивление обоих проводов линии к потребителю. Схема включает в себя постоянное сопротивление обоих проводов линии 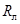 и переменное сопротивление нагрузки и переменное сопротивление нагрузки 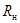 . .
| 
|
Ток в цепи определяется выражением 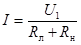 .
.
По мере уменьшения сопротивления нагрузки 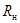 ток будет расти от нуля при холостом ходе ( ток будет расти от нуля при холостом ходе ( 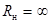 ) до максимального значения ) до максимального значения 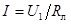 при коротком замыкании ( при коротком замыкании ( 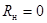 ).
Потери напряжения в проводах линии ).
Потери напряжения в проводах линии 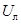 растут линейно с током от нуля (холостой ход) до растут линейно с током от нуля (холостой ход) до 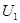 (короткое замыкание): (короткое замыкание): 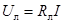 .
Напряжение на приемнике .
Напряжение на приемнике
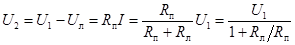 при холостом ходе равно
при холостом ходе равно 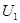 и с уменьшением и с уменьшением 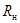 уменьшается до нуля при коротком замыкании. уменьшается до нуля при коротком замыкании.
| 
|
Мощность, отдаваемая источником электрической энергии в цепь, растет прямо пропорционально току:
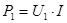 .
.
Мощность, расходуемая в линии передачи, возрастает пропорционально квадрату тока и при коротком замыкании определяет мощность источника:
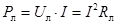
Мощность, потребляемая нагрузкой (полезная мощность),
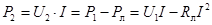
равна нулю и при холостом ходе (так как ток в цепи отсутствует), и при коротком замыкании (в этом случае напряжение на нагрузке 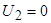 ).
).
Из этого следует, что 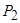 должна иметь максимум. Условие наличия максимума означает равенство нулю первой производной от выражения мощности по току:
должна иметь максимум. Условие наличия максимума означает равенство нулю первой производной от выражения мощности по току:
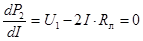
Откуда вытекает, что 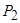 имеет максимум при токе
имеет максимум при токе 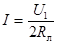 , т.е. при
, т.е. при 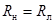
Такой режим работы линии носит название режима согласованной нагрузки.
В этом случае полезная мощность будет максимальна:
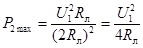
Коэффициент полезного действия 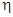 электропередачи равен отношению полезной мощности
электропередачи равен отношению полезной мощности 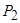 к мощности
к мощности 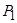 источника:
источника:
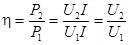 .
.
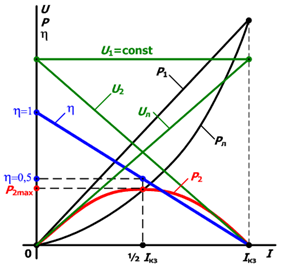
Он равен нулю при коротком замыкании и изменяется по линейному закону, стремясь к единице при холостом ходе. При передаче максимальной мощности КПД равен 0,5, при этом напряжение приемника равно половине напряжения генератора.
Мощность 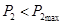 может быть передана в двух режимах, причем в первом режиме КПД и напряжение на приемнике будут больше, а ток меньше, чем во втором. Следовательно, из всех физически возможных режимов работы технически целесообразными будут режимы в левой части графика до
может быть передана в двух режимах, причем в первом режиме КПД и напряжение на приемнике будут больше, а ток меньше, чем во втором. Следовательно, из всех физически возможных режимов работы технически целесообразными будут режимы в левой части графика до 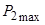 при
при 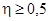 .
.
4. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА В УСТАНОВИВШЕМСЯ РЕЖИМЕ
4.1 Электрические цепи синусоидального тока
Получение синусоидальных напряжений и токов.
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде.
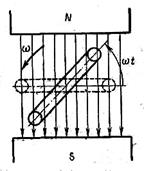
| Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции. При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой. |
Пусть в начальный момент времени 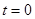 плоскость катушки будет перпендикулярна магнитным линиям. Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол
плоскость катушки будет перпендикулярна магнитным линиям. Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол 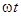 , и мгновенные значения ее потока и потокосцепления будут равны
, и мгновенные значения ее потока и потокосцепления будут равны 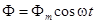 и
и 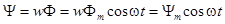 .
.
Тогда мгновенное значение э. д. с. катушки
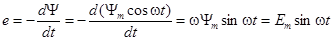 .
.
Временные диаграммы
Синусоидально изменяющуюся во времени величину, например ток, имеющий амплитуду (максимальное значение) 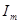 и период повторения Т, можно записать в виде:
и период повторения Т, можно записать в виде: 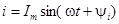
Аргумент синусоидальной функции называют фазовым углом, или фазой:
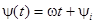 .
.
Угловая частота ω определяет скорость изменения фазового угла: 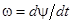 , рад/с. Угловая частота связана с периодом Т и частотой f соотношением
, рад/с. Угловая частота связана с периодом Т и частотой f соотношением 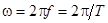 . При фиксированной частоте ω синусоидальную функцию удобно строить в зависимости от переменной
. При фиксированной частоте ω синусоидальную функцию удобно строить в зависимости от переменной 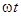 , измеряемой в радианах.
, измеряемой в радианах.
Начальная фаза 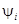 есть значение фазового угла при t = 0.
есть значение фазового угла при t = 0.
На временной диаграмме положительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений 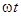 , а отрицательную начальную фазу следует откладывать в сторону положительных значений
, а отрицательную начальную фазу следует откладывать в сторону положительных значений 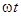 .
.
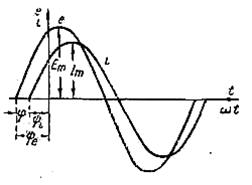
| При совместном рассмотрении двух синусоидальных функций одной частоты разность их фаз, равную разности их начальных фаз, часто называют углом сдвига и обычно обозначают φ. Так, разность фаз ЭДС 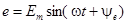 и тока и тока 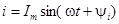 или, иначе, угол сдвига кривой тока относительно кривой ЭДС будет или, иначе, угол сдвига кривой тока относительно кривой ЭДС будет 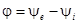 . Если синусоидальные функции одной частоты имеют одинаковые начальные фазы, то говорят, что они совпадают по фазе, а если разность их фаз равна . Если синусоидальные функции одной частоты имеют одинаковые начальные фазы, то говорят, что они совпадают по фазе, а если разность их фаз равна 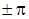 , то говорят, что они противоположны по фазе. , то говорят, что они противоположны по фазе.
|
Векторные диаграммы
Такое изображение можно рассматривать не только как источник дополнительной информации о цепи, но и непосредственно использовать для решения некоторых задач. Рассмотрим, как можно применить вращающийся вектор для изображения синусоидальной ЭДС 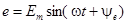 .
.
Возьмем прямоугольную систему осей NOM и условимся откладывать положительные углы против направления часовой стрелки.
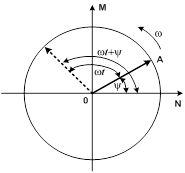
Расположим под углом 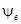 к оси ON вектор ОА, длина которого в выбранном масштабе равна амплитуде ЭДС к оси ON вектор ОА, длина которого в выбранном масштабе равна амплитуде ЭДС 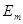 . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол . Будем вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. По истечении промежутка времени t вектор ОА повернется на угол 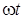 и составит с осью ON угол и составит с осью ON угол 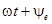 . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: . Тогда величина его проекции на ось OM в принятом масштабе даст значение ЭДС для момента времени t: 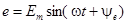 . .
| 
|
Полный цикл изменений ЭДС получится за один полный оборот вектора ОА.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется ее амплитудным значением, а направление – ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма.
Векторные диаграммы особенно удобны при сложении или вычитаний синусоид одинаковой частоты, Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т; е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эта геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью – ее начальную фазу.
Параметры цепей переменного тока
1. Пусть через активное сопротивление протекает синусоидальный ток
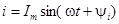 , тогда
, тогда 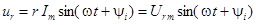
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе. 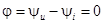 .
.
2. Пусть через индуктивное сопротивление протекает синусоидальный ток
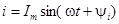 , тогда
, тогда 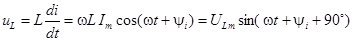
Следовательно, в цепи с индуктивностью L напряжение опережает ток по фазе на 90°. 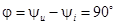 .
.
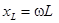 – индуктивное сопротивление (x – обозначает реактивное сопротивление в отличие от активного r).
– индуктивное сопротивление (x – обозначает реактивное сопротивление в отличие от активного r). 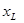 учитывает реакцию самоиндукции (ЭДС самоиндукции, возникающей в катушке при протекании синусоидального тока).
учитывает реакцию самоиндукции (ЭДС самоиндукции, возникающей в катушке при протекании синусоидального тока).
3. Пусть через емкостное сопротивление протекает синусоидальный ток
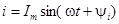 , тогда
, тогда