3 Топологические понятия электрических цепей
3.1 Основные топологические понятия
Содержащаяся в схеме цепи информация о способе соединения элементов дается графом электрической цепи. Для построения графа каждая ветвь заменяется отрезком линии. При этом, если в исходной схеме между какими-то двумя узлами имеется несколько параллельных ветвей, то их следует заменить одной эквивалентной.
Следовательно, граф – это условное графическое изображение схемы, в которой ветви и узлы графа соответствуют ветвям и узлам схемы.
Перед составлением топологических матриц ветви схемы (графа) нумеруют и на них ставят стрелки. Стрелки указывают положительные направления для отсчета тока и напряжения на каждой ветви. Такой граф называется направленным или ориентированным.
При описании графов цепей используют следующие топологические понятия.
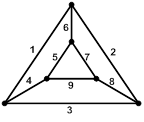
| Путь графа – упорядоченная последовательность ветвей между двумя узлами, в которой каждый узел встречается один раз. Примеры: 9, 4-3-8, 5-7, 5-6-2-8, 4-3-2-6-7 и т.д. Контур – это замкнутый путь, начало и конец которого совпадают. Примеры: 4-1-2-8-9, 5-6-2-3-4 и т.д. |
Если между любой парой узлов графа существует путь, то граф называется связным.
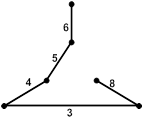
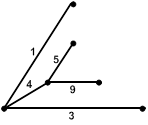
Деревом связного графа называется часть графа, содержащая все узлы и не имеющая ни одного контура.
Дерево связанного графа с q узлами содержит (q −1) ветвь.
| 
| 
|
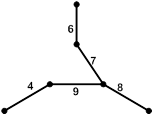
Ветви графа, не вошедшие в выбранное дерево, называются ветвями связи.
Количество ветвей связи: p − (q − 1).
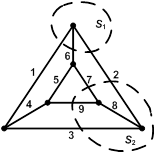
| Сечением графа называется множество ветвей, при удалении которых граф распадается на две части так, одна из которых может быть изолированным узлом.
Сечение на графе или на схеме цепи изображают в виде замкнутой линии, охватывающей часть цепи, включающую один или несколько узлов. 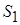 включает ветви 1, 6, 2; включает ветви 1, 6, 2; 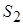 включает ветви 2, 7, 9, 3. включает ветви 2, 7, 9, 3.
|
Число сечений может быть намного больше числа узлов.
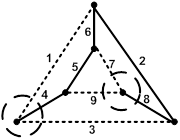
| Главное сечение – это сечение графа, содержащее ветви связи и только одну ветвь выбранного дерева, которая не входит в другие сечения. За положительное направление главного сечения принимается направление ветви дерева данного сечения. |
Главный контур – это контур, состоящий из ветвей дерева и только одной новой ветви связи (количество главных контуров равно количеству ветвей связи). Направление контура определяется направлением ветви связи, образовавшей данный контур.
3.2 Топологические матрицы графов
Для математического описания способа соединения ветвей цепи используются матрицы соединений, контуров и сечений – прямоугольные матрицы, столбцы которых отвечают ветвям цепи, а строки – узлам, контурам и сечениям соответственно. Следовательно, различают узловые матрицы, матрицы сечений и матрицы контуров.
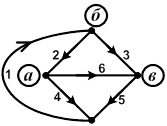
| Рассмотрим граф и составим для него матрицу [А], показывающую, к какому узлу направленного графа присоединены соответствующие ветви. Число строк в такой матрице равно количеству ветвей дерева графа, т.е. числу узлов без единицы. (Если ветвь направлена к узлу, то −1, если из узла +1, если не подходит к узлу, то 0). |
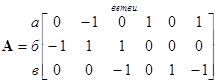
A называется матрицей соединений или узловой матрицей.
Размер матрицы 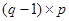 .
.
Система уравнений первого закона Кирхгофа при этом может быть записана в матричной форме:
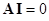 .(I – вектор-столбец токов в ветвях).
.(I – вектор-столбец токов в ветвях).
Матрица сечений Q дает информацию о принадлежности ветвей цепи к определенным сечениям. Если эта матрица составляется для главных сечений, то ее называют матрицей главных сечений. Размер матрицы 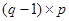 .
.
Если ветвь содержится в сечении и направлена согласно с направлением главного сечения, то соответствующий элемент матрицы имеет значение +1, если направлен иначе, то −1, если ветвь не входит в сечение, то 0.
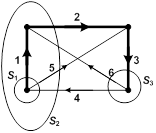
| Рассмотрим пример графа. Выделим одно из деревьев графа. Предположим, что оно образовано ветвями 1-2-3. Для данного дерева можно построить 3 главных сечения:  . Составим матрицу, в которой столбцами являются ветви, а строками - сечения, т.е. . Составим матрицу, в которой столбцами являются ветви, а строками - сечения, т.е.
|
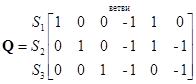 .
.
Матрицу главных сечений можно использовать для записи первого закона Кирхгофа: 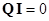 .
.
Матрица контуров В содержит информацию о том, в какие контуры цепи входят ветви. Первоочередной интерес представляют матрицы главных контуров. Напомню, что главными контурами называют контуры, в каждый из которых входит только по одной ветви связи. Направление контура определяется по направлению ветви связи, входящей в него.
В результате строки В-матрицы соответствуют главным контурам цепи, а столбцы – ветвям. Размер матрицы контуров 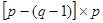 .
.
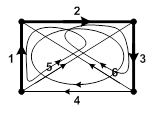
| Для анализируемого дерева графа – 3 главных контура: - образованный ветвями 1-2-3-4; - образованный ветвями 1-2-5; - образованный ветвями 2-3-6. |
В результате матрица принимает вид:
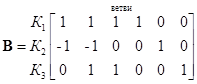 .
.
Второй закон Кирхгофа в матричной форме может быть записан как: 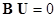 , где U – вектор-столбец, составленный из напряжений ветвей.
, где U – вектор-столбец, составленный из напряжений ветвей.
Между топологическими матрицами существует связь:
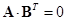 и
и 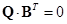 .
.








