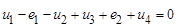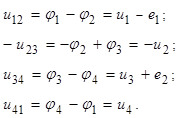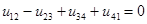2. В рабочем диапазоне ток, генерируемый источником, мало зависит от напряжения на его зажимах.
| Идеализация свойств источников 1-го типа приводит к источнику ЭДС е – элементу, напряжение на зажимах которого не зависит от протекающего через этот источник тока. |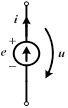 
|
| Идеализация свойств источника 2-го типа – это источник тока, ток которого J не зависит от напряжения и на его зажимах. | 
|
Реальные источники энергии отличаются от идеальных источников тем, что напряжение на их зажимах и ток зависят друг от друга, то есть зависят от нагрузки источника.
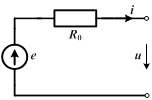
Простейший вариант схемы замещения источника, учитывающий это, включает идеальный источник ЭДС е и его внутреннее сопротивление 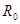 . Внешняя характеристика – зависимость u(i) – такого источника описывается уравнением  .
| 
|
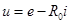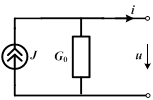
Та же зависимость может быть смоделирована источником тока J и внутренней проводимостью 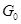 , внешняя характеристика которого выражается соотношением  .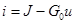
| 
|
Это преобразование является эквивалентным, т.к. не изменяет тока и напряжения в других частях схемы.
Сопоставление обеих внешних характеристик показывает, что обе схемы эквивалентны друг другу при выполнении условий
; 
.
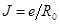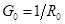Эти соотношения позволяют осуществить замену идеального источника ЭДС е и сопротивления 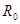эквивалентным параллельным соединением идеального источника тока и того же сопротивления.
Идеальные источники ЭДС, обладающие нулевым внутренним сопротивлением, и источники тока с нулевой внутренней проводимостью (или бесконечным внутренним сопротивлением) не могут быть эквивалентно преобразованы друг в друга.
Для описания свойств компонентов электронных цепей вводят управляемые источники ЭДС и тока. В таких источниках их ЭДС и токи зависят от напряжений или токов на других участках рассматриваемой электрической цепи.
Существует четыре типа управляемых источников:
1. Источник напряжения, управляемый напряжением (ИНУН) .
2. Источник тока, управляемый напряжением (ИТУН).
3. Источник напряжения, управляемый током (ИНУТ).
4. Источник тока, управляемый током (ИТУТ).
2. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
2.1 Основные задачи теории электрических цепей
При исследовании электрических цепей выделяют две основные задачи – анализа и синтеза.
Задача анализа – заданы воздействия, структура цепи и параметры элементов; требуется определить реакцию цепи.
Задача синтеза – заданы воздействия и реакции цепи; требуется определить структуру и параметры элементов цепи.
Напряжения источников ЭДС и токи источников тока называются воздействиями. Все остальные токи и напряжения называются реакциями цепи.
Свойства линейных электрических цепей
Линейные электрические цепи – цепи, состоящие только из линейных элементов. Линейные элементы те, параметры которых не зависят от величины токов и напряжений (от величины электромагнитного поля).
Линейные электрические цепи удовлетворяют принципу суперпозиции (наложения), согласно которому реакция цепи на совокупность воздействий равна сумме реакций, вызываемых в этой цепи каждым воздействием в отдельности.
Графическое изображение электрической цепи называется электрической схемой.
|
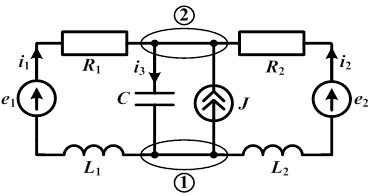
В общем случае электрическая цепь и, следовательно, схема, состоит из ветвей и узлов.
Ветвь – это участок электрической цепи (схемы), вдоль которого протекает один и тот же ток. Элементы ветви соединены последовательно, а общее напряжение равно алгебраической сумме напряжений на каждом элементе. Направление напряжения учитывается знаком слагаемого.
Параллельное соединение нескольких ветвей означает, что они подсоединены к одной и той же паре узлов, и к ним приложено одно и то же напряжение.
На рисунке приведена электрическая цепь, четыре ветви которой соединены параллельно.
Узел (вершина) – место соединения трех и более ветвей электрической схемы.
Основные законы электрических цепей
Для расчета электрических цепей необходимо учитывать направление токов и напряжений. Хотя в общем случае ток является движением электрических зарядов разных знаков в противоположные стороны, условным положительным направлением тока принято считать направление перемещения положительных зарядов, т. е. от положительного зажима источника к отрицательному “-“.Если ток идет в противоположном направлении, он получает отрицательный знак.
В соответствии с законом Ома положительное направление напряжения совпадает с положительным направлением тока. Если направление тока неизвестно, его приходится выбирать произвольно и определять направление в результате расчета по знаку тока (напряжения).
Основные уравнения цепей вытекают из уравнений Максвелла, в частности из принципа непрерывности электрического тока и закона электромагнитной индукции.
Из принципа непрерывности получаем первый закон Кирхгофа:
,
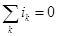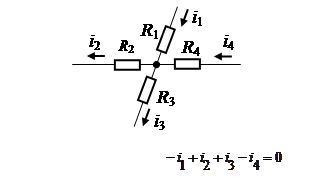
алгебраическая сумма токов в ветвях, образующих узел, равна
нулю. При этом токи, уходящие от узла считают положительными,
а токи, приходящие к узлу – отрицательными.
|
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру электрической цепи, поскольку и в данном случае накопление заряда отсутствует. Контуром называется замкнутый путь, проходящий по нескольким ветвям. В зависимости от числа контуров. Если к узлу присоединен источник тока, то ток этого источника также необходимо учитывать.
Из закона электромагнитной индукции получаем второй закон Кирхгофа в следующем виде
,
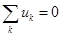т. е. алгебраическая сумма напряжений на ветвях, образующих контур, равна нулю. При этом со знаком «плюс» учитываются величины, совпадающие по направлению с направлением обхода контура. При этом помним, что напряжения совпадают по направлению с током. Если в ветвях контура включены источники напряжения, то формулировку можно изменить: алгебраическая сумма падений напряжения на пассивных элементах цепи равна алгебраической сумме ЭДС источников, действующих в этом контуре.
.
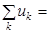
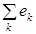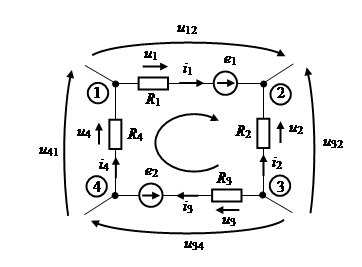
Обход контура осуществляют в произвольно выбранном направлении, (например по часовой стрелке) с соблюдением следующего правила: все контурные ЭДС и падения напряжения, совпадающие с выбранным обходом, записываются с одинаковыми знаками.
|
|
Закон Джоуля-Ленца. Мгновенная мощность p, [Вт], рассеянная в сопротивлении R при протекании электрического тока i, равна:
.
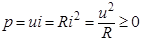Энергия, [Вт∙с], потребляемая сопротивлением, начиная от момента времени равного нулю и до некоторого момента времени t, будет равна:
.
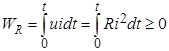