Используют вывод: к единицам прибавляем единицы, к десяткам десятки. По программе Н.Б.Истоминой сначала в 1 классе изучают все случаи без перехода через десяток.

На этой странице рассматривается случай сложения двузначного числа и разрядного без перехода через разряд.
М1И, ч.2, стр. 50

На этой странице рассматривается случай вычитания из двузначного неразрядного числа разрядного без перехода через разряд.
М2И, ч.1, стр. 21

На этой странице рассматривается частный случай прибавления к двузначным однозначных, когда в сумме получается круглое число.
М2И, ч.1, стр. 24
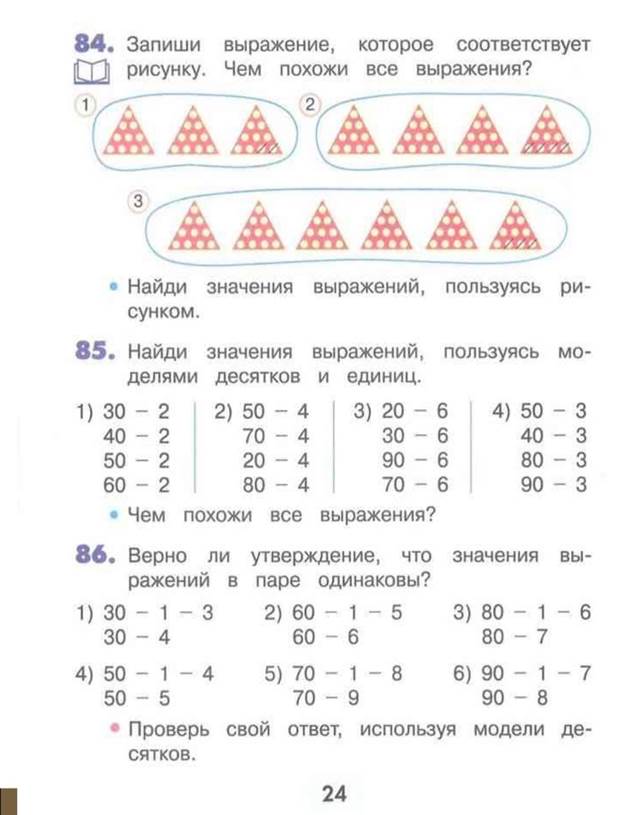
На этой странице рассматривается случай вычитания однозначного числа из круглого.
М2И, ч.1, стр.94
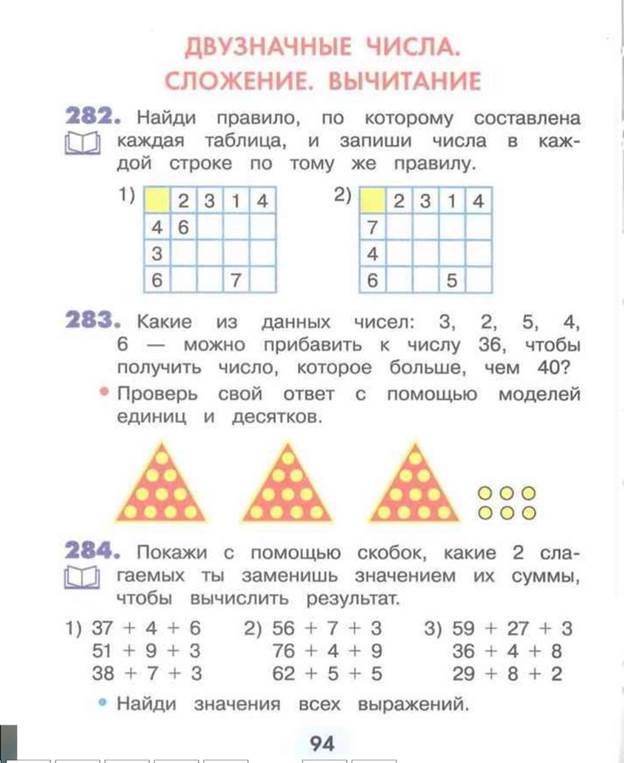
На этой странице рассматривается случай сложения двузначных и однозначных чисел с переходом через десяток.
М2И, ч.1. стр. 108
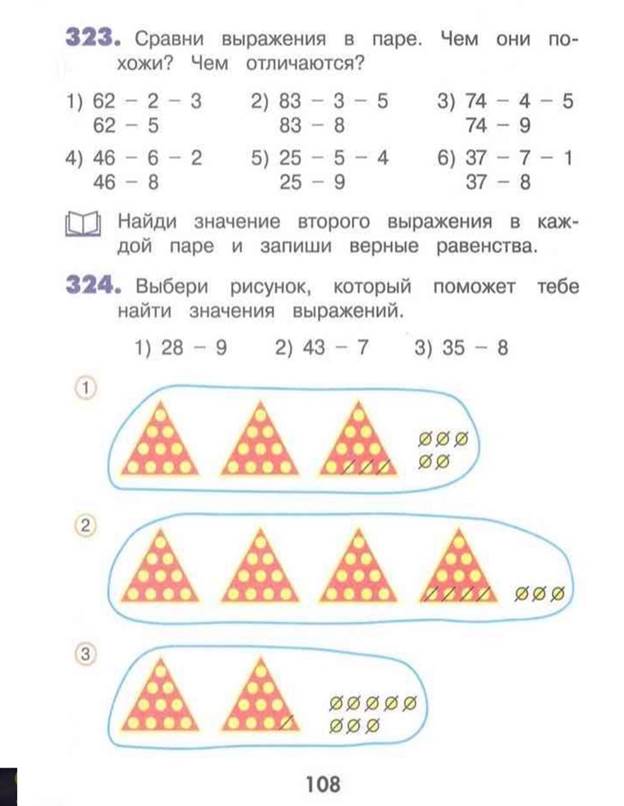
На этой странице рассматривается случай вычитания из двузначного числа однозначного с переходом через разряд.
6. Опишите методический подход к изучению темы «Сложение и вычитание двузначных чисел», который положен в основу учебника М 2 И. И. Аргинской.
Главная задача учителя состоит в том, чтобы формировать у младших школьников прочные навыки сложения и вычитания двузначных чисел.
Формирование вычислительных навыков должно осуществляться на основе сознательного использования приемов вычислений.
При этом учитель может использовать некоторые приемы, помогающие формированию вычислительных навыков:
– комплексные подготовительные упражнения;
– использование опорных сигналов;
– включение в «устный счет» примеров из жизни;
– игровые ситуации, игры;
– задание на развитие самоконтроля.
Для решения поставленных задач использовались следующие методы исследования:
-изучение литературы по данной теме;
-наблюдение;
-беседа, опрос, анализ результатов работ учащихся;
-экспериментальная работа с учащимися. (ред.)
К началу изучения темы «Сложение и вычитание в пределах 100» младшие школьники знают смысл действий сложения и вычитания, коммутативный закон сложения (перестановка слагаемых), связь чисел при сложении и вычитании, умеют прибавлять и вычитать по частям в пределах 10 и 20, умеют выполнять действия сложения и вычитания в случаях, основаных на знании десятичного состава чисел, знакомы с порядком действий в выражениях со скобками, а также в выражениях содержащих несколько действий сложения и вычитания.
Рассмотрим сложение в случаях вида 36 + 2, 36 + 20. Правило сложения двузначных чисел.
Прежде чем перейти к усвоению нового приема устных вычислений, необходимо повторить:
– знание десятичного состава двузначных чисел (28 – это 2 дес. и 8 ед.);
– умение разложить двузначное число на десятки единицы (36 = 30 + 6).
В этом случае можно предложить детям игру «Закрой форточку». Например: 57 = 50 + •.
В качестве подготовительных упражнений используются задания вида:
26 84 42 58
20 6 80 4 40 2 50 8
Прием вычитания в случаях вида 60 – 24. Целесообразно в качестве подготовки больше уделять внимания решению примеров на сложение с ответом 10 и на вычитание из 10, повторить таблицы сложения и вычитания в пределах 10.

7. Составьте самостоятельную работу по теме «Сложение и вычитание в пределах 100», цель которой выяснить, сформирован ли у учащихся вычислительный навык.
Самостоятельная работа.
Фамилия, имя ______________________________________________ .
1. Продолжи ряды чисел (5 чисел).
693, 683, 673, 663, ______________________________________________
305, 308, 311, 314, ______________________________________________
2. Запиши выражения и вычисли их значения.
Разность чисел 48 и 12 _______________________________________
Число 74 увеличить на 7 ________________________________________
Сумма чисел 26 и 13 ________________________________________
Число 98 уменьшить на 6 _____________________________________
На сколько число 52 больше числа 27 __________________________
3. Найди значения выражений.
56 + 35 = 74 - 50 = 53 + 32 = 86 - 34 =
45 – 27 = 27 + 40 = 64 + 12 = 87 - 65 =
4. >, < или =.
49+ 13 … 48+ 5 75 – 30 … 51 - 4
83 – 40 … 25 + 7 56 + 8 … 70 - 13
5. Реши задачу. «До обеда школьники посадили 27 деревьев, а после обеда на 3 дерева больше. Сколько всего деревьев посадили  школьники за день?
школьники за день?
8. Какие приемы самоконтроля может использовать учитель при формировании устных приемов сложения и вычитания в пределах 100? Покажите возможность использования нескольких различных приемов самоконтроля в конкретных условиях.
Для того, чтобы выполнять сложение и вычитание чисел в пределах 100, причем выполнять эти операции устно, в начальной школе изучаются различные приемы.
Приемов, которые изучаются для устного сложения и вычитания в концентре 100, существует достаточно много. Их изучение последовательно. Причем рекомендуется изучать сначала более легкие, потом более сложные. Уровень сложности изучаемых приемов зависит от следующих фактов:
v количество операций, входящих в изучаемый прием;
v на сколько уверенно владеют ученики теми или иными операциями, входящими в данный прием;
v от сходства или различия операций, входящих в данный прием;
v от способа моделирования приемов.
1. Способ: Сложение круглых десятков
40+20
10+70
50+30
Вычислительные приемы:
4 дес. + 2 дес. = 6 дес.= 60
1 дес. + 7 дес. = 8 дес. = 80
5 дес. + 3 дес. = 8 дес. = 80
Знания, умения, навыки необходимые для овладения приемом:
1) Разрядный состав числа.
2) Табличное сложение в пределах 10.
2. Способ: Прибавление к двухзначному числу круглых десятков и прибавление однозначного числа без перехода через десяток.
34+20
34+2
Вычислительные приемы:
(30+4)+20 – разрядные слагаемые, представление в десятичной системе счисления.
34+20=(30+4)+20=(30+20)+4=50+4=54
34+2=(30+4)+2=30+(4+2)=30+6=36
Знания, умения, навыки необходимые для овладения приемом:
1) Разрядный состав числа.
2) Табличное сложение в пределах 10.
3) Правила прибавления числа к сумме:
v переместительное свойство сложения;
v сочетательное свойство сложения.
3. Способ: Прибавление к двузначному числу однозначное с получением круглых десятков.
26+4
32+8
45+5
Вычислительные приемы:
26+4=(20+6)+4=20+(6+4)=20+10=30
Знания, умения, навыки необходимые для овладения приемом:
1) Разрядный состав числа.
2) Правило прибавление числа к сумме.
3) Табличное сложение.
Использование приёмов самоконтроля
Для каждого из вас я приготовила индивидуальную карточку, где записано одно из этих числовых выражений. Выполните задание и объясните, как вы его выполняли.
(36+2 36+20 38-2 56-20)
Посмотрите на условные обозначения рядом с упражнением (+, -)
Я предлагаю вам поработать в парах, а для удобства выполнения этого задания я приготовила вам карточки, на которых вы будете работать.
(15 О 9 О 7=13 42 О 6 О 6=30
20 О 3 О 6=17 37 О 8 О 5=40
54 О 5 О 4=45 28 О 7 О 6=29)
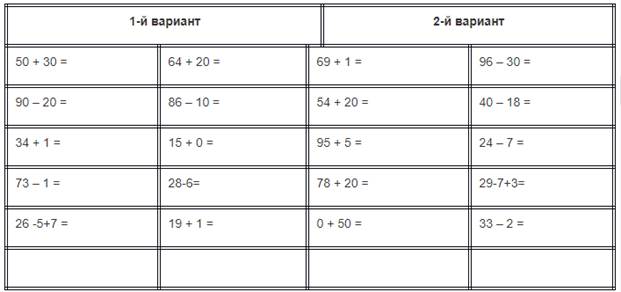
9. Объясните причины следующих ошибок, которые допускают ученики:
а) 50-36=26 б)54+2=76 в) 37+28=64 г) 76-20=50
56-30=14 57- 40=53 58+6=63 64+30=90
Какую работу по предупреждению и исправлению этих ошибок следует проводить?
А) 50-36=26; 56-30=14
Смешение приемов вычитания, основанных на свойствах вычитания суммы из числа и числа из суммы.
Б) 54+2=76; 57-40=53
Выполнение сложения и вычитания над числами разных разрядов как над числами одного разряда.
В) 37+28=64; 58+6=63
Ошибки в табличных случаях сложения и вычитания, когда они входят в качестве операций в более сложные примеры на сложение и вычитание.
Г) 76-20=50; 64+30=90
Получение неверного результата вследствие пропуска операций, входящих в прием, или выполнения лишних операций.
Работа над данными ошибками.
А) Чтобы не допустить появление подобных ошибок, надо проводить специальную работу по сравнению смешиваемых приемов, выявляя при этом существенное различие. Ученикам предлагаются пары примеров, аналогичные приведенным, решая которые, они сравнивают каждый следующий шаг.
Б) Чтобы не допустить данных ошибок полезно обсудить неверные решения примеров. Сначала предлагается найти среди данных примеров те, при решении которых допущена ошибка. Затем выясняется, какая допущена ошибка. После этого еще раз повторяется, что единицы прибавляют к единицам, а десятки к десяткам.
В) Не совершению этих ошибок будет служить постоянное внимание к усвоению учениками табличных случаев сложения и вычитания, особенно случаям с переходом через десяток. Для устранения ошибок необходима индивидуальная работа с учениками, допускающими их.
Г) Эти ошибки, как правило, возникают в результате не внимательности учеников. Для их устранения необходимо научить и постоянно побуждать учеников выполнять проверку решения примеров. В данном случае будет использоваться проверка, основанная на связи между компонентами и результатом действий сложения и вычитания.
10. Какова теоретическая основа приемов устного сложения и вычитания трехзначных чисел? Назовите эти приемы. Найдите в различных учебниках математики страницы, связанные с изучением этих приемов. Приведите примеры рассуждений учащихся при выполнении сложения и вычитания в пределах 1000.
Письменные приемы сложения и вычитания раскрываются вслед за устными приемами. Сначала изучают письменные приемы сложения, а затем вычитания.
При сложении столбиком используется правило сложения суммы с суммой. Это правило повторяют перед тем, как ознакомит детей с письменным приемом сложения. Для этого решают примеры: (8+7)+(2+3) Учащиеся вспоминают как можно по-разному вычислить результат. Затем правило применяется к сложению сумм нескольких слагаемых с числами сразу в пределах 100, затем в пределах 1000,например:
(300+40+5)+(200+20+4)=(300+200)+(40+20)+(5+4)=569
Решив несколько таких примеров, дети замечают, что удобнее складывать сотни с сотнями, десятки с десятками, единицы с единицами. При этом полезно установить какие числа складывали (345 и 224).
Такой подготовительной работы вполне достаточно, чтобы ввести общеизвестную запись письменного приема сложения столбиком.
Письменное сложение изучается в таком порядке:
v Случаи, где сумма единиц и сумма десятков меньше 10
v Случаи, где сумма единиц или сумма десятков равна 10
v Случаи, где сумма десятков или сумма единиц больше 10
Прежде всего решаются примеры на сложения без перехода через десяток:232+347, 235+43. Учащиеся сначала решают их устно с подробной записью в строчку приема вычисления, затем учитель показывает запись этих примеров в столбик, поясняя: числа записывают так, чтобы единицы второго числа были под единицами первого, десятки под десятками, сотни под сотнями.








