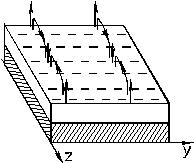
Диэлектрическая замедляющая система.

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1 - вакуум.

2 - немагнитный диэлектрик.

Сделаем предположения:

1. Длина волны в волноводе λ_В ˂ λ₀ , h ˂ β₀..

2. Система бесконечно протяженна вдоль *y и z.

3. Исследуется гармоническая волна, распространяющаяся вдоль z.

Вектор Н - имеет одну составляющую неизменную вдоль y: 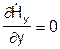, силовые линии - бесконечные нити параллельные оси y.

Исследуем поле в вакууме: 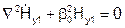, решение ищем в виде: ,

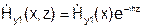тогда: 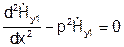, , 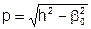где р - аналог поперечного волнового числа в полых волноводах.

Общее решение: .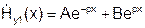

Поле не может бесконечно возрастать, т.е. В=0 и .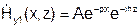

Замедленная волна является поверхностной, амплитуда убывает по экспоненте при удалении от границы раздела.

Чем меньше υ_ф (меньше λ_в), тем больше р и поле сильнее «прижимается» к направляющей системе.

Составляющие Е найдем из первого уравнения Максвелла: .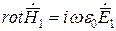

Вычисляем ротор в декартовой системе координат:

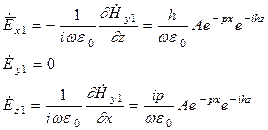
Полученная волна – Е – типа, у которой Пz - чисто действительная, Пx - мнимая.

Поле во 2-й среде 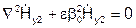, решение в виде: 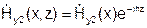, причем h - одно и то же в 1-й и 2-й среде (единый волновой процесс).

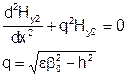
Общее решение: .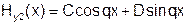

С и D следует выбирать граничных условий при x = a, x = 0.

На поверхности идеального проводника: 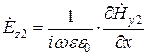должна обращаться в ноль, то есть: D=0 и .

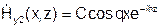Остальные составляющие:

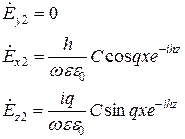
Используем граничные условия на границе раздела вакуум - диэлектрик при х=а .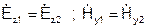

Подставляем выражения:

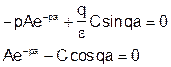
Чтобы система имела отличные от нуля решения, ее определитель должен обращаться в ноль, т.е.:

,

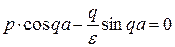или в безразмерном виде: 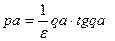(3.25)

Уравнение (3.25) - дисперсионное уравнение замедляющей системы.

Чтобы определить q и p следует использовать: 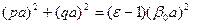(3.26)

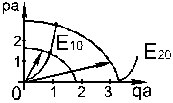Уравнение (3.26) описывает окружности радиуса: .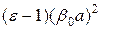

Пересечение кривых - решение; первый индекс - номер корня, второй - поле однородно по y.

Е₁₀ - низший тип волны существующей при любой частоте и толщине слоя диэлектрика:

.

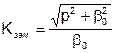Одноволновой режим вплоть до R = π значения (для волн Е-типа), т.е.: .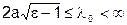

Структура для Е₁₀:

Отношение касательных к границе раздела - составляющих Е и Н называют поверхностным сопротивлением:

.

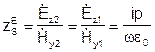Величина Z_с^Е - чисто мнимая (реактивное, индуктивное по характеру сопротивление), т.е. отсутствует средний за период поток энергии вдоль оси х.

Вывод для вол Н-типа аналогичен и для них 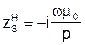, и для самой низшей волны 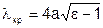, т.е. реальный одномодовый диапазон для всех типов волн .

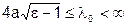Следует отметить, что в качестве линий замедленных волн можно использовать любые системы с реактивным поверхностным сопротивлением.

Существует много способов создания реактивного поверхностного сопротивления, например:

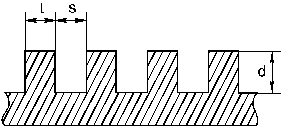Каждая канавка подобна отрезку линии длиной d.

Если d ≤ λ /4, то сопротивление чисто мнимое и имеет характер L. Если (S+t) ˂˂ λ, то можно пренебречь влиянием тонких перегородок и полагать, что вблизи поверхности имеется плоскость с реактивным сопротивлением.

Структура почти такая же, как у диэлектрика с металлом и υ_ф ˂ υ_ф0.

Такие замедляющие системы обычно используют как элемент антенных систем:

.

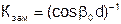Свернутая в трубочку - антенна на луноходе, обратная - диафрагмированный волновод.

Линия Губо

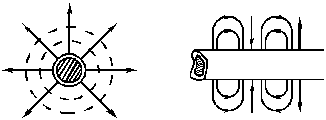Линия Губо представляет собой цилиндрический проводник радиуса R, покрытый

тонким слоем диэлектрика.

Структуру волны легче всего представить, если свернуть в трубку металлическую пластину, покрытую слоем диэлектрика.

Чем толще слой диэлектрика и тоньше проводник, тем больше потери на СВЧ диапазоне, диэлектрик порядка 0.05...0.1мм, проводник диаметром не меньше 1мм.

Затухание в такой линии с полистироловым покрытием в 2-3 раза меньше, чем в прямоугольном волноводе.

Роль диэлектрика может выполнять окисел (или даже скин-слой).

Главный недостаток - линия открытого типа. Если, кроме того, есть изгибы линии, потери резко возрастут.

Возбуждают обычно с помощью рупора:

Диэлектрические волноводы

Диэлектрические волноводы это одно из наиболее перспективных направлений развития линий передачи электромагнитных сигналов в настоящее время (в основном в виде волоконного световода).

Рассмотрим бесконечно длинный диэлектрический цилиндр радиуса а, выполненный из диэлектрика с параметрами (1); расположенный в среде с параметрами (2).

,

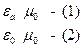Задачу удобнее решать в цилиндрической системе координат.

Для продольных составляющих:

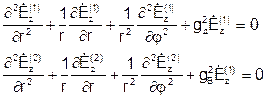
где

.

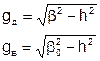Общее решение первого уравнения - линейная комбинация функций Бесселя и Неймана, однако, напряженность в любой точке внутри диэлектрического цилиндра (в том числе и в точке где r=0) должна быть конечной и следовательно:

.

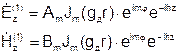Вне цилиндра, где структура должна соответствовать структуре поверхностной волны, амплитуды полей должны убывать по экспоненте при удалении от границы раздела.

Этому требованию удовлетворяют функции Ханкеля второго рода от чисто мнимого аргумента:

.

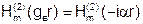Поэтому:

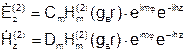
Используем уравнение перехода от продольных к поперечным составляющим и получаем:

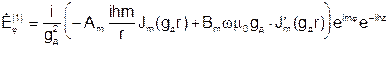
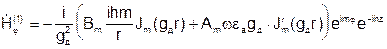
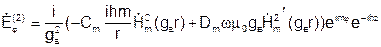
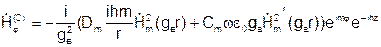
Продольное число h одинаково и в первой и во второй среде.

На границе раздела двух диэлектриков r = a, тангенсальные составляющие ЭМП должны быть непрерывны:

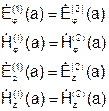
Подставляем в граничные условия выражения для составляющих Е и Н и исключаем коэффициенты Am, Bm, Cm, Dm. Получаем трансцендентное уравнение:

.

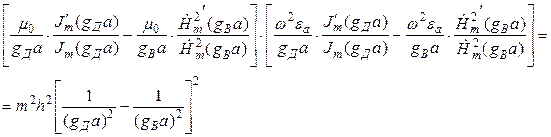Это уравнение служит для определения неизвестного коэффициента h (численно или графически).

Детальный анализ позволяет заключить следующее:

1. В диэлектрическом волноводе может существовать бесконечно большое число различных типов волн, имеющих различный характер изменения поля по координатам r, .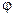

2. В диэлектрическом волноводе невозможно раздельное существование несимметричных волн Е и Н.

Оба этих типа образуют единую смешанную волну и распространяются совместно.

Симметричные волны 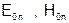могут существовать в диэлектрическом волноводе независимо друг от друга.

3. Каждый тип волны имеет свою критическую частоту, которая находится из условия:

.

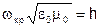Низшим типом волны является волна НЕ₁₁. Эта волна не имеет критической частоты, т.е. может распространяться вдоль диэлектрического стержня на всех частотах и при любом диаметре стержня.

Н₁₁ Е₁₁

4. Величина фазовой скорости волны в диэлектрическом волноводе лежит между величиной фазовой скорости волны Т-типа, распространяющейся в среде окружающей волновод, и величиной V_Ф этой волны в среде с параметрами ε_а , μ₀..

5. Энергия волны распространяется внутри и вне диэлектрического стержня. Чем больше радиус стержня по сравнению с длиной волны ЭМ колебания и чем больше соотношение ε_а / ε₀ , тем большая часть энергии распространяется внутри диэлектрического стержня. При приближении ω к ω_кр , энергия внутри стержня стремится к нулю.

У волны НЕ₁₁ энергия внутри стержня стремится к нулю при a / λ→0.

Для возбуждения волн в диэлектрическом стержне можно использовать схему:

Скосы служат для уменьшения отражения.

На практике диэлектрические волноводы используется в УКВ диапазоне в качестве элементов конструкции антенн и в более коротковолновом диапазоне как линии передачи.

Линии передачи (световоды) представляют собой тонкую (несколько микрометров) нить из особо чистого кварца или искусственного полимера.

Погонные потери в такой линии не превышают нескольких дБ/км (по данным опубликованных в информационных сборниках получены волокна, у которых затухание ∆_вол ˂ 0,1дБ/км.)

Для сравнения, в прямоугольном на 10 ГГц затухания примерно 0.02 дБ/м.

Несущая частота в оптическом диапазоне очень высока и полоса пропускания очень широкая - скорость передачи информации до тысяч Мбит/с.

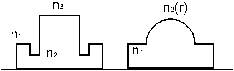На практике используют световоды с различной геометрией поперечного сечения и различными профилями показателя преломления (1-ступенчатый, 2-градиентный, реальные профили изрезаны (чисто технологически)).

Наиболее оптимальный закон для градиентного - параболический:

,

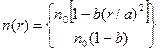первая формула при r ˂ а, вторая при r ≥ а.

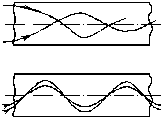При таком законе все меридиональные лучи лежат в плоскостях содержащих ось z, входящие в волокно в одной точке под разными углами, пересекают ось волноводе в одной и той же точке, то же самое относительно параллельно входящих лучах в разных точках (смотри рисунок):

Т.е. различные моды имеют одинаковое время распространения - отсутствует межмодовая дисперсия. Моды - сигналы входящие под разными углами.

На самом деле есть не только меридиональные лучи, но и косые (винтовые) и т.д. - для них дисперсия есть.