Диаграмма волн в круглом волноводе
Волновод работает в одномодовом режиме (Н11) при 2,61а ≤ λ0≤ 3,41а, т.е. коэффициент широкополосности (перекрытия) - 1,3, а реально еще меньше.
Хотя технологически и конструктивно круглый волновод предпочтительней прямоугольного, он используется в основном в виде коротких отрезков. Причина - явление поляризационной неустойчивости. Зато наличие симметричных типов (m=0) практически весьма ценно для создания вращающихся сочленений.
В круглом волноводе обычно используют волны типов Е01,Н01.
Картина для Н01:
 |
Еще одна интересная конструктивная особенность круглого волновода - возможность передачи мощности почти вдвое превосходящую аналогичную для прямоугольного.
Для в волны Н11 (для любой, когда m≥0) величина предельно допустимой мощности не намного превосходит допустимую мощность для прямоугольного (отсутствие граней), а поляризация – линейная:
.
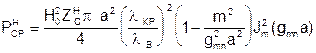Если возбудить две волны Н11, ортогональные друг другу и сдвинутые по фазе на 90 градусов, то получим волну с круговой поляризацией с допустимой напряженностью поля в каждой точке, но с удвоенной мощностью.
Интересные свойства наблюдаются у волны Н0 типа в круглом волноводе. Т.к. поверхностный ток для нее имеет только азимутальную составляющую, то с ростом частоты потери стремятся к нулю.
Коаксиальный волновод
Общее для волн Т-типа Еz = Нz =0. Такое возможно, если волна распространяется вдоль направляющей системы без отражений, то есть для любой составляющей решение имеет вид:
.
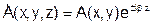Коэффициент фазы и продольное волновое число при этом совпадают:
.
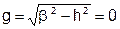Для волн Т-типа (всегда имеется в виду низший тип волны):
,
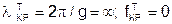т.е. волновод должен пропускать колебания любых частот вплоть до постоянного тока.
В волноводе с волной Т-типа должны быть минимум два проводника разделенных слоем диэлектрика.
Волновой фронт перемещается со скоростью: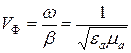 
.
Волны Т-типа не имеют дисперсии.
 |
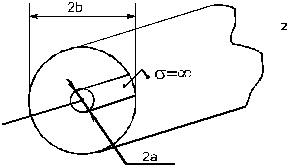Коаксиальный волновод - это два соосных цилиндра.
В однородной материальной среде без зарядов третье уравнение Максвелла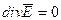 
будет всегда выполняться, если принять: 
;
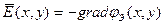φЭ - вспомогательная функция - скалярный электрический потенциал.
Знак «-» выбран, чтобы вектор Е начинался на «+» и заканчивался на «-» зарядах (принято в электротехнике).
Подставляем: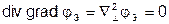 
.
Для коаксиальной линии (в дальнейшем КЛ) удобнее использовать ЦСК.
Из-за полной симметрии волновода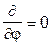 
двумерное уравнение Лапласа принимает вид:
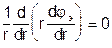или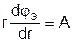 
.
Общее решение этого уравнения: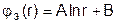 
.
Постоянные А и В следует определять из граничных условий.
Полагаем потенциал наружного проводника равным нулю (заземлён), а внутреннего равным U тогда:
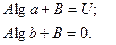
Определяем А и В и получим:
.
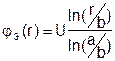Амплитуду вектора Е определим как:
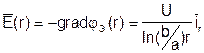, (3.20)
то есть Е имеет только r-ю составляющую и для комплексной амплитуды (диэлектрик без потерь):
.
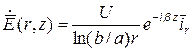Для определения Н используем второе уравнение Максвелла:
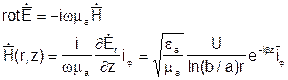
т.е. Н имеет только азимутальную составляющую, а отношение Е к Н в каждой точке пространства равно характеристическому сопротивлению среды, заполняющей коаксиальную линию:
.
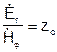Токи на металле имеют только Z составляющую и разное направление на внутренней и внешней трубе, причем их амплитуды равны:
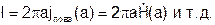
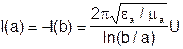
Для коаксиальной линии в отличие от полых волноводов удобно ввести волновое сопротивление:
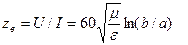(3.21)
( 
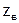не связано с потерями энергии - это только коэффициент пропорциональности).
Зная Е и Н определим мощность переносимую вдоль оси волновода:
.
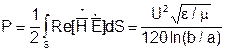Структура поля в коаксиальном волноводе:
 |