Круглый металлический волновод
Круглый металлический волновод это труба круглого сечения радиуса а из идеально проводящего металла бесконечно протяженная вдоль оси z.
Среда внутри – вакуум.
Качественно картину поля в круглом волноводе можно было бы получить деформируя прямоугольный волновод, причем волной низшего типа круглого волновода будет волна Н11. Для получения математического решения используем цилиндрическую систему координат (в дальнейшем ЦСК). Чтобы использовать ранее полученные результаты сделаем следующие преобразования:
Введем вектор
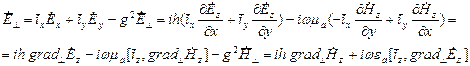(3.13)
Эти выражения позволяют определять поперечные составляющие через продольные в любой системе координат. При исследовании волн Н-типа следует исходить из уравнений Гельмгольца:
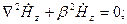
Воспользуемся выражением оператора Лапласа в ЦСК:
.
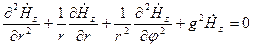Электрический вектор имеет касательную составляющую, которая должна обращаться в ноль на металле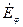 
(составляющая 
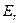отлична от нуля).
Тогда граничное условие принимает вид:
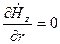при r = a.
Используем метод разделения переменных:
.
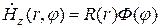После подстановки этого решения в уравнение Гельмгольца и деления его на произведение R и Ф получаем:
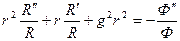(3.14)
Чтобы уравнение удовлетворялось при всех значениях r и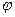 
обе части равенства должны быть равны некоторому постоянному числу. Например:
.
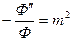Решение этого дифференциального уравнения второго порядка:
.
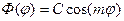Где С – произвольный постоянный коэффициент.
Т.к. волновод симметричен, то вместо функции cos можно использовать sin. Чтобы картина была периодична по углу φ с периодом 2π - m=0, 1, 2, … m – один из индексов волны Н – типа. Левая часть уравнения (3.14):
,
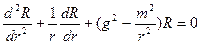в математике это уравнение хорошо изучено – Уравнение Бесселя. Его общее решение:
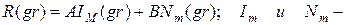Частные линейно независимые решения уравнения Бесселя.
Im - функция Бесселя или цилиндрическая функция первого рода порядка m.
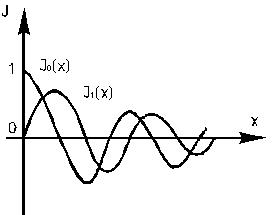
Nm+1 - функция Неймана или цилиндрическая функция второго рода порядка m. Роль этих функций в ЦСК такая же, как sin и cos в декартовой системе координат, но их вид значительно отличается от вида sin и cos.
Nm
 |
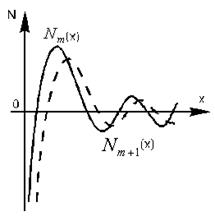+1 - функция Неймана или цилиндрическая функция второго рода порядка m. Роль этих функций в ЦСК такая же, как sin и cos в декартовой системе координат, но их вид значительно отличается от вида sin и cos.
1. Цилиндрические функции – непериодические
2. Их амплитуда уменьшается с ростом аргумента
3. При малых значениях аргумента(х→0) функции Nm неограниченно велики (Nm→-∞).
Для цилиндрических функций справедливы рекуррентные соотношения:
.
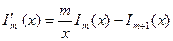Т.к. поле должно быть конечно в любой точке поперечного сечения волновода, то из физических соображений следует предположить В = 0. Обозначая произведение С и А через Н0 запишем амплитуду продольной проекции вектора Н:
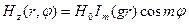(3.15)
Найдем из граничных условий поперечное волновое число g:
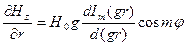
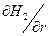будет равно 0 при r = a, если 
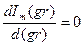при r = a.
Количество корней этого уравнения неограниченно, корни обозначают μmn, тогда:
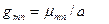(3.16)
и
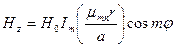(3.17)
Номер корня n – второй индекс волны.
Физический смысл индексов:
m – число вариаций поля по угловой координате,
n – характеризует изменение поля по координате r.
Каждой паре mn соответствует оригинальная картина поля в волноводе причем n≠0 (иначе Нz=0 или ∞). Критическая длина:
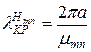(3.18)
 |
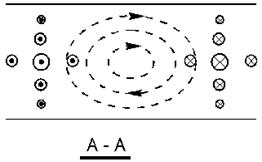Наименьшему корню производной функции Бесселя соответствует низший тип волны. Из графиков для Im следует, что низшим будет тип Н11(μ11=1,841). Структура совпадает с той, которую получили деформацией прямоугольного волновода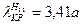 
.
 |
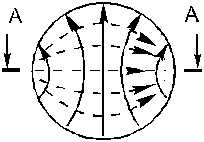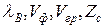определяются выражениями (3.5), (3.6), (3.7), (3.9), (3.10).
Правила, которые мы использовали при построении картин поля высших типов волн в прямоугольном волноводе, для круглого волновода не применимы.
Вывод выражений для волн Е типа аналогичен, но т.к. граничные условия для них Еz=0 при
r = a, то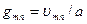 
, где υmn - корень уравнения Im(gr) = 0.
Низшей среди волн Е типа будет волна Е01 для нее υ01 = 2,405;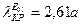 
.
Таблицы для μmn & υmn приведены в справочниках.
Выражение для продольной составляющей поля:
.
 |  | ||
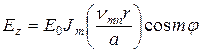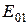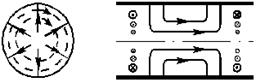Индекс m = 0 означает, что картина по φ - симметрична.
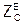определяется по (3.10).
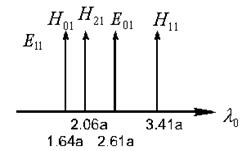
Построим диаграмму типов волн в круглом волноводе.
 |