Прямоугольный металлический волновод
 |
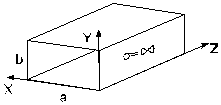Прямоугольный металлический волновод
| |
это полая металлическая идеально проводящая (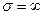 
) труба с поперечным сечением прямоугольной формы.
Будем полагать, что волновод заполнен средой с параметрами (воздух)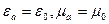 
. Найдем все типы электромагнитных волн, которые могут существовать внутри волновода на всем протяжении оси (как они созданы пока не рассматриваем).
Волны типа – H :
Для этих волн характерно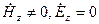 
. Тогда из системы (3.2):
; 
;
; 
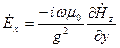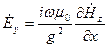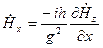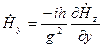(3.3)
Где функция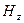 
является решением уравнения Гельмгольца ( 
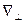- производные только по поперечным координатам):
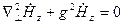, где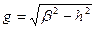 
и отыскивается в виде: 
.
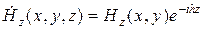При решении следует учитывать граничные условия (тангенциальная составляющая Е на металле обращается в 0):
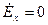при y = 0, y = b
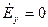при x = 0, x = а
При решении удобнее выразить их через :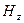
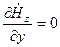при у = 0, у = b
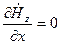при x = 0, x = а
Таким образом, надо решить краевую задачу Неймана (в ноль обращается производная, иначе Дирихле).
Используем метод Фурье, представляем 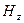в виде:
,
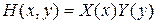подставляем его в уравнение Гельмгольца:
,
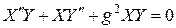разделим это уравнение на неизвестное решение:
.
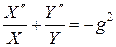g - не зависит от X и Y, поэтому, чтобы последнее уравнение выполнялось при всех X и Y, надо чтобы:
, 
,
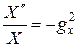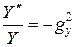где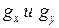 
- некоторые числа удовлетворяющие: 
.
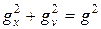Общие решения двух последних уравнений выражаются через гармонические функции:
;
.
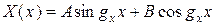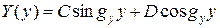Отсюда: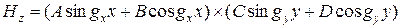 
.
Остается выбрать шесть величин A, B, C, D,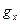 
, 
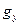так, чтобы выполнялись граничные условия на стенках волновода.
Граничные условия при X = 0 и Y = 0 будут выполнятся, если А = С = 0.
Произведение двух оставшихся амплитудных коэффициентов можно обозначить через H0 и тогда:
.
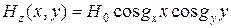Теперь остается подобрать величины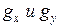 
так, чтобы граничные условия выполнялись при
X = а и Y = b:
; 
;
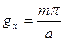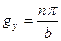Где m и n – любые целые положительные числа не равные нулю одновременно (иначе силовые линии магнитного поля Н - незамкнуты и нарушается четвертое уравнение Максвелла).
Краевая задача имеет решения отличные от нуля только при условии:
.
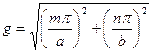Каждому значению g, (собственное значение) соответствует одно из множества решений уравнений Максвелла, которое в данном случае называют волнойHmn, где m и n – индексы волны данного типа. Физически они означают количества стоячих полуволн, возникающих внутри волновода вдоль координатных осей x и y соответственно.