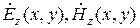Отражение от системы слоёв
На занятие решим задачу отражения от слоя.
Здесь приведём выражения для коэффициента отражения от системы слоёв.
Полагаем, что между двумя полубесконечными средами находится n – слоёв.
Коэффициент отражения: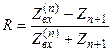 
где 
.
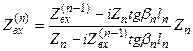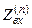- входной импеданс системы, причём, если угол падения не равен нулю, то следует использовать:
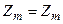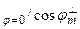
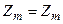ç 
ç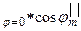 
при перпендикулярной и параллельной поляризациях соответственно.
Углы j рассчитывают исходя из законов Снелля.
УСВЧ
(Устройства сверх – высоких частот)
Классифицировать УСВЧ будем по функциям, которые они выполняют в линии передачи, независимо от того, для какой цели выполняется та или иная функция.
| Наименование класса устройств | Функциональные признаки |
| 1. Отрезки регулярных линий передач | Направленная передача ЭМЭ |
| 2. Соединительные устройства | Соединения отрезков регулярных линий, |
| А) Неподвижные и подвижные сочленения | элементов или узлов |
| Б) Уголки и изгибы | |
| В) Трансформаторы и фильтры типов волн | |
| Г) Вращающиеся сочленения | |
| 3. Делители мощности | Разделение энергии, передаваемой в одном канале, на несколько каналов или сложение энергии из нескольких каналов в одном |
| 4. Переключающие устройства (коммутаторы) | Временные соединения различных каналов |
| 5. Развязывающие устройства | Понижение уровня мощности, |
| А) Аттенюаторы | проходящей из одного канала в другой, |
| Б) Направленные ответвители | или полная развязка между каналами |
| В) Циркуляторы | |
| Г) Вентили | |
| 6.Поляризационные преобразователи | Преобразование поляризации проходящих волн |
| 7. Фазирующие устройства | Поддержание или изменение фазы или |
| А) Фазовращатели | разности фаз колебаний в линии |
| Б) Секции дифференциального Фазового сдвига | |
| 8. Мостовые (гибридные) соединения | Сложение, вычитание и калиброванное |
| А) Двойные Т-образные | разделение мощности ЭМВ в четырех |
| Б) Щелевые | канальном соединении |
| В) Кольцевые | |
| Г) Шлейфовые | |
| 9. Защитные устройства | Предохранение нагрузки или узла от чрезмерной мощности |
| 10. Согласующие устройства | Согласование тракта в целом его отдельных элементов и узлов для получения заданного коэффициента отражения |
| 11. Симметрирующие устройства | Переход от несимметричной линии или узла к симметричной линии или узлу. |
Линии передачи принято классифицировать по типу направляемых волн.
Типы волн:
1. Поперечные или волны Т-типа – отсутствуют составляющие E и Н, направленные вдоль направления распространения энергии (T-transfers (поперечные)) Т-(ТЕМ);
2. Электрические (Е- типа) Е-(ТМ);
3. Магнитные (Н-типа) Н-(ТЕ);
4. Смешанные (HE- типа) или гибридные.
Примеры этих волн – при отражение от границы раздела двух сред. Кроме того, все линии передачи делят на два больших класса:
1. Закрытого типа – вся энергия сосредоточенна в пространстве, ограниченном металлической оболочкой от внешней среды;
2. Открытого типа - поле, строго говоря, распределено во всем пространстве (подавляющая часть вблизи), поэтому параметры этих линий подвержены влиянию окружающей среды (метеоусловия, расположенные вблизи объекты и т.д.)
Связь между продольными и поперечными составляющими электромагнитного поля
Будем рассматривать производную, бесконечно длинную направляющую систему, ориентированную вдоль оси Z.
Будем полагать:
1. Форма поперечного сечения не зависит от Z - линия однородна, кроме того, параметры среды и граничные условия, которым удовлетворяют поля, не зависят от Z.
2. Направляющая система не вносит потерь.
Мы уже рассматривали направленные волны над границей раздела, характер изменения E и H вдоль продольных и поперечных координат был различным.
Введем два параметра:
1. Продольное волновое число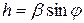 
.
2. Поперечное волновое число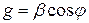 
т.е.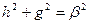 
.
Особенность направляемых волн: комплексная амплитуда каждой из шести проекций векторов Е и Н зависит от пространственных координат по закону:
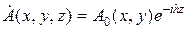
Начальную фазу волны всегда можно подобрать так, чтобы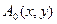 
- была действительной.
Производные по Z:
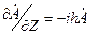(3.1)
Сторонние источники отсутствуют и поле описывается Уравнениями Максвелла:
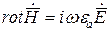
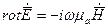
Развернем эти уравнения в декартовой системе координат. Из первого уравнения Максвелла:
;
;
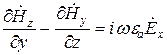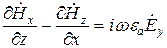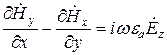
Из второго уравнения Максвелла:
;
;
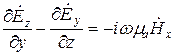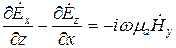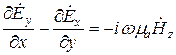
Решим эти уравнения относительно Е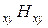 
(например, совместно первое и пятое уравнение):
; 
; 
; 
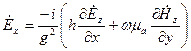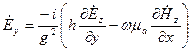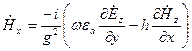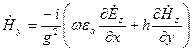(3.2)
Аналогично в любой другой системе координат.
Итак, достаточно найти лишь две функции для любой направляющей системы, а остальные проекции определяют через них 